Derivadas usando la definición | Introducción
Summary
TLDRThis video tutorial introduces the concept of derivatives, explaining their definition and application using practical examples. The instructor clarifies key terms like f(x+h) and demonstrates how to compute derivatives by applying the definition, including the process of factoring out 'h'. Students are guided through step-by-step examples, with tips on simplifying expressions. The video also offers practice exercises to reinforce understanding. With clear explanations and approachable examples, this tutorial makes learning derivatives accessible and easy to follow, encouraging viewers to further explore the topic through additional resources provided.
Please replace the link and try again.
Q & A
What is the definition of the derivative as explained in the video?
-The derivative is defined as the limit: lim(h → 0) [f(x+h) - f(x)] / h. This measures the rate of change of a function as the interval between x and x+h approaches zero.
Why does the instructor prefer using 'h' instead of 'Δx' in the derivative formula?
-The instructor prefers 'h' because it is simpler and less complicated compared to 'Δx', which is sometimes used in other textbooks.
How is the function f(x+h) calculated from the given f(x)?
-To calculate f(x+h), you substitute 'x+h' wherever 'x' appears in the function. For example, if f(x) = 3x + 2, then f(x+h) = 3(x+h) + 2.
What is the significance of the expression f(x+h) in derivative calculation?
-The expression f(x+h) is crucial because it allows us to evaluate the change in the function as the variable x changes by a small amount, h, which is key to finding the derivative.
In the example of f(x) = 3x + 2, how do you compute f(x+h)?
-For f(x) = 3x + 2, to compute f(x+h), you replace 'x' with 'x+h', resulting in f(x+h) = 3(x+h) + 2.
What is the process for factoring out 'h' in derivative problems?
-To factor out 'h', ensure that each term in the difference quotient contains an 'h'. For example, in the expression (f(x+h) - f(x)) / h, if there is an 'h' in the numerator, it can be factored out and canceled with the 'h' in the denominator.
What happens if 'h' cancels out completely in the derivative calculation?
-If 'h' cancels out completely, the result is 1. This often confuses students, but it is important to remember that this means the limit as h approaches zero simplifies to a constant value.
What are some common challenges students face when learning derivatives, as noted in the video?
-Students often struggle with understanding how to calculate f(x+h) and how to factor out 'h' correctly, especially when 'h' cancels out in the process.
How is factoring 'h' demonstrated with the function 2x^2 - 3x + 5?
-In the case of 2x^2 - 3x + 5, to calculate f(x+h), you replace x with x+h and then factor out 'h' from each term in the resulting expression. The steps involve simplifying and dividing terms by h where applicable.
What are the exercises mentioned in the video for practicing derivatives?
-The video provides exercises where students are asked to calculate f(x+h) for given functions and then factor out 'h'. These exercises help reinforce the steps and concepts covered in the video.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

KALKULUS | TURUNAN | APA ITU TURUNAN?

PENERAPAN TURUNAN DALAM TEKNIK SIPIL

ĐẠO HÀM và ý nghĩa hình học (Derivative Intro) | Vật Lý Chill
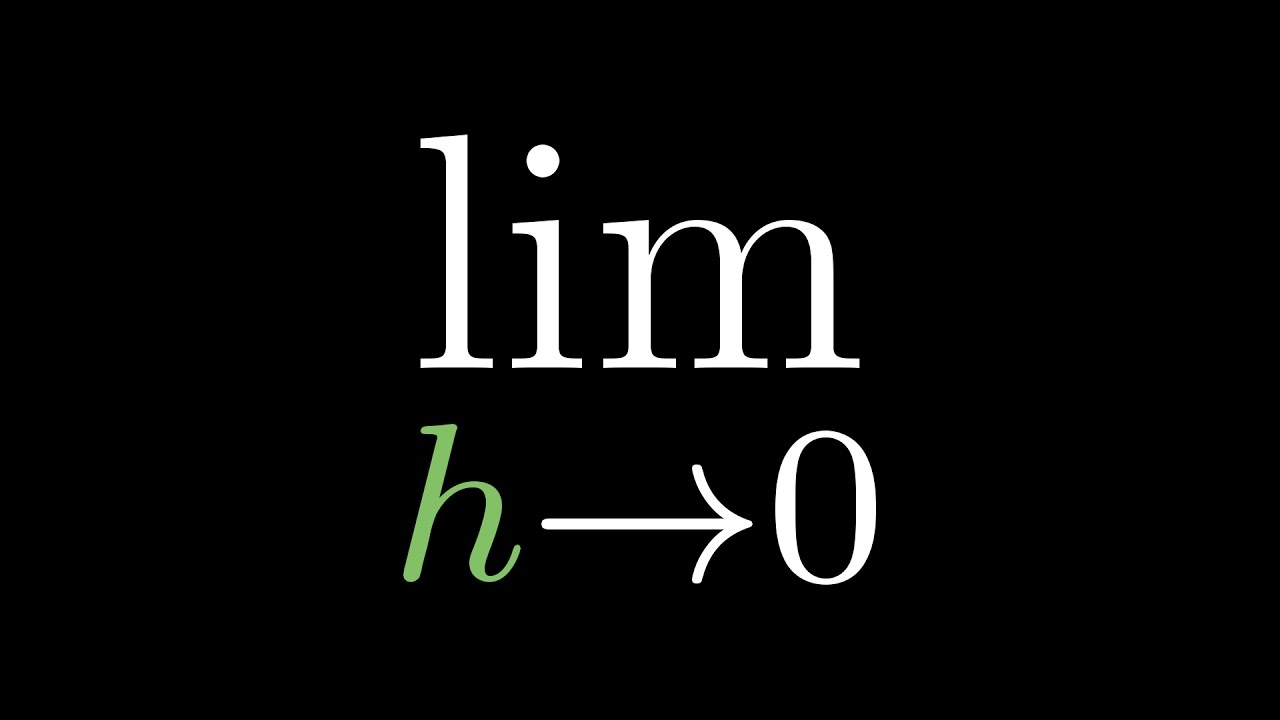
Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus

Yuk, Berpetualang di Dunia Algoritma SMP Kelas 9! | Materi Informatika Elemen Berpikir Komputasional

What are derivatives? - MoneyWeek Investment Tutorials
5.0 / 5 (0 votes)