Constructing an Ewald Sphere
Summary
TLDRThe video script delves into the fundamental principles of X-ray diffraction in crystallography, highlighting Bragg's Law and its significance in understanding how diffraction patterns are formed. It explains the concept of planes separated by a distance 'd' interacting with X-rays of wavelength 'lambda' and the conditions for diffraction to occur. The script introduces the idea of constructive and destructive interference leading to the appearance of spots in a diffraction pattern, indicative of 3D diffraction. The Ewald sphere model is presented as a more comprehensive 3D representation, illustrating how to construct the sphere, the role of crystal orientation, and the impact of varying the X-ray wavelength. The reciprocal space concept is used to redefine Bragg's Law, and the video concludes by demonstrating how changes in wavelength and crystal orientation can alter the accessible reflections, providing a deeper insight into the practical aspects of crystallography.
Takeaways
- 📐 **Bragg's Law in Crystallography**: Bragg's Law is fundamental for understanding how x-ray diffraction works in crystallography, relating the interplanar distance (d), the wavelength of x-rays (λ), and the diffracting angle (θ).
- 🌟 **Constructive and Destructive Interference**: In a diffraction experiment, constructive interference of x-rays leads to bright spots on the detector, while destructive interference results in no spots, forming a diffraction pattern.
- 📊 **3D Diffraction Pattern**: Diffraction is actually a 3D phenomenon, and the evolved sphere model helps to visualize and understand the 3D nature of diffraction spots.
- 🌐 **Reciprocal Space**: The concept of reciprocal space is introduced where each spot on the evolved sphere represents constructive interference and can be indexed with Miller indices (h k l).
- 🔬 **Radius of the Reflecting Sphere**: The radius of the reflecting or Ewald sphere in reciprocal space is inversely proportional to the wavelength of the x-rays (1/λ).
- 📉 **Effect of Wavelength on Diffraction**: Shorter wavelengths increase the radius of the reflecting and limiting spheres, allowing access to more reflections, whereas longer wavelengths result in smaller spheres.
- ⛓ **Lattice Planes and Reflections**: The arrangement and orientation of atoms in a crystal determine the reflections that can be harvested during a diffraction experiment.
- 🔄 **Crystal Rotation and Reflection Access**: Rotating the crystal allows for the collection of different reflections by changing the orientation of the lattice planes relative to the x-rays.
- 🔍 **Data Collection and Analysis**: The evolved sphere construction is essential for understanding how to collect data and which reflections are accessible at a given wavelength.
- 🛠️ **Crystallographic Techniques**: The script outlines the process of deriving Bragg's Law from both real and reciprocal space, providing a comprehensive view of diffraction analysis.
- 💡 **Practical Application**: The knowledge of Bragg's Law and the evolved sphere model is applied to grow and study crystals, highlighting the practical use of these theoretical concepts.
Q & A
What is Bragg's Law and how is it relevant in crystallography?
-Bragg's Law is a fundamental principle in X-ray crystallography that describes the conditions under which diffraction of X-rays occurs in a crystal lattice. It states that constructive interference of X-rays happens when the path difference between the rays reflected from successive planes of atoms is an integer multiple of the wavelength. Mathematically, it is represented as nλ = 2d * sin(θ), where n is an integer, λ is the wavelength of the X-rays, d is the interplanar spacing, and θ is the angle of incidence.
What is the significance of the term 'inter-planar distance' in Bragg's Law?
-The term 'inter-planar distance' refers to the distance between successive planes of atoms in a crystal lattice. It is crucial in Bragg's Law because diffraction occurs when this distance is of the same order as the wavelength of the X-rays. The inter-planar distance (d) determines the angles at which constructive interference will take place.
How does the concept of constructive and destructive interference relate to the appearance of spots in a diffraction pattern?
-In a diffraction experiment, the spots observed on the detector are a result of the interference of diffracted X-rays. Constructive interference, where the waves are in phase, leads to bright spots or reflections on the detector. Conversely, destructive interference, where the waves are out of phase, results in no spots or a reduction in intensity at those positions.
What is the evolved sphere and how does it improve the understanding of diffraction conditions in 3D?
-The evolved sphere is a 3D model that represents the conditions for X-ray diffraction more accurately than Bragg's Law, which is primarily a 2D representation. It is a conceptual tool that helps visualize the diffraction spots in three dimensions, similar to a sphere where each point on the surface represents a constructive interference from atoms in real 3D space. This model is particularly useful for understanding how to collect data and which reflections are accessible at a given wavelength.
What is the Miller index and how is it used in crystallography?
-The Miller index is a set of three integers (h, k, l) that denote the orientation of a crystal plane in a 3D lattice. It is used to label the spots observed on the evolved sphere, indicating how far the spot is from the origin along the reciprocal axes. The Miller indices are derived from the intercepts that the plane makes with the axes when extended to the origin.
How does the reciprocal space concept help in understanding Bragg's Law?
-Reciprocal space is a mathematical construct that helps in visualizing and understanding the diffraction pattern in a more intuitive way. In reciprocal space, the radius of the reflecting sphere is inversely proportional to the wavelength of the X-rays (1/λ), which allows for a clear understanding of how different wavelengths affect the accessible reflections and the resulting diffraction pattern.
What is the relationship between the wavelength of X-rays and the size of the reflecting and limiting spheres?
-The size of the reflecting and limiting spheres in reciprocal space is inversely proportional to the wavelength of the X-rays. A shorter wavelength results in larger spheres, which means more reflections are accessible. Conversely, a longer wavelength results in smaller spheres, limiting the number of accessible reflections.
How does the orientation of the crystal affect the reflections that can be harvested?
-The orientation of the crystal, or the lattice planes within it, determines which reflections will satisfy Bragg's Law and thus be observable. By rotating the crystal, different sets of lattice planes are brought into the correct orientation to diffract the X-rays, allowing for the observation of different reflections.
What is the significance of the angle θ in the context of Bragg's Law?
-The angle θ, known as the diffracting angle, is the angle between the incident X-ray beam and the plane of atoms in the crystal. It is a critical parameter in Bragg's Law as it determines the path difference between the X-rays reflected from successive planes of atoms, which in turn affects whether constructive or destructive interference will occur.
How does the choice of X-ray wavelength affect the outcome of a diffraction experiment?
-The choice of X-ray wavelength directly impacts the size of the reflecting and limiting spheres in reciprocal space, and thus the range of reflections that can be observed. A shorter wavelength allows for a larger sphere and more accessible reflections, potentially providing higher resolution data. A longer wavelength results in a smaller sphere and fewer accessible reflections.
What is the role of the detector in a diffraction experiment?
-The detector in a diffraction experiment is used to measure the intensity and position of the diffracted X-rays. It records the pattern of bright spots (constructive interference) and dark regions (destructive interference), which together form the diffraction pattern. This pattern is then analyzed to determine the structure of the crystal.
How does the concept of the evolved sphere help in the data collection process during a diffraction experiment?
-The evolved sphere provides a visual and conceptual framework for understanding which reflections are accessible at a given wavelength and crystal orientation. By rotating the crystal, different reflections come into the accessible region defined by the limiting sphere, allowing for systematic data collection and a more comprehensive understanding of the crystal structure.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
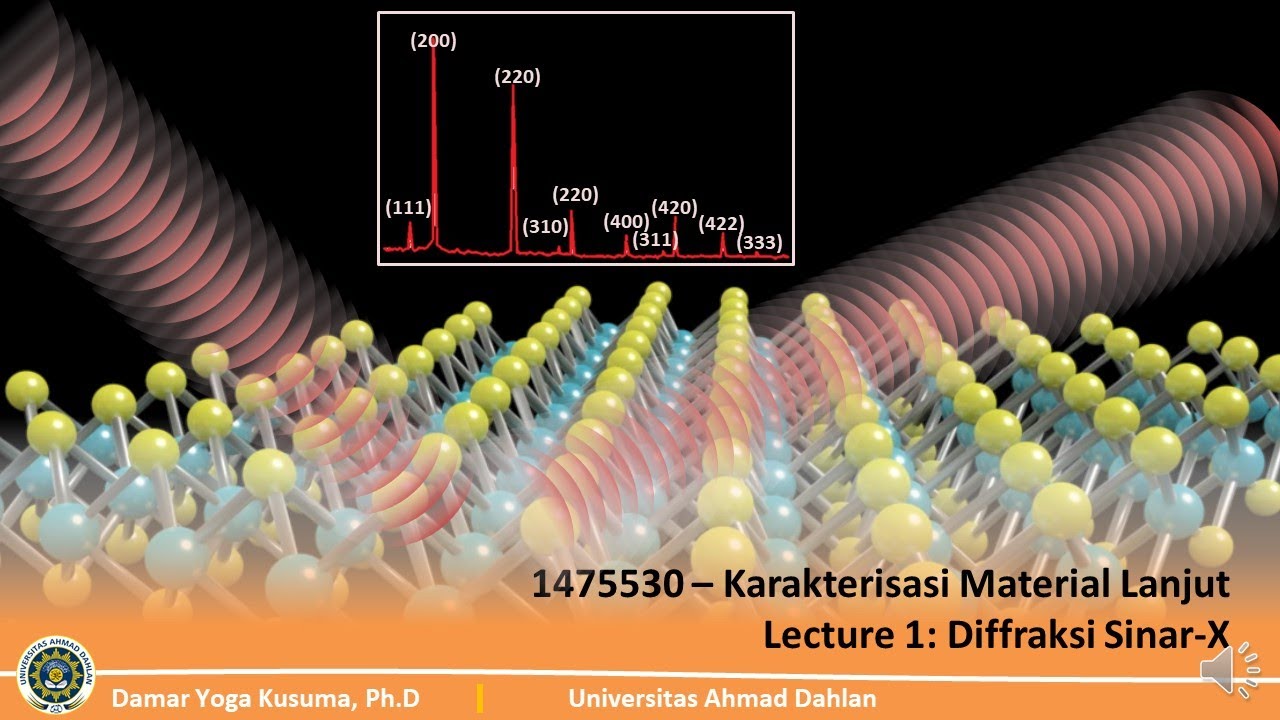
UAD - Kuliah Online 1475530 Karakterisasi Material Lanjut (Lecture 1b)
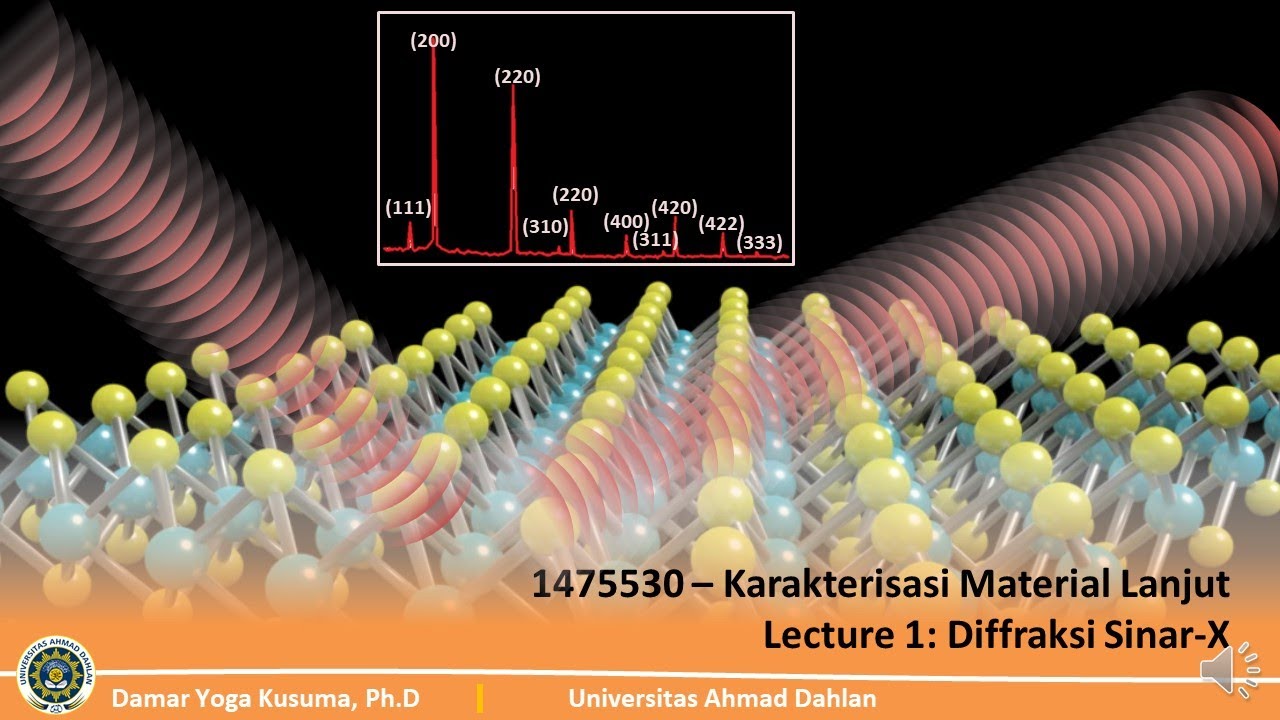
UAD - Kuliah Online 1475530 Karakterisasi Material Lanjut (Lecture 1c)
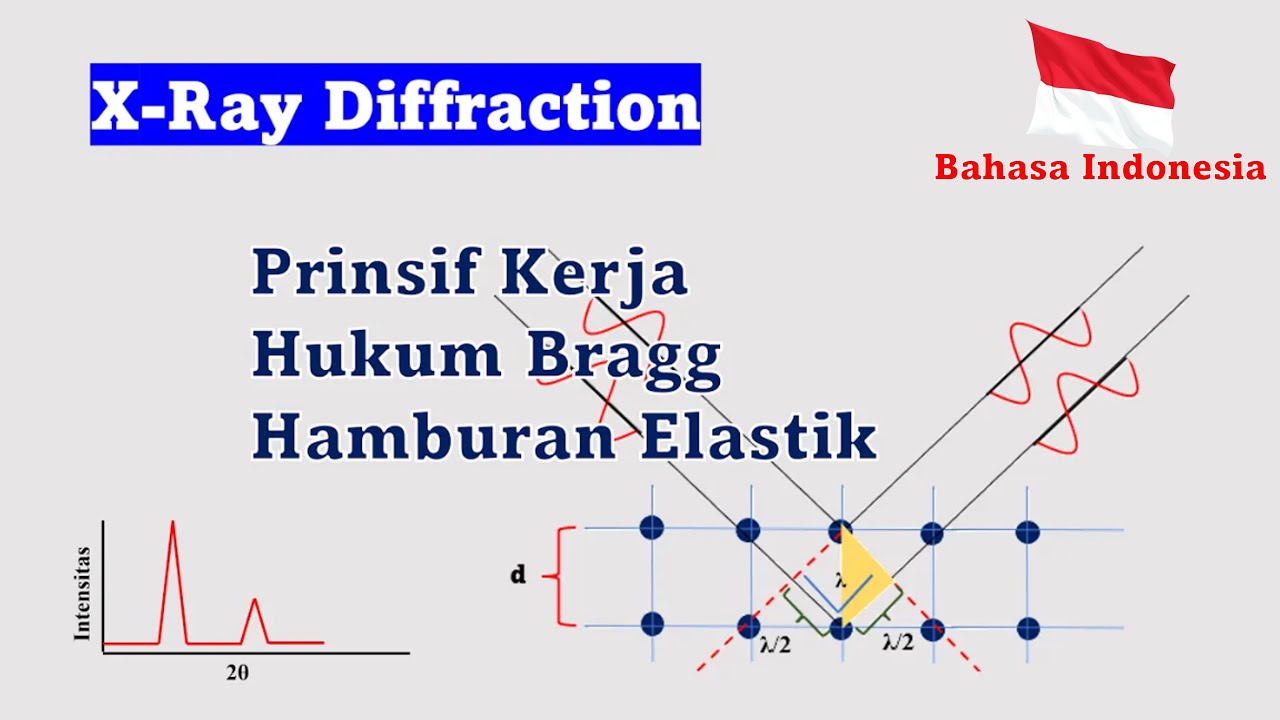
Prinsip Kerja XRD (X-Ray Diffraction) | Hukum Bragg | Bahasa Indonesia

4B Planos cristalográficos - Difração de Raios X

Mineralogi Petrografi - Acara 8 - Pengenalan XRD, XRF, dan SEM

X ray crystallography basics explained | x ray diffraction
5.0 / 5 (0 votes)