Physics 10 Momentum and Impulse (5 of 30) Why you Don't Want to Collide with a Semi Truck
Summary
TLDRThis video explains the physics concepts of momentum and impulse, focusing on a problem involving a collision between a car and a truck. It distinguishes between elastic and inelastic collisions, highlighting that in inelastic collisions, objects stick together, losing energy. The speaker walks through a step-by-step calculation of the final velocity after a collision, where a 1,000 kg car moving east collides with a 50,000 kg truck moving west. The explanation emphasizes the principle of momentum conservation and how direction influences calculations. The final outcome is a shared velocity of -9 m/s to the left.
Takeaways
- 🔍 Momentum and impulse are closely related topics in physics.
- 🚗 The problem involves a 1,000 kg car moving east at 30 m/s colliding with a 50,000 kg truck moving west at 20 m/s.
- 🔗 Since the car gets stuck on the truck after collision, this is classified as an inelastic collision, meaning energy is lost and the two move together afterward.
- 📉 In an inelastic collision, the final momentum is conserved and equals the total momentum of both objects before the collision.
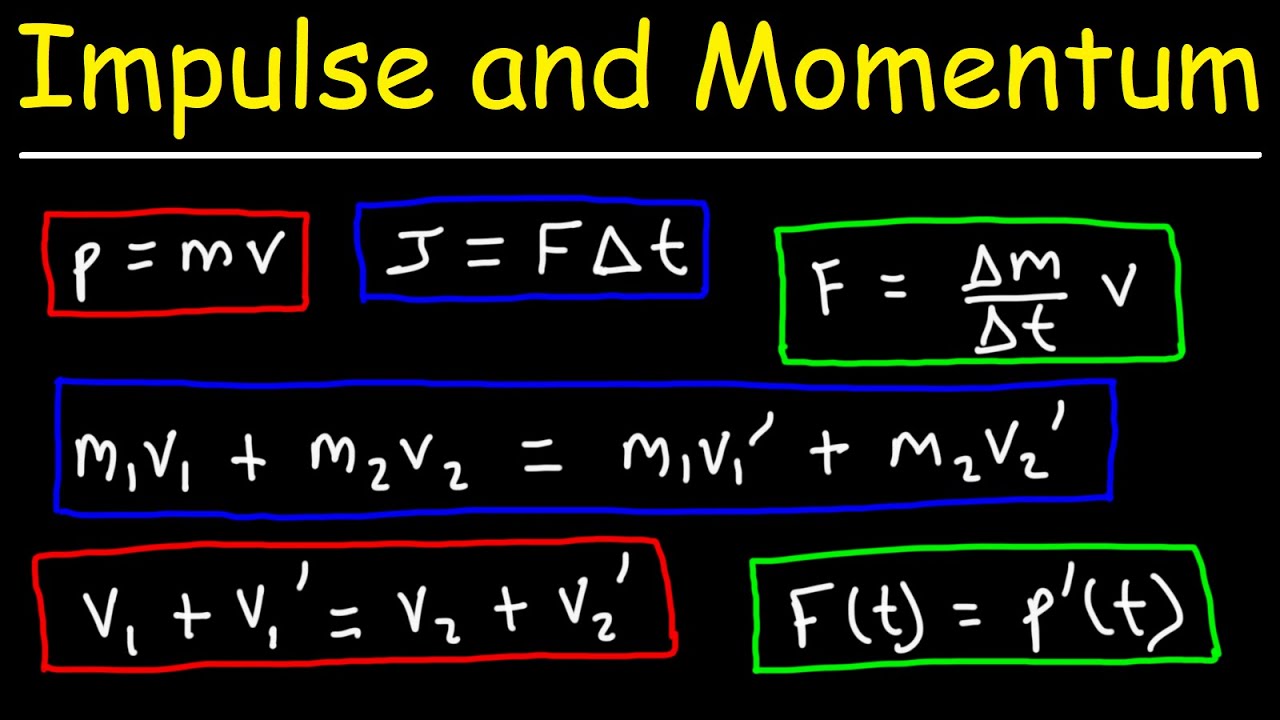
- 📐 Momentum is calculated using the formula: mass times velocity.
- ➡️ Direction is crucial in momentum problems, with east (right) considered positive and west (left) negative.
- 🔢 The final velocity of the truck and car together can be calculated using momentum conservation: (M_car * V_car_initial) + (M_truck * V_truck_initial) = (M_car + M_truck) * V_final.
- 🧮 After plugging in the numbers, the final velocity of the combined car and truck is calculated to be -9 m/s, indicating they are moving left (west).
- 💡 The collision slowed the truck down slightly, but it still moves westward due to its larger mass.
- 📊 Momentum is always conserved in collisions, making it a key principle in determining the final velocity in such problems.
Q & A
What are the two types of collisions discussed in the script?
-The script discusses two types of collisions: elastic collisions and inelastic collisions. Elastic collisions are those where the two objects hit and stick together, and no energy is lost. Inelastic collisions are those where the two objects collide and bounce back, moving independently after the collision, and energy is lost.
What is the difference between momentum and impulse?
-The script does not explicitly differentiate between momentum and impulse. However, in physics, momentum is the product of an object's mass and velocity and is a vector quantity, while impulse is the change in momentum of an object and is equal to the force applied over the time interval during which it acts.
Why is the collision between the car and the truck considered an inelastic collision?
-The collision is considered inelastic because the car becomes stuck on the front of the truck after they collide, indicating that a significant amount of energy is lost during the collision and they move together afterward.
How is the final velocity of the truck and car after the collision determined?
-The final velocity is determined by the principle of conservation of momentum. The total momentum before the collision (sum of the momenta of the car and the truck) is equal to the total momentum after the collision (momentum of the car and truck stuck together).
What is the formula for calculating the final velocity of the truck and car after the collision?
-The formula for calculating the final velocity (V_final) is: (M * V_initial_car + M_big * V_initial_truck) / (M + M_big), where M is the mass of the car, V_initial_car is the initial velocity of the car, M_big is the mass of the truck, and V_initial_truck is the initial velocity of the truck.
In which direction will the truck and car move after the collision?
-After the collision, the truck and car will move to the left, which is the direction the truck was initially moving before the collision.
What is the initial momentum of the car and the truck before the collision?
-The initial momentum of the car is its mass (1000 kg) times its velocity (30 m/s), which is a positive value because it's moving to the right (East). The initial momentum of the truck is its mass (50000 kg) times its velocity (-20 m/s), which is a negative value because it's moving to the left (West).
Why is the truck's initial velocity considered negative in the calculation?
-The truck's initial velocity is considered negative because it is moving to the left (West), which is the opposite direction of the positive direction (East) chosen for the car's velocity.
What is the final velocity of the truck and car after the collision?
-The final velocity of the truck and car after the collision is -9 m/s, indicating they move to the left (West) at 9 m/s.
Why is it easier to solve for the final velocity when the collision is inelastic?
-It is easier to solve for the final velocity in an inelastic collision because the two objects stick together after the collision, so they share the same final velocity, simplifying the calculation.
What is the significance of the negative sign in the final velocity value?
-The negative sign in the final velocity value indicates the direction of motion, which is to the left (West). The magnitude of the velocity is 9 m/s.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

FISIKA KELAS X | MOMENTUM, IMPULS, dan TUMBUKAN (PART 2) - Hukum Kekekalan Momentum

Fisika SMA - Impuls & Momentum (2) - Hubungan antara Impuls dan Momentum (I)

Introduction to momentum | Impacts and linear momentum | Physics | Khan Academy
Impulse and Momentum - Formulas and Equations - College Physics

FISIKA SMA/SMK, TUMBUKAN LENTING SEMPURNA, LENTING SEBAGIAN, TIDAK LENTING SAMA SEKALI
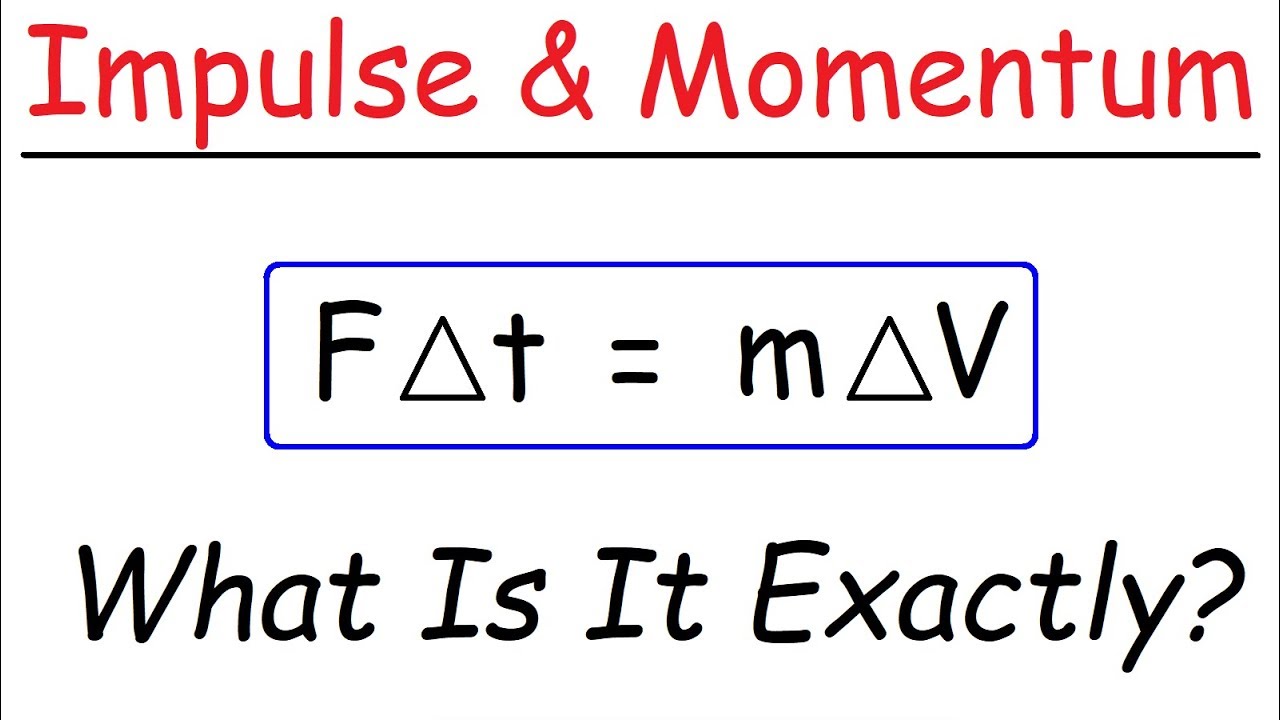
Introduction to Impulse & Momentum - Physics
5.0 / 5 (0 votes)