Impulse and Momentum - Formulas and Equations - College Physics
Summary
TLDRThis video offers a concise review of impulse and momentum, essential for mastering physics exams. It covers key formulas, including momentum as mass times velocity and impulse as force times time. The video explains the relationship between impulse and change in momentum, Newton's Second Law, and how to calculate force exerted by a fluid. It also delves into conservation of momentum, differentiating between elastic and inelastic collisions, and provides equations for solving collision problems, making it an informative resource for students.
Takeaways
- 📚 The first key formula is momentum, which is calculated as mass times velocity (p = mv).
- 📐 Momentum is a vector quantity, meaning both magnitude and direction are important.
- 🔨 Impulse is the product of force and the time over which it acts (I = F * t), and it represents the total force applied over a time period.
- 🔄 Impulse is equal to the change in momentum (I = Δp), which is derived from Newton's second law and the relationship between force, mass, and acceleration.
- 🚀 An example of calculating impulse involves applying a force of 100 Newtons for 8 seconds, resulting in an impulse of 800 Newton-seconds.
- 💧 The force exerted by a fluid can be calculated using the mass flow rate and the velocity of the fluid (F = mass flow rate * v).
- 📉 Force can also be described as the rate of change of momentum with respect to time, which is the derivative of the momentum function (F(t) = d(p)/dt).
- 💥 In inelastic collisions, only momentum is conserved, not kinetic energy, and objects involved in the collision stick together.
- 🔄 The conservation of momentum formula states that the total momentum before a collision equals the total momentum after the collision, assuming no external forces (p_initial = p_final).
- 🧩 For inelastic collisions where objects stick together, the conservation of momentum simplifies to the total mass times the final velocity (M1 + M2) * Vf.
- 🏀 In elastic collisions, both momentum and kinetic energy are conserved, and the final speeds of the objects can be found using the conservation of momentum and energy equations.
Q & A
What is the formula for momentum?
-Momentum is calculated as mass times velocity (p = mv). Momentum is a vector, where mass is a scalar and velocity is a vector.
How do you calculate the momentum of a 10 kg block moving at 6 m/s?
-The momentum of a 10 kg block moving at 6 m/s is calculated as: momentum = mass * velocity = 10 kg * 6 m/s = 60 kg·m/s.
What is impulse and how is it calculated?
-Impulse is the product of force and the time over which the force is applied. It is calculated as: impulse (J) = force (F) * time (Δt).
If a force of 100 Newtons is applied for 8 seconds, what is the impulse imparted to an object?
-The impulse imparted to an object is calculated as: impulse = force * time = 100 Newtons * 8 seconds = 800 Newton·seconds.
How are impulse and momentum related?
-Impulse is equal to the change in momentum. This relationship is derived from Newton's Second Law, where force is equal to mass times acceleration, and acceleration is the change in velocity over time.
What is the impulse-momentum theorem?
-The impulse-momentum theorem states that the impulse on an object is equal to the change in its momentum, expressed as: FΔt = mΔv.
How can you calculate the force exerted by a fluid on an object using mass flow rate?
-Force can be calculated using the mass flow rate and velocity of the fluid: force = mass flow rate (Δm/Δt) * velocity (v).
What is the derivative form of the force in terms of momentum for those taking calculus with physics?
-For calculus students, force can be described as the rate at which momentum changes with respect to time: F(t) = d(p)/dt, where p is momentum.
What is the principle of conservation of momentum?
-The principle of conservation of momentum states that the total momentum of a system remains constant if no external forces are acting on it. This is expressed as: total momentum before collision = total momentum after collision.
How is momentum conserved in inelastic collisions?
-In inelastic collisions, momentum is conserved but kinetic energy is not. When two objects collide and stick together, the total momentum before collision equals the total momentum after collision: m1v1 + m2v2 = (m1 + m2)vf.
What additional equation is needed to solve for velocities in a perfectly elastic collision?
-In a perfectly elastic collision, both momentum and kinetic energy are conserved. The additional equation used is: v1 + v1' = v2 + v2', where v1 and v2 are initial velocities, and v1' and v2' are final velocities.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

08 01 Fisika Dasar 1- Momentum Dan Impuls

FISIKA Kelas 10 - Momentum & Impuls | GIA Academy

Penerapan Momentum dan Impuls dalam Kehidupan Sehari-hari - Fisika - Santri Asshiddiqiyah

Fisika SMA - Impuls & Momentum (1) - Pengenalan Impuls dan Momentum, Rumus Impuls dan Momentum (I)
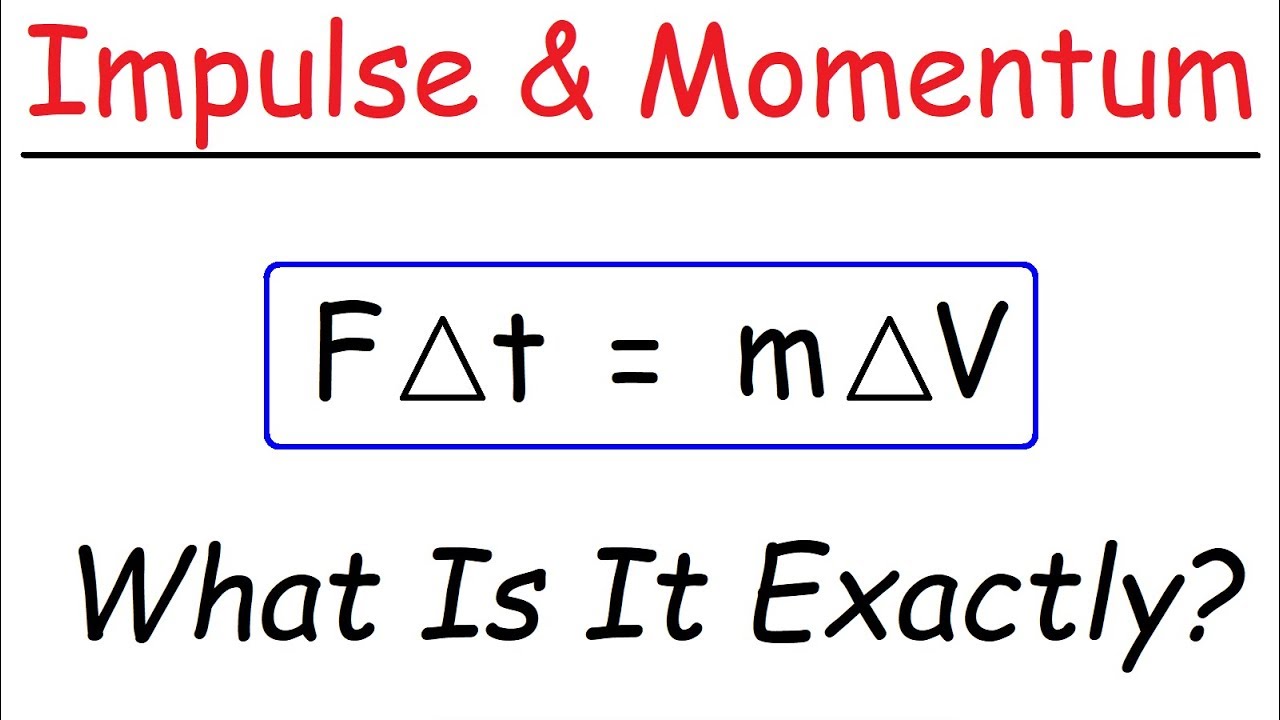
Introduction to Impulse & Momentum - Physics

Lesson 11 - Momentum And Impulse in Physics
5.0 / 5 (0 votes)