3.3. Parametrización de superficies

MATEMATICAS-UNAQ

6 Nov 202019:40

Summary

TLDREl script proporciona una introducción a la parametrización de superficies en geometría diferencial. Se define una superficie paramétrica como una que puede ser representada por una función gamma que mapea un dominio en R^2 a la superficie en R^3. Se discuten las ecuaciones paramétricas y la importancia de las derivadas parciales en un punto dado. Luego, se presentan ejemplos de parametrización para una esfera y un cilindro, y se justifica la elección de los rangos para los parámetros en función de las coordenadas esféricas. Además, se aborda la parametrización de superficies de revolución, destacando cómo se puede obtener a partir de funciones continuas y no negativas. Se ilustra con un ejemplo la parametrización de la parte superior de una esfera centrada en el origen con radio r, utilizando una función escalar. El script es una guía valiosa para comprender conceptos fundamentales en geometría diferencial y su aplicación en la parametrización de figuras geométricas comunes.

Takeaways

📐 Una superficie en R³ es paramétrica si existe una función gamma que mapea un dominio en R² a la superficie.
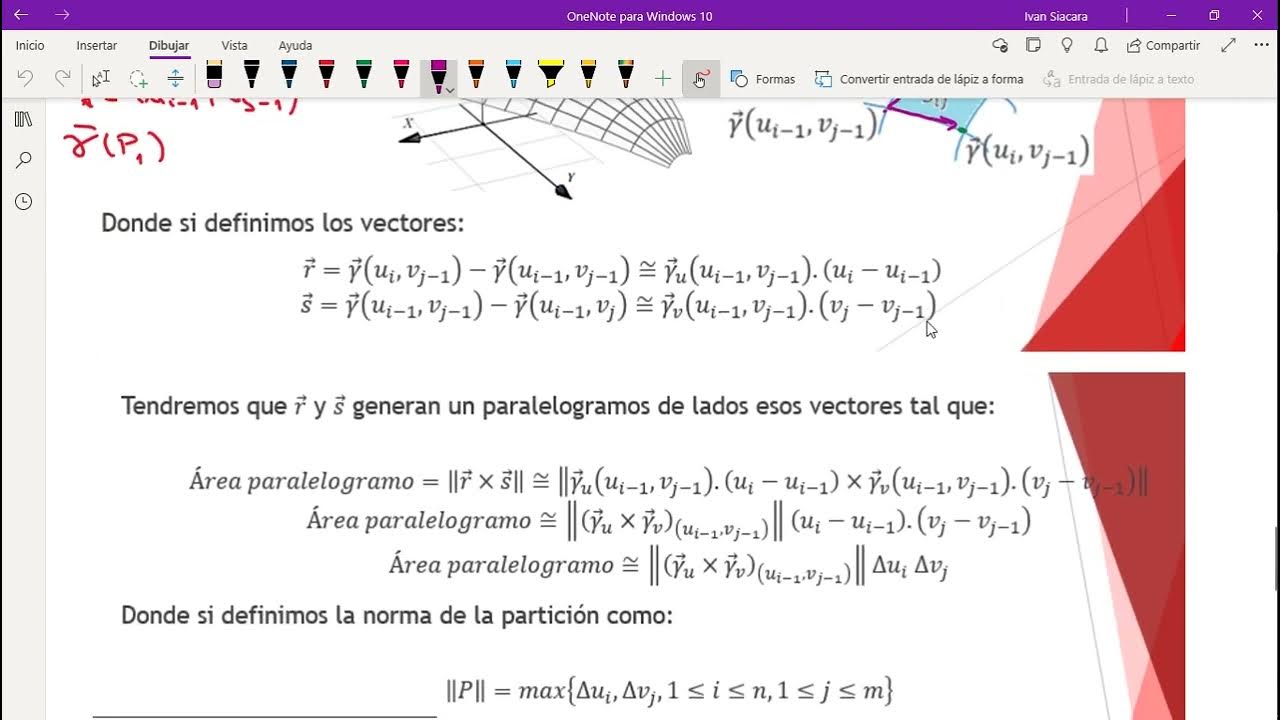
🔍 La parametrización de una superficie es análoga a la parametrización de curvas, y generalmente se expresa en las coordenadas x(u, v), y(u, v), z(u, v).
🌐 Se puede parametrizar una esfera de radio r centrada en el origen usando la función vectorial r * (seno(theta) * cos(phi), seno(theta) * sin(phi), cos(theta)), con theta y phi variando en intervalos específicos.
📏 Las derivadas parciales de gamma son importantes para entender la tangente a la superficie en un punto dado.
🛰️ Las coordenadas esféricas son útiles para parametrizar figuras como esferas, donde r representa el radio, theta la longitud y phi la latitud.
🔄 Una superficie de revolución se puede generar girando una función continua y no negativa alrededor del eje z.
📏 Una parametrización de un cilindro puede ser dada por x(r, theta) = (r * cos(theta), r * sin(theta), s), donde s es la altura y theta varía entre 0 y 2*pi.
📈 La superficie generada por un campo escalar en R², como la parte superior de una esfera, puede ser parametrizada usando la gráfica del campo escalar y su dominio.
🔧 Las derivadas parciales son fundamentales para calcular la matriz jacobiana, que describe cómo se transforman las áreas locales en la superficie parametrizada.
🧮 La parametrización de superficies permite la realización de cálculos en geometría diferencial, incluyendo el cálculo de曲率 (curvatura) y la torsión (torque) de la superficie.
🌟 Una parametrización adecuada de una superficie permite visualizar y manipular la superficie de manera más sencilla en aplicaciones como modelado 3D y análisis de superficies.

Q & A

¿Qué es una superficie paramétrica?
-Una superficie paramétrica es una superficie en R³ que se puede describir a través de una función γ que mapea un dominio Ω en R² a la superficie S. Esta función es conocida como parametrización de la superficie.
¿Cómo se definen las ecuaciones paramétricas para una superficie?
-Las ecuaciones paramétricas para una superficie se definen como x = f(u, v), y = g(u, v), z = h(u, v), donde (u, v) son coordenadas en el dominio de la parametrización y x, y, z son coordenadas en R³.
¿Por qué las derivadas parciales son importantes en la parametrización de superficies?
-Las derivadas parciales son importantes porque nos permiten encontrar los vectores tangentes a la superficie en un punto dado, lo que es fundamental para estudiar propiedades como la curvatura o la inclinación de la superficie en ese punto.
¿Cómo se parametriza una esfera de radio r centrada en el origen?
-Una esfera de radio r centrada en el origen se puede parametrizar usando la función vectorial γ(r, θ, φ) = (r * sen(θ) * cos(φ), r * sen(θ) * sin(φ), r * cos(θ)), donde r varía en el intervalo [0, r], θ en [0, π] y φ en [0, 2π].
¿Cómo se justifica el rango de los parámetros θ y φ para la parametrización de una esfera?
-El rango de los parámetros θ y φ se justifica porque representan ángulos en un sistema de coordenadas esféricas. θ varía de 0 a π para abarcar todos los ángulos desde el polo norte hasta el polo sur, y φ varía de 0 a 2π para abarcar todos los ángulos en el plano horizontal.
¿Cómo se relacionan las coordenadas esféricas con las coordenadas cartesianas en una parametrización?
-Las coordenadas esféricas (r, θ, φ) se relacionan con las coordenadas cartesianas (x, y, z) a través de las ecuaciones x = r * sen(θ) * cos(φ), y = r * sen(θ) * sin(φ), z = r * cos(θ).
¿Cómo se parametriza un cilindro acostado sobre el eje de las z?
-Un cilindro acostado sobre el eje de las z se puede parametrizar usando la función γ(r, φ, s) = (r * cos(φ), r * sin(φ), s), donde r es el radio del cilindro, φ varía en [0, 2π] para representar la circunferencia transversal y s varía en un intervalo [0, h] que representa la altura en el cilindro.
¿Cómo se parametriza una superficie de revolución generada por una función continua y no negativa?
-Una superficie de revolución generada por una función continua y no negativa se parametriza variando el radio de las circunferencias transversales según la evaluación de la función en cada punto. La parametrización general es de la forma γ(s, φ) = (f(s) * cos(φ), f(s) * sin(φ), s), donde s es la coordenada longitudinal y φ varía en [0, 2π] para la circunferencia.
¿Cómo se relaciona la parametrización de una superficie de revolución con la gráfica de un campo escalar en R²?
-La parametrización de una superficie de revolución está relacionada con la gráfica de un campo escalar en R² porque la superficie de revolución se obtiene girando la gráfica del campo escalar alrededor de un eje. El dominio de la parametrización corresponde a la región en el plano R² que proyecta la sombra de la gráfica sobre el eje de rotación.
¿Cómo se parametriza la parte superior de una esfera de radio r centrada en el origen?
-La parte superior de una esfera de radio r se parametriza usando la función γ(s, φ) = (sqrt(r^2 - s^2) * cos(φ), sqrt(r^2 - s^2) * sin(φ), s), donde s varía en el intervalo [0, r] y φ varía en [0, 2π].
¿Cómo se determina el dominio de la parametrización para la parte superior de una esfera?
-El dominio de la parametrización para la parte superior de una esfera se determina como el conjunto de pares ordenados (s, φ) tales que s^2 + φ^2 ≤ r^2, lo que corresponde a la sombra proyectada de la parte superior de la esfera en el plano.

Outlines

00:00

😀 Introducción a la Parametrización de Superficies

Este primer párrafo introduce la parametrización de superficies en el espacio tridimensional. Se define una superficie paramétrica como una función gamma que mapea un dominio en el plano R^2 a la superficie en R^3. La parametrización es esencial para el estudio de curvas en R^3 y se utiliza para representar la superficie de objetos geométricos complejos como esferas y cilindros. Se proporciona un ejemplo de parametrización de una esfera, usando funciones vectoriales y mostrando cómo las ecuaciones paramétricas se relacionan con la ecuación de una esfera de radio r.

05:02

📐 Parametrización de un Cilindro y Superficies de Revolución

El segundo párrafo se enfoca en la parametrización de un cilindro yacída sobre el eje de las zetas. Se describe cómo se puede parametrizar una circunferencia en un corte transversal del cilindro y cómo las coordenadas de la parametrización representan diferentes partes del cilindro. Además, se explora la parametrización de superficies de revolución generadas por una función continua y no negativa, y se da un ejemplo de cómo parametrizar una esfera usando una función que involucra la raíz cuadrada de la diferencia de los cuadrados de las coordenadas x e y.

10:05

🌐 Parametrización de una Superficie de Revolución

Este párrafo profundiza en la parametrización de superficies de revolución, que son superficies generadas por la rotación de una curva en torno a un eje. Se discute cómo las circunferencias generadas por los cortes transversales varían en tamaño dependiendo de la posición en el eje. Se proporciona una parametrización detallada para una superficie de revolución, incluyendo la forma en que se eligen los parámetros para representar las coordenadas en el espacio tridimensional. Se utiliza como ejemplo la parametrización de la parte superior de una esfera, mostrando cómo se puede obtener a partir de una función escalar y su dominio de definición.

15:06

🔍 Parametrización de la Parte Superior de una Esfera

El cuarto y último párrafo se centra en la parametrización específica de la parte superior de una esfera centrada en el origen con un radio dado. Se describe el proceso de generación de la superficie a partir de la gráfica de un campo escalar, y cómo se puede obtener la parte superior de la esfera tomando el signo positivo de la función escalar. Se proporciona una fórmula de parametrización para esta superficie, incluyendo el rango de valores que toman los parámetros y cómo se relacionan con el dominio de la función escalar en el plano xy.

Mindmap

Keywords

💡Parametrización

La parametrización es el proceso de representar una superficie o curva en el espacio mediante una función que mapea un dominio en dos dimensiones (generalmente un rectángulo en el plano) a un punto en el espacio tridimensional. En el video, se utiliza la parametrización para describir formas geométricas complejas como esferas y cilindros, permitiendo entender sus propiedades a través de funciones matemáticas.

💡Superficie paramétrica

Una superficie paramétrica es aquella que se define mediante una función vectorial que toma dos parámetros y devuelve un punto en el espacio tridimensional. En el contexto del video, las superficies paramétricas son fundamentales para la representación de figuras geométricas como la esfera y el cilindro, mostrando cómo se pueden construir a partir de funciones matemáticas.

💡Ecuaciones paramétricas

Las ecuaciones paramétricas son una forma de describir la geometría de una curva o superficie utilizando una o más funciones paramétricas. Estas ecuaciones expresan las coordenadas de un punto en la curva o superficie en términos de un parámetro. En el video, las ecuaciones paramétricas son utilizadas para definir la forma de una esfera y un cilindro.

💡Esfera

Una esfera es una superficie geométrica perfectamente redonda en todos los sentidos, generalmente definida como el conjunto de todos los puntos en el espacio que están a una distancia fija de un punto central. En el video, se muestra cómo parametrizar una esfera de radio r centrada en el origen, usando funciones trigonométricas.

💡Cilindro

Un cilindro es una superficie geométrica que extiende una circunferencia a lo largo de una distancia finita formando una figura tridimensional. En el video, se discute cómo parametrizar un cilindro, destacando que puede ser visto como una superficie generada por la rotación de una circunferencia alrededor de un eje.

💡Superficie de revolución

Una superficie de revolución es aquella que se forma al girar una curva en torno a un eje. Este concepto es central en el video, donde se explica cómo parametrizar superficies que resultan de revoluciones, como la parte superior de una esfera, a partir de funciones definidas en un dominio en el plano.

💡Campo escalar

Un campo escalar es una asignación de un único valor escalar a cada punto de un dominio en el espacio. En el video, se menciona el uso de campos escalares para definir gráficas que, cuando son revolvidas alrededor de un eje, generan superficies de revolución, como la parte superior de una esfera.

💡Coordenadas esféricas

Las coordenadas esféricas son un sistema de coordenadas en el que se describe la posición de un punto en el espacio tridimensional utilizando dos ángulos (azimut y elevación) y una distancia al origen. En el video, se utiliza el concepto de coordenadas esféricas para parametrizar una esfera.

💡Derivadas parciales

Las derivadas parciales son utilizadas en matemáticas para medir cómo una función de varias variables cambia en una dirección específica mientras se mantienen las demás variables constantes. En el video, se alude a las derivadas parciales como una herramienta para estudiar las propiedades de las superficies paramétricas.

💡Dominio

El dominio de una función es el conjunto de todos los valores posibles de entrada (o argumentos) para los cuales la función está definida. En el video, el dominio es crucial para definir las restricciones sobre los valores que pueden tomar los parámetros en una parametrización.

💡Rectángulo en el plano

Un rectángulo en el plano es una figura geométrica definida por dos pares de paralelas perpendiculares. En el contexto del video, los rectángulos en el plano son utilizados para representar el dominio de las funciones paramétricas que definen superficies en el espacio tridimensional.

Highlights

Definición de una superficie paramétrica como una función gamma que mapea un dominio en R^2 a la superficie S en R^3.

La parametrización de la superficie S es análoga a la parametrización de curvas en geometría diferencial.

Las ecuaciones paramétricas generales para una superficie en R^3 son x = x(u, v), y = y(u, v), z = z(u, v).

La existencia de derivadas parciales de x, y, z es fundamental para la parametrización de superficies.

Ejemplo de parametrización de una esfera con radio r centrada en el origen usando funciones trigonométricas.

Las ecuaciones paramétricas para la esfera son x = r * sin(θ) * cos(φ), y = r * sin(θ) * sin(φ), z = r * cos(θ).

La elección del dominio para la parametrización de la esfera está relacionada con las coordenadas esféricas.

La parametrización de un cilindro yaciendo sobre el eje z usando dos parámetros, uno para la altura y otro para la circunferencia.

La superficie de revolución se puede parametrizar a partir de una función definida en un intervalo cerrado.

La parametrización de una superficie de revolución involucra dos parámetros y una coordenada adicional para la circunferencia.

Ejemplo de parametrización de la parte superior de una esfera a través de una función escalar en R^2.

La esfera puede ser vista como una superficie de revolución generada por la gráfica de una función escalar.

La parametrización de la superficie superior de una esfera implica la elección de un campo escalar y su dominio apropiados.

La parametrización de una superficie de revolución puede ser utilizada para representar tanto la parte superior como la inferior de una esfera.

La parametrización de una superficie de revolución es una herramienta poderosa para estudiar propiedades de superficies complejas.

La parametrización permite la transformación de coordenadas rectangulares en coordenadas esféricas para superficies como cilindros y esferas.

La elección del dominio omega es crucial para la parametrización adecuada de superficies de revolución.