3.4. Área de una superficie

Summary

El script proporcionado es una lección avanzada de geometría diferencial que explora la parametrización de superficies en R³ y su aplicación para calcular áreas. Se discute la definición del producto vectorial fundamental y su importancia para encontrar el vector normal a una superficie en un punto dado. A lo largo del script, seguidamente se calcula el área de diferentes superficies, incluyendo una esfera y un toro, utilizando distintas parametrizaciones. Se destaca la relevancia de la elección adecuada de la parametrización para simplificar los cálculos. Finalmente, se resalta que el área de una superficie es invariante ante diferentes parametrizaciones, lo cual es un concepto clave en el análisis de superficies en geometría diferencial.

Takeaways

• 📐 La parametrización de una superficie en R³ permite definir vectores tangentes a las curvas sobre la superficie y un vector normal a la superficie en un punto dado.
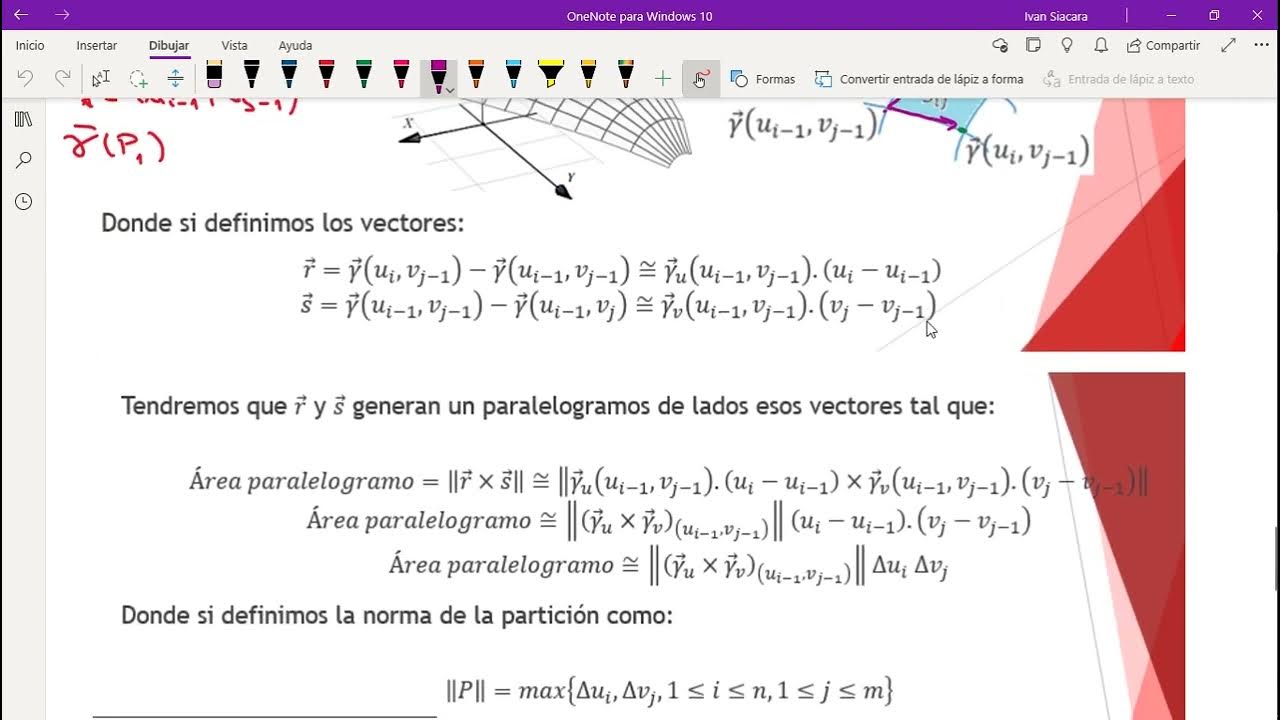
• 🎯 El producto vectorial fundamental es esencial para calcular el área de una superficie parametrizada, y es el producto cruz entre las derivadas parciales de la función vectorial de parametrización.
• 🧮 El área de una superficie suave a trozos se calcula como una doble integral sobre el dominio de parametrización, multiplicado por la norma del producto vectorial fundamental.
• 📏 El cambio de variable y la elección adecuada de la parametrización pueden simplificar significativamente el cálculo del área de una superficie.
• 🔍 El área de una superficie no depende de la parametrización utilizada, siempre y cuando esta sea suave y biyectiva.
• 🌐 Una esfera puede ser parametrizada de diferentes maneras, como por ejemplo, usando coordenadas esféricas o considerándola como una superficie de revolución.
• 📉 El determinante de la matriz formada por las derivadas parciales de la función vectorial de parametrización es crucial para el cálculo del producto vectorial fundamental.
• 🧬 La normalización del producto vectorial fundamental proporciona el vector normal unitario a la superficie en cada punto.
• 🔢 La integral doble sobre el dominio de parametrización del producto vectorial fundamental normalizado permite calcular el área de la superficie.
• 📂 Una parametrización adecuada puede transformar un cálculo complejo en uno más manejable, como se demuestra en el ejemplo del toro autoreferente.
• 🌀 El casquete superior de una esfera, considerado como una superficie de revolución, tiene una parametrización que permite calcular su área de manera más sencilla que la de la esfera completa.

Q & A

¿Qué es un campo escalar y cómo está relacionado con la parametrización de una superficie en r3?

Un campo escalar es una función que asigna un único valor escalar a cada punto de su dominio, que generalmente es un subconjunto de r2 o r3. En el contexto de la parametrización de una superficie en r3, las coordenadas de la superficie son campos escalares en r2, y su derivada parcial existe y son continuas en el dominio de la parametrización.

¿Cómo se define el producto vectorial fundamental en el contexto de una superficie parametrizada?

El producto vectorial fundamental se define como el producto cruz de la derivada parcial de la función vectorial de parametrización con respecto a cada una de las coordenadas del dominio. Este producto vectorial es un vector normal a la superficie en el punto dado y su规范（norma） representa el área del paralelogramo generado por estas derivadas parciales.

¿Por qué el producto vectorial fundamental es ortogonal a las dos derivadas parciales que lo componen?

El producto vectorial de dos vectores en r3 tiene la propiedad de ser ortogonal tanto al primer vector como al segundo. Esto se debe a que el producto vectorial (también conocido como producto de cruz) entre dos vectores produce un tercer vector que es perpendicular a ambos vectores originales.

¿Cómo se determina si una superficie es suave en el punto dado por una parametrización?

Una superficie es suave en un punto dado por una parametrización si el producto vectorial fundamental no es el elemento neutro en el reposador (es decir, no es el vector nulo). Esto indica que las derivadas parciales no son colineales y, por lo tanto, definen una superficie curva en lugar de una superficie plana.

¿Cómo se calcula el área de una superficie parametrizada compuesta por varios trozos?

Para una superficie compuesta por varios trozos, se calcula el área de cada superficie de trozos individualmente y luego se suman las áreas. Cada superficie de trozos debe ser suave y parametrizada por una función vectorial inyectiva.

¿Cómo se calcula el área de una superficie parametrizada?

El área de una superficie parametrizada se calcula como una doble integral sobre el dominio de parametrización de la norma del producto vectorial fundamental. Esto significa integrar el área del paralelogramo generado por las derivadas parciales de la función vectorial de parametrización.

¿Cómo se determina el área de una esfera usando una parametrización?

Para determinar el área de una esfera, se calculan las derivadas parciales de la función vectorial de parametrización con respecto a las coordenadas del dominio. Luego, se calcula el producto vectorial fundamental y su norma, que representa el área del paralelogramo generado por estas derivadas. Finalmente, se integra esta norma sobre el dominio de parametrización.

¿Por qué la elección de la parametrización afecta la facilidad de cálculos para encontrar el área de una superficie?

La elección de la parametrización直接影响到衍生物（derivadas）的形式和复杂性，进而影响到计算产品向量（producto vectorial）和其范数（norma）的难易程度。某些参数化方式可能会简化这些计算，而其他方式可能会使计算变得更加复杂。

¿Cómo se calcula el determinante del producto vectorial fundamental para una parametrización dada?

Para calcular el determinante del producto vectorial fundamental, se forma una matriz cuyas filas son las derivadas parciales de la función vectorial de parametrización y los vectores canónicos en r3. Luego, se calcula el determinante de esta matriz, que equivale al producto vectorial de las derivadas parciales.

¿Cómo se relaciona el área de un paralelogramo con el producto vectorial de los vectores que lo generan?

El área de un paralelogramo generado por dos vectores es igual a la norma del producto vectorial de esos vectores. Esto se debe a que el producto vectorial proporciona una medida de la área del paralelogramo formado por los vectores en el espacio tridimensional.

¿Cuál es la ventaja de utilizar un cambio de variables para calcular el área de una superficie parametrizada?

El cambio de variables puede simplificar la expresión de la función que se está integrando, lo que hace que el cálculo de la integral sea más directo y menos propenso a errores. Además, a veces un cambio de variables puede transformar una integral difícil en una más simple, especialmente si la nueva variable tiene un dominio más natural para la forma de la superficie.

¿Cómo se determina el área de un toro autoreferenciado a partir de su parametrización?

Para determinar el área de un toro autoreferenciado, se calculan las derivadas parciales de su función vectorial de parametrización con respecto a los parámetros. Luego, se calcula el producto vectorial fundamental y se obtiene su norma, que representa el área del paralelogramo generado por las derivadas. Finalmente, se integra esta norma sobre el dominio de parametrización del toro.

Outlines

00:00

😀 Introducción a la parametrización de superficies y el producto vectorial fundamental

Se describe la parametrización de una superficie en R³ utilizando una función vectorial gamma, donde cada coordenada es un campo escalar en R². Se menciona la existencia y continuidad de las derivadas parciales de gamma. El producto vectorial fundamental es definido como el producto cruz de las derivadas parciales de gamma con respecto a sus coordenadas en R², el cual es ortogonal a las derivadas y define un vector normal a la superficie en cada punto. Se destaca la importancia de este producto vectorial para determinar si una superficie es suave y su aplicación para calcular el área de superficies compuestas por varios trozos.

05:00

📐 Cálculo del área de una superficie: doble integral y el producto vectorial fundamental

Se explica el proceso para calcular el área de una superficie suave, que puede ser a trozos, parametrizada por una función vectorial. El área se calcula como una doble integral sobre el dominio de parametrización omega de la norma del producto vectorial fundamental. Se ilustra con un ejemplo práctico: la esfera, parametrizada por funciones trigonométricas en función de sus coordenadas esféricas. Seguidamente, se calculan las derivadas parciales de gamma con respecto a las coordenadas de parametrización y se utiliza el determinante para encontrar el producto vectorial fundamental. Finalmente, se calcula la norma de este producto para integrar y encontrar el área de la superficie.

10:01

🌐 Cálculo del área de una esfera utilizando diferentes parametrizaciones

Se comparan dos parametrizaciones diferentes para la esfera y se muestra que el área de la superficie no depende de la parametrización utilizada. La primera parametrización es en términos de seno y coseno de las coordenadas esféricas, y la segunda lo es como una superficie de revolución. Se calculan las derivadas parciales de gamma para ambas parametrizaciones y se utiliza el producto vectorial fundamental para encontrar el vector normal y su norma. A partir de aquí, se resuelve la integral doble sobre el dominio omega para encontrar el área de la superficie en cada caso, mostrando que ambos métodos dan el mismo resultado.

15:02

🤔 Elección de la parametrización para facilitar el cálculo del área de superficies

Se discute la importancia de la elección adecuada de una parametrización para simplificar los cálculos de áreas de superficies. Se utiliza como ejemplo el cálculo del área del casquete superior de una esfera, mostrando que la parametrización en términos de una función escalar y su dominio asociado (un disco en este caso) afecta la facilidad del cálculo. Se calculan las derivadas parciales de gamma con respecto a las coordenadas del dominio y se determina el producto vectorial fundamental y su norma. Se resuelve la integral doble sobre el dominio para encontrar el área, y se destaca la complejidad que puede agregar una parametrización menos adecuada.

20:04

🏗 Cálculo del área de un toro auto-esférico a través de su parametrización

Se presenta la parametrización de un toro auto-esférico y seguidamente se calculan las derivadas parciales de gamma con respecto a las coordenadas de parametrización. Se forma el producto vectorial fundamental a partir de estas derivadas y se calcula su norma. Con base en la norma del producto vectorial, se resuelve la integral doble sobre el dominio de parametrización, que es un rectángulo, para encontrar el área de la superficie del toro. Se destaca que la integral de ciertas funciones trigonométricas sobre el dominio es nula,简化了一些计算步骤. Finalmente, se obtiene el área total del toro como el resultado de la integral.

Keywords

💡Superficie

Una superficie en el contexto del video es una extensión tridimensional en el espacio R³ que puede ser parametrizada por funciones vectoriales. Es el objeto principal de estudio para determinar áreas y propiedades geométricas. En el video, la superficie es explorada a través de su parametrización y se utiliza para calcular su área.

💡Función vectorial

Una función vectorial en el video se refiere a una asignación que lleva un punto de un dominio en R² a un vector en R³. Se utiliza para parametrizar superficies en el espacio tridimensional, y es fundamental para definir el producto vectorial fundamental y calcular áreas de superficies.

💡Producto vectorial fundamental

El producto vectorial fundamental, también conocido como el tensor de métrica o el vector normal a la superficie, es el producto vectorial (cruz) entre las derivadas parciales de la función vectorial parametrizando la superficie. Su norma proporciona una medida de la longitud del vector normal y es utilizada para calcular el área de la superficie.

💡Derivada parcial

Las derivadas parciales son funciones que mediran la tasa de cambio de una función vectorial con respecto a una de sus variables, manteniendo las demás constantes. En el video, las derivadas parciales de la función vectorial con respecto a los parámetros de parametrización son esenciales para construir el producto vectorial fundamental.

💡Campo escalar

Un campo escalar es una asignación de un número escalar a cada punto de un dominio en el espacio. En el video, se menciona el uso de campos escalares para definir la parametrización de superficies, como en el caso de la superficie de una esfera o un casquete de esfera.

💡Área de superficie

El cálculo del área de una superficie es una de las actividades principales del video. Se realiza a través de la integración doble del producto vectorial fundamental sobre el dominio de parametrización. El área de superficie es un concepto crucial en geometría diferencial y tiene aplicaciones en física y diseño de estructuras.

💡Parametrización de una superficie

La parametrización es el proceso de representar una superficie mediante una función vectorial que mapea un dominio en R² a puntos en R³. Es una técnica utilizada para simplificar el estudio de propiedades de la superficie, como se muestra en el video al calcular áreas y encontrar vectores tangentes.

💡Vector normal

Un vector normal a una superficie en un punto dado es un vector que es perpendicular a la superficie en ese punto. En el video, el producto vectorial fundamental se utiliza para encontrar el vector normal, el cual es esencial para calcular el área de la superficie y entender su geometría local.

💡Integral doble

Las integrales dobles son una generalización de las integrales simples que se utilizan para calcular áreas, volúmenes y otras propiedades en varias dimensiones. En el video, las integrales dobles son el método elegido para calcular el área de superficies parametrizadas.

💡Esfera

La esfera es un objeto geométrico tridimensional perfecto y simétrico, estudiado en el video a través de diferentes parametrizaciones. Se utiliza como ejemplo para ilustrar cómo calcular el área de superficie utilizando el producto vectorial fundamental y las integrales dobles.

💡Toro

Un toro es una superficie tridimensional que se forma retorciendo un círculo en el espacio. En el video, se proporciona una parametrización para un toro y se calcula su área, demostrando cómo las diferentes formas de parametrizar un objeto pueden afectar la facilidad del cálculo.

Highlights

Introducción a la parametrización de superficies en R³ utilizando funciones vectoriales.

Explicación de las propiedades del producto vectorial fundamental y su relevancia en la normalización a una superficie.

Descripción de cómo las derivadas parciales de una parametrización definen vectores tangenciales a una superficie.

Importancia de la existencia y continuidad de las derivadas parciales para la parametrización de una superficie.

Definición del área de una superficie suave a trozos y su relación con el producto vectorial fundamental.

Método para calcular el área de una superficie parametrizada utilizando dobles integrales.

Ejemplo práctico de cálculo del área de una esfera utilizando dos diferentes parametrizaciones.

Demostración de que el área de una superficie no depende de la parametrización utilizada.

Cálculo del área del casquete superior de una esfera como una aplicación de la parametrización de superficies.

Uso de campos escalares para definir la parametrización de una superficie, en este caso, el casquete de una esfera.

Importancia del dominio de parametrización en el cálculo del área de una superficie.

Comparación de la facilidad en el cálculo del área de una superficie de revolución versus una parametrización más complicada.

Ejemplo del cálculo del área de un toro autoreflexivo utilizando parametrización de donut.

Proceso para calcular las derivadas parciales de una parametrización y su impacto en el producto vectorial fundamental.

Cálculo del determinante y la norma del producto vectorial fundamental para una parametrización específica.

Integración sobre el dominio de parametrización para encontrar el área de una superficie dada.

Conclusión sobre la no complejidad relativa del cálculo del área de una superficie parametrizada.

Transcripts

[Música]

[Aplausos]

[Música]

hola chicos veamos ahora área de

superficies sea s una superficie en r3

parametrizar por mi función vectorial

gamma y voy a pensar que cada una de sus

coordenadas es un campo escalar en r2

cuya derivada parcial existe y son

continuas en el abierto de regla

recuerden que cuando digo abierto no

considero en la frontera vale entonces

esas tres campos cada vez están

definidos en la beta omega omega es el

dominio de mi parametrización se define

el producto victoria fundamental como el

producto cruz de la deriva parcial de

gamma con respecto a ere producto cruz

derivada parcial de gamma con respecto a

ese para todo el r&s en el ámbito de

hormiga vale recuerde que la derivada la

derivada de gamma con respecto a ere o

bien con respecto a s son vectores en r3

que quiere decir el producto cruz de dos

vectores en r3

recuerden que una de las propiedades es

que este vector es un vector ortogonal

tanto a en este caso tanto a la deriva

parcial de gamma con respecto a m o bien

y también es ortogonal a la deriva

parcial de granma con respecto a ese es

una de las propiedades del producto cruz

cierto si yo tengo dos vectores en r3 el

producto cruz es un vector ortogonal

tanto al vector al primer vector como el

segundo vector vale bueno

entonces hacemos que el producto

victoria fundamental no va a definir un

vector normal a la superficie

en un punto de reserva es ese no si yo

lo evalúo a mi producto vectorial

fundamental en ese punto aquí tengo mi

dominio mega mi dominio de mí para mi

utilización y aquí tengo mi superficie s

entonces gama de rsr 0 s 0 pues es este

punto de aquí en la derivada de gamma

con respecto a r en el punto 0 s 0 es un

vector un vector tangencial a una curva

una curva sobre mi superficie vale

entonces esta derivada me va a definir

vectores tangenciales esta curva esta

curva que viene por aquí y en este punto

pues es este vector ya no habla y

análogamente si yo dejo fijo

a r digamos en el punto de relleno

entonces la derivada parcial de gamma

con respecto a s en el punto de 0 s me

va a definir una curva ale esta curva

perdón va a ser va a ser un vector

tangencial de esta curva y en este punto

pues está este vector entonces tengo que

las derivadas son vectores tangenciales

a estas curvas que se dicen aquí vale

entonces que me dice el producto como es

una de las propiedades del producto cruz

es un vector normal tanto al primer

vector como al segundo vector y este

vector

normal a la superficie en este punto en

el punto r 0 s 0

como notación si gamma es una

parametrización de una superficie se la

voy a denotar así si simplemente sí

definición una no va a considerar una

superficie parametrizar por gamma yo voy

a decir que esta superficie suave si el

producto vectorial fundamental no es el

elemento neutro en el represor sale

bueno entonces si la superficie s es una

superficie compuesta por varias

superficies digamos s1s2 hasta s acá

vamos a decir que ese es una superficie

trozos y se va a escribir de esta forma

es lo análogo a curvas a trozos y se dan

cuenta una superficie a trozos s 1

compuesta por s1s2 hasta esté acá se

dice que suave a trozos y cada una de

estas superficies es suave sale entonces

éste

para determinar el área de una

superficie vamos a hacer lo siguiente

voy a considerar una superficie suave

puede ser a trozos y parametrizar por

una función vectorial

una función que va de omega es un

subconjunto de r2 a mi superficie tal

que a cada punto de la superficie se le

corresponde un único punto de omega esto

quiere decir que mi función vectoriales

inyectaba entonces el área de la

superficie se puede calcular como una

doble integral sobre omega de la norma

del producto vectorial fundamental aquí

es de r lbs tales están esté escribiendo

pongan aquí de erre por favor y como

notación lo voy a escribir así la doble

interior el sobre se sale diferencial s

mayúscula ok el área de la superficie s

dijimos que está dado por la doble

integral de omega de la norma del

producto vectorial fundamental que

significa la norma de un producto cruz

de dos vectores en r3

si recuerdan de su curso de álgebra

lineal la norma de un producto cruz de

dos vectores mr3 me determina un área

del paralelogramo generado por estos dos

vectores vale a veces y sí me considero

si yo tomo un cuadriculado del dominio

de mi parametrización y me tomo un punto

sobre uno de sus vértices y lo mapeo

para dar un punto sobre la superficie la

derivada de gamma con respecto a herriko

respecto de si me va a dar me van a dar

dos vectores dos vectores tangencial

esas dos curvas como ya lo vimos

anteriormente sale entonces si yo

multiplico por ejemplo a delta r por la

derivada parcial de gamma con respecto a

rpp va a dar un vector muy pequeño y si

yo multiplico a directa s por la

derivada parcial de gamma con respecto a

eso me va a dar otro vector pequeño

entonces es el área de este cuadrado

pues va a ser aproximadamente igual a la

norma del producto

del producto cruz de los vectores delta

r derivada parcial de gamma con respecto

a r

delta ese derivado parcial de gamma con

respecto a s

van a ser muy parecidos y el área del

paralelogramo va a ser aproximadamente

igual al al cuadrado que se proyecta

sobre la superficie se si se fijan aquí

abajo son aproximadamente iguales es

como si estuvieran poniendo los tics en

mi superficie y el área de estos post yx

que son las áreas de mis paralelo gramos

son aproximadamente igual al área que

proyecta sobre mi superficie si el delta

ese y el delta r pueden salir del prode

el del producto cruz por una de las

propiedades y salen también con

propiedades de la norma aquí sería del

traer del tc entonces aquí tendré yo dos

sumas ok

porque estoy sumando todos los

rectángulos que están aquí que los

multiplicó de esta forma para obtener

estos rectángulos que están desde sobre

los mismos tics de mi superficie

entonces al tomar el límite lo que

estamos haciendo entonces está bien

justificada esta fórmula le damos un

ejemplo

a ver

vamos a determinar el área de esta

superficie una esfera se entra en el

origen de radio r entonces sabemos que

una para mi superficie está por el seno

de r chiquita con seno de ese ere se

modere chiquita seno de ese ere coseno

de chiquita donde r va de cero y ese va

a desear a dos pi en la primera

parametrización de la escena que vimos

entonces para determinar el área de la

superficie hay que calcular la derivada

parcial de gamma con respecto a r y la

derivada de gamma con respecto a ese

entonces vamos a derivar primera llama

con respecto a r la derivada seno es

coseno entonces tengo r coseno de

ritchie kitoko seno de s vamos a derivar

otra vez aquí y me queda r coseno drs no

desde chiquita y menos ere seno de

chiquita ahora vamos a derivar haga más

con respecto a ese entonces la deriva de

coseno - seno no me queda menos r seno

de r chiquita seno de ese ere seno de

chiquita coseno de s en la derivada y

aquí como no depende de ese es cero

que necesitamos hacer ahora es calcular

el producto vectorial fundamental que es

calcular el producto cruz de estos dos

vectores en el retraso entonces a

calcular el determinante de esta matriz

si recuerdan primera fila y jk mis

vectores canónicos en r3 mi segunda fila

es la derivada parcial de gamma con

respecto a r sobre los elementos y la

tercera fila son los elementos de la

derivada de gamma con respecto a es anne

quiero que pongan pausa al vídeo y que

me calculen este determinante

quiero que verifiquen que el

determinante de esta matriz que viene

dada por este vector ale r cuadrada seno

cuadrado de chiquita coseno de ese ere

cuadrada seno cuadrado de chiquitas en

ourense y erre cuadrada coseno de reig y

quita seno de requisitos entonces que

nos falta hacer calcular su normal la

normal de este vector entonces es raíz

cuadrada de la primera coordenada al

cuadrado mala segunda coordenada al

cuadrado más la tercera coordenada al

cuadrado

entonces se fijan en las primeras dos

puedo factorizar era la cuarta seno

cuadrado de r álex seno cuadrado

de hecho hacemos la cuarta y tendré yo

por coseno cuadrado de s más se nos

cuadra 2 x 1 entonces queda era la

cuarta será la cuarta de r más era la

cuarta coseno cuadrado drs no cuadran

der y factor hizo era la cuarta seno

cuadrado de er y aquí me quedaría un

seno cuadrado de r más coseno cuadrado

de requesón y me queda

cada vez es r cuadrado valor absoluto de

ese poder pero dijimos que rebane

therapies entonces toma un valor mayor o

igual a cero y simplemente se modera y

vamos a integrar sobre omega ere

cuadrado seno del el área de esta

superficie es entonces la integral de

recuadrado seno cuadrado de ere sobre

omega omega es un rectángulo entonces

furini va a ser la integral de cerati

con respecto a r la integral de será los

picos respecto a ese de mi función como

no depende de ese entonces la integral

vale 2 p me queda 2 pr cuadrada por la

integral de será pide seno de rr y la

integral del seno de eres menos coseno

ver evaluó de 0 aquí y me da 24

calculemos ahora el área de la misma

superficie de mi esfera se entra en el

origen de radio r considerando otra

parametrización y veamos que no depende

el área de la superficie no depende de

la parametrización entonces ya vimos que

s con más raíz cuadrada de re cuadrado

al menos s cuadrada coseno de r con más

raíz cuadrada de re cuadrada menos s

cuadrada seno de r donde r vale 02 pig y

s d - r r de menos r

también es una parametrización de mi

esfera si estoy esta parametrización es

si yo pienso a mi esfera como una

superficie de revolución

bueno pues para calcular el área

necesitamos calcular la derivada parcial

de gamma con respecto a r y calcular la

derivada parcial de gamma con respecto a

s la derivada de gamma con respecto a r

pues primera coordenada no depende de r

pues en 0 sale la segunda es derivar

coseno con respecto a r que es es es

menos e no los tengo menos raíz cuadrada

de re cuadrada menos s cuadrado seno de

r aquí está y acá tendría raíz cuadrada

de cuadrada menos está encuadrada

derivada de seno cocer haré ahora con

respecto a ese primera coordenada es 1

derivó coseno y seno son funciones

constantes entonces sería 1 entre dos

veces la raíz cuadrada de re cuadrado

menos ese cuadrado

la derivada de lo que está dentro de la

raíz que es menos 2 s los dos se van y

me queda simplemente menos s por coseno

de r sobre la raíz cuadrada y en la

tercera coordenada queda alguna luego me

queda menos s porsche no tiene función

constante sobre la raíz cuadrada

entonces ahora hay que dar que hay que

hacer es calcular el producto vectorial

fundamental el producto cruz de los dos

de las derivadas de los vectores

anteriores

más bien el producto cruz de la deriva

parcial de gamma con respecto a r y de

la derivada parcial de gamma con

respecto a esa primera fila es el

determinante de esta matriz primera fila

los canónicos en r3 segunda fila los dos

las coordenadas de la derivada de gamma

con respecto a las coordenadas de la

deriva de gamma con respecto a ese en la

tercera fila quiero que pongan pausa el

vídeo y que me calculen el determinante

de esta matriz

quiero que verifiquen que eléctrica del

vector s como a raíz cuadrada de re

cuadrada menos s cuadrada coseno de r

coma raíz cuadrada de re cuadrada menos

s cuadradas seno de r shane vamos a

calcular la norma que es raíz cuadrada

de la primera coordenada al cuadrado más

la segunda coordenada al cuadrado más la

tercera coordenada al cuadrado puedo

factorizar aquí es cuadrada menos s

cuadrada me queda coseno cuadrado más

seno con lo que es 1 y r cuadrada menos

seno cuadrado más perdón ere cuadrada

menos s cuadrada más ese cuadrado que me

queda de re cuadrada raíz cuadrada de re

cuadrada

r vale entonces el área de la superficie

en la doble integral sobre omega omega

es un rectángulo de r y esto es el revés

es el área donde ella es un rectángulo

2 pib por 12 r 4 pies cuadrada entonces

si yo considero esta parametrización es

la parametrización anterior pensando a

mi esfera como una superficie de

revolución me se me hace más fácil

determinar leer el área de la superficie

y cierto es simplemente calcular la

doble integral de r sobre media que su

rectángulo organismo más fácil bueno

vamos ahora a considerar otra

parametrización pero ahora voy a pensar

que vaya a calcular el área del casquete

superior de la esfera y al final lo voy

a multiplicar por 2 porque va a ser la

misma área que el casquete inferior de

la de la esfera porque voy a

parametrizar la parte superior para

pensar que el casquete superior proviene

de la gráfica de un campo es canal n

entonces como viene dada la una

parametrización pensándolo así a mi

superficie como rs como frs mi campo me

[Música]

el campo escalar en r2 va a ser raíz

cuadrada es despejar se está aquí más

bien y tomar el signo positivo y donde

una equis pongo r y donde veo nadie

pongo ese sale y obtengo este de aquí

ahora el dominio de gamma va a ser el

dominio de mi campo escalar que va a ser

la sombra de mickey de mi casquete

superior de la esfera que va a dar un

disco aquí esta conjunto de parejas

ordenadas x jetta leds que x cuadrada

más de cuadrada es menor o igual que

recuerdo entonces tengo que mi dominio

de mi gama ya no es un rectángulo sino

un disco

pero vamos a calcular la derivada

parcial de gamma con respecto a r que

sería 10 y aquí tendría 1 entre dos

veces la raíz cuadrada de re cuadrada

menos recordada chiquita menos s

cuadrada por la derivada con respecto a

r del argumento de la raíz que sería

menos 2 r los dos se van y me queda

simplemente estoy aquí y con respecto a

ese pues es 0 1 y lo análogo nada más

que ahora va a ser aquí menos s vale

ahora vamos al calcular el producto de

victoria fundamental

el determinante de esta matriz y

verifique que les tiene que dar r sobre

raíz cuadrada de re cuadrada - r

cuadrada menos s cuadrada con mã s /

raíz cuadrada de re cuadrada menos erre

cuadrada menos ese cuadrado como ahora

ahora vamos a calcular la norma y que

sería raíz cuadrada

del primera coordenada al cuadrado más

la segunda coordenada al cuadrado más 1

pues aquí les quedara encuadrada tienen

el mismo este denominador voy a hacer un

denominador al cuadrado es cierto no

sería r cuadrada más s cuadraba entre

ere cuadrada - r cuadrada menos s cuadra

diciendo sumar este ere cuadradas iría

con el ere cuadrada ls cuadras e iría

con el s cuadrada y simplemente les

quedaría ere cuadrada sobre sobre ere

cuadrada - r cuadrada menos s cuadrada y

la raíz pues ese ere sobre la raíz de

ere cuadrada - r cuadrada menos s

cuadrado vale quiero que pongan pausa el

vídeo y que hagan ustedes las cuentitas

salen las normales tiene que dar esto de

aquí entonces veces la doble integral

sobre omega sobre mi disco que la

función que queda aquí sale pero que

creo es cómo es mi dominio es un disco

puedo hacer cambio de variable ok

voy a poner a er como p coseno de teta y

a s como p seno de teta

recuerden que tengo que pagar con mi

gobierno que sería de saleh y aquí éste

puede factorizar cuadrada y tendría seno

cuadrado más coseno cuadrado que es uno

y les quedan simplemente el p cuadrado

ok entonces les queda cómodo se arregla

integral de ser r con respecto a p la

integral de 0 2 p

con respecto a teta de mi función p /

raíz cuadrada de re cuadrada - p

cuadrada en de detecta sangre

entonces me queda 2 x 12 r 4 pierce

integral de será r de mi función con

respecto a p hago un cambio de variable

sale me hace falta un menos 1 - 2 p

y la integral de recuadrado de 1 / raíz

cuadrada de recordar - p cuadrada de

raíz cuadrada de re cuadrada menos p

cuadrada por 2 sale y vuelve a obtener

en menos 4 acá está le hago la

evaluación y me da 4 p r cuadrada vale

entonces si yo utilizo esta

parametrización se dificulta bastante

calcular el área de mi superficie sale

chicos hay que tener en cuenta que

parametrización es que utiliza para que

se le faciliten los cálculos bueno

por último ejemplo vamos a determinar el

área de un toro autor es una dona vale

se puede probar que una parametrización

de una dona de un toro es de esta forma

paréntesis

r más coseno de r todo eso por coseno

abc r más coseno de r todo eso por seno

de ese la ley y que sea coordenadas seno

de dónde r&s ambos van de 0 a 2

vale aquí está así es cómo de parametría

por ende será dos parámetros así y

parametrizar así transversalmente ok

bueno entonces que hay que hacer primero

calcular la deriva fácil de gama con

respecto a ere y luego calcular la

deriva parcial de gama con respecto a s

con respecto a r

r coseno de ese es constante la derivada

a vale cero simplemente hay que llevar

coseno de r por coseno desee y es

simplemente de barco se modere me queda

menos seno de r coseno de s menos seno

de r seno de ese y la derivada escena

coseno de a vale aquí que de derivar con

respecto a ese entonces era más coseno

de res constante y derivados con seno de

ese y me queda menos

r más coseno de r todo eso por x seno de

ese lenguaje

r más coseno de ere por la derivada de

seno que escogemos la tercera coordenada

no depende de ese entonces vale ser

ahora hay que calcular el producto

victoria fundamental entonces quiero que

pongan pausa el vídeo y que ver y que

calculen el determinante de esta matriz

y que les tiene que dar igual este

electrón acá sale entonces la norma va a

ser raíz cuadrada de la primera

coordenada al cuadrado más la segunda

coordenada al cuadrado

más la tercera coordenada al cuadrado

aquí si se fijan puedo factorizar ere

más coseno de r

al cuadrado por coseno cuadrado de n y

les va a quedar coseno cuadrado de ese

más seno cuadrado de sx1 no les queda

más coseno de r todo es al cuadrado

coseno cuadrado de r de estos dos mangas

r más coseno de entonces al cuadrado por

seno cuadrado del factor y sam oeur

mascó se modera al cuadrado tienen que

ser un cuadrado de r seno cuadrados de

ricky es uno y les queda

r más coseno cuadrado de real cuadrado

raíz cuadrada pues es r más costero de

el saler

tanto el área de un toro he estado por

nado por la integral de er más coseno de

r sobre mira donde un mes es un

rectángulo entonces propiedad de la

integral que sería la integral de ere

sobre omega

pero eres una costa entiendo sería tres

veces el área donde la más joven y sería

la integran de cerrado speech con

respecto a ese aquí va un diferencial

ese integral de cero dos picos seno de r

pero la integral de cerramos pico seno

de r con respecto de rezar o toda esta

parte vale cero simplemente me queda el

revés cenar ya la vega sale omega es el

producto cartesiano de los intervalos

cerrados

02.02 pi que es 4 pi cuadrada sale

entonces sería el área es 4 pi cuadrada

poner aves chicos no está tan complicado