Volumen de un Sólido de Revolución usando Discos
Summary
TLDREn esta clase, se explica cómo calcular el volumen de un sólido de revolución usando la técnica de discos con integrales. Se inicia revisando el volumen de un prisma y un cilindro para luego abordar el cálculo de sólidos generados al rotar funciones en torno a un eje, como el cilindro generado por la función f(x) = 2. A través de ejemplos visuales, se muestra cómo usar el software GeoGebra para graficar y calcular estos volúmenes, concluyendo con el cálculo del volumen del sólido generado por la función f(x) = √x al rotar alrededor del eje x.
Takeaways
- 🧑🏫 El video enseña cómo calcular el volumen de un sólido de revolución utilizando la técnica de los discos con integrales.
- 🔢 Se recuerda que el volumen de un prisma es el producto del área de su base por su altura.
- 🔵 Para un cilindro, el volumen se calcula como el área de la base (π por radio al cuadrado) multiplicada por su altura.
- 📈 La función f(x) = 2, acotada entre 0 y 6, al rotar alrededor del eje x, genera un cilindro.
- 🔄 Un sólido de revolución se genera al girar una curva alrededor del eje x, en este caso f(x) = √x.
- 📐 El volumen de un sólido de revolución se encuentra sumando el volumen de discos infinitesimales mediante una integral.
- ⚙️ La integral utilizada para encontrar el volumen del sólido es ∫[0,9] π(x) dx, lo que resulta en 127.23 unidades cúbicas.
- 🧮 El proceso se puede resolver gráficamente y numéricamente usando Geogebra y una calculadora científica.
- 📊 En Geogebra, la función se rotó en torno al eje x para generar el sólido de revolución, y se calculó su volumen.
- 👨💻 El resultado final fue de 127.23 unidades cúbicas, tras evaluar la integral y verificar el resultado con herramientas gráficas.
Q & A
¿Qué es un prisma y cómo se calcula su volumen?
-Un prisma es una figura tridimensional que se forma elevando una cara, generalmente un polígono, a una altura constante. El volumen de un prisma se calcula multiplicando el área de su base por su altura.
¿Cómo se calcula el volumen de un cilindro?
-El volumen de un cilindro se calcula multiplicando el área de su base (un círculo) por su altura. El área de la base es \( \pi r^2 \), donde \( r \) es el radio del círculo.
¿Qué es un sólido de revolución?
-Un sólido de revolución es una figura tridimensional que se genera al rotar una curva alrededor de un eje. En el ejemplo del video, la curva se rota alrededor del eje x para formar un cilindro o un sólido similar.
¿Cómo se genera un cilindro mediante la rotación de una función constante?
-En el video, se genera un cilindro al rotar la función constante \( f(x) = 2 \) en el intervalo [0,6] alrededor del eje x. Al girar esta recta, se forma un cilindro con radio 2 y altura 6.
¿Qué es la técnica de los discos en el cálculo de volúmenes?
-La técnica de los discos es un método utilizado para calcular el volumen de un sólido de revolución. Se corta el sólido en discos pequeños de grosor diferencial \( dx \), se calcula el volumen de cada disco y luego se integra para obtener el volumen total.
¿Cómo se calcula el volumen de un sólido generado al rotar \( f(x) = \sqrt{x} \) alrededor del eje x?
-Se utiliza la técnica de los discos para calcular el volumen. El volumen de cada disco es \( \pi (f(x))^2 dx \), y al integrar esta expresión entre 0 y 9 se obtiene el volumen total del sólido, que es 127.23 unidades cúbicas.
¿Cómo se simplifica la integral para encontrar el volumen del sólido?
-La integral que representa el volumen se simplifica usando que \( f(x) = \sqrt{x} \), por lo que \( (\sqrt{x})^2 = x \). La integral se resuelve como \( \int_0^9 x dx = \frac{x^2}{2} \), evaluada entre 0 y 9, lo que da \( 81\pi/2 \), que es aproximadamente 127.23.
¿Qué herramienta se utiliza en el video para graficar y visualizar el sólido de revolución?
-Se utiliza la aplicación Geogebra para graficar la función \( f(x) = \sqrt{x} \) y generar el sólido de revolución en un espacio tridimensional.
¿Qué función se utiliza en Geogebra para generar el sólido de revolución?
-En Geogebra, se utiliza la función 'superficie de rotación' para girar la función \( f(x) = \sqrt{x} \) alrededor del eje x y generar el sólido de revolución.
¿Cómo se calcula el volumen de un sólido de revolución en Geogebra?
-En Geogebra, se utiliza la función 'integral' para calcular el volumen del sólido, ingresando la expresión de la integral definida de \( f(x) = \sqrt{x} \) entre los límites de 0 a 9. El resultado es 127.23 unidades cúbicas.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Integrales triples 1
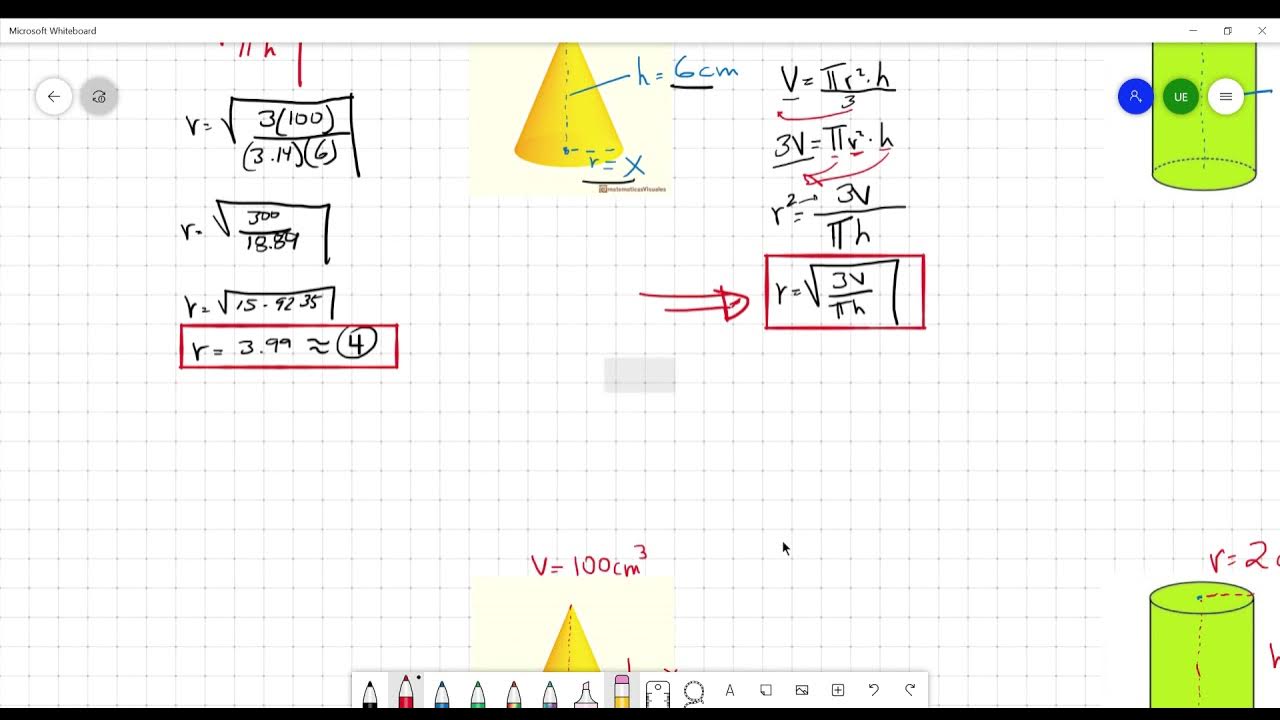
Altura y Radio de un Cilindro y Cono Considerando el Volumen (Solidos en Revolución).

02 Función de distribución normal

08-3) Integral de área HB
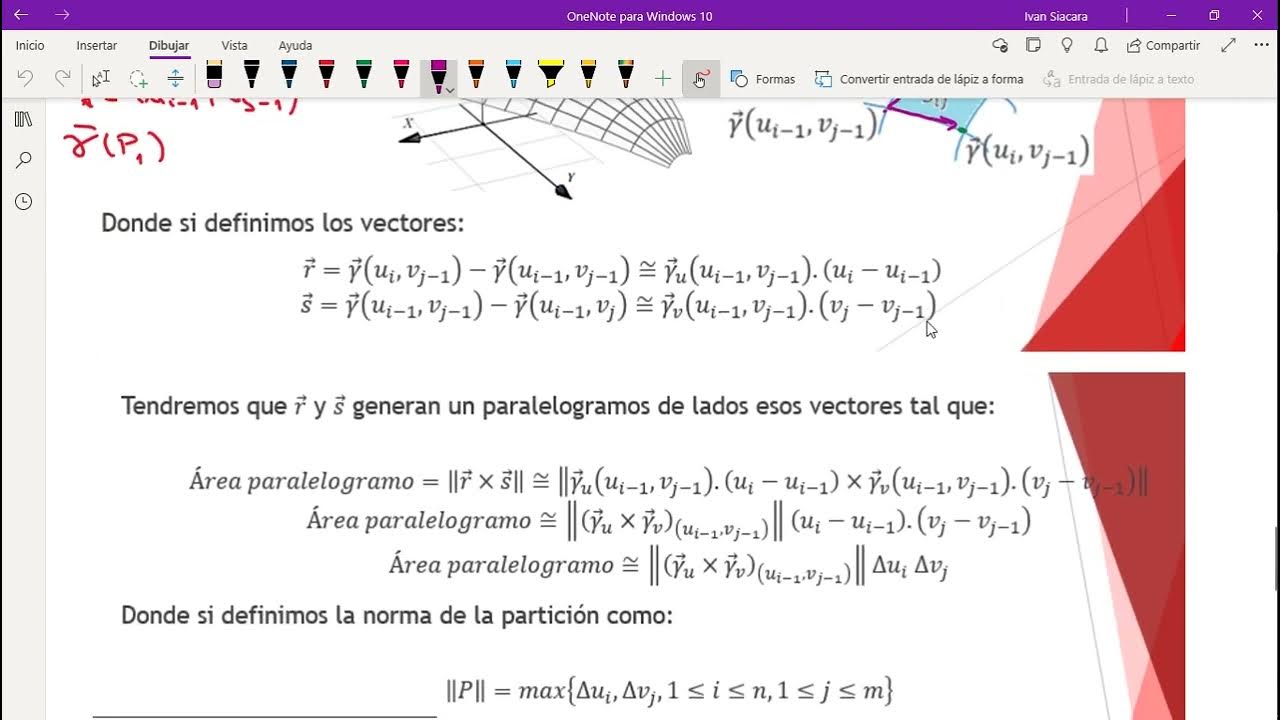
Clase 16 (2da Parte): Integrales de Superficie (campos escalares)

Volumen entre 2 cilindros verticales y logaritmo natural | POLARES | Ej. 36 Sección 14.3 LARSON
5.0 / 5 (0 votes)
