PROBLEM SOLVING WITH PATTERNS || MATHEMATICS IN THE MODERN WORLD
Summary
TLDRThis video discusses problem-solving techniques using patterns and sequences, focusing on concepts like difference tables and Fibonacci numbers. It explains how to predict the next term in a sequence by analyzing differences and how to find the general nth term formula for arithmetic sequences. The video also covers the Fibonacci sequence, its properties, and methods for calculating specific terms using Binet’s formula. With practical examples and step-by-step demonstrations, the video helps viewers understand sequence patterns and apply mathematical formulas to solve problems.
Takeaways
- 📐 A sequence is an ordered list of numbers where each number is called a term, denoted as a_n for the nth term.
- 🔢 To find the next term in a sequence, the difference table method can be used by calculating first and second differences.
- 📈 If second differences are equal, it indicates a pattern that can be used to predict the next term in the sequence.
- 📋 The formula for the nth term of a sequence can be derived from patterns, such as a_n = n^2 + n.
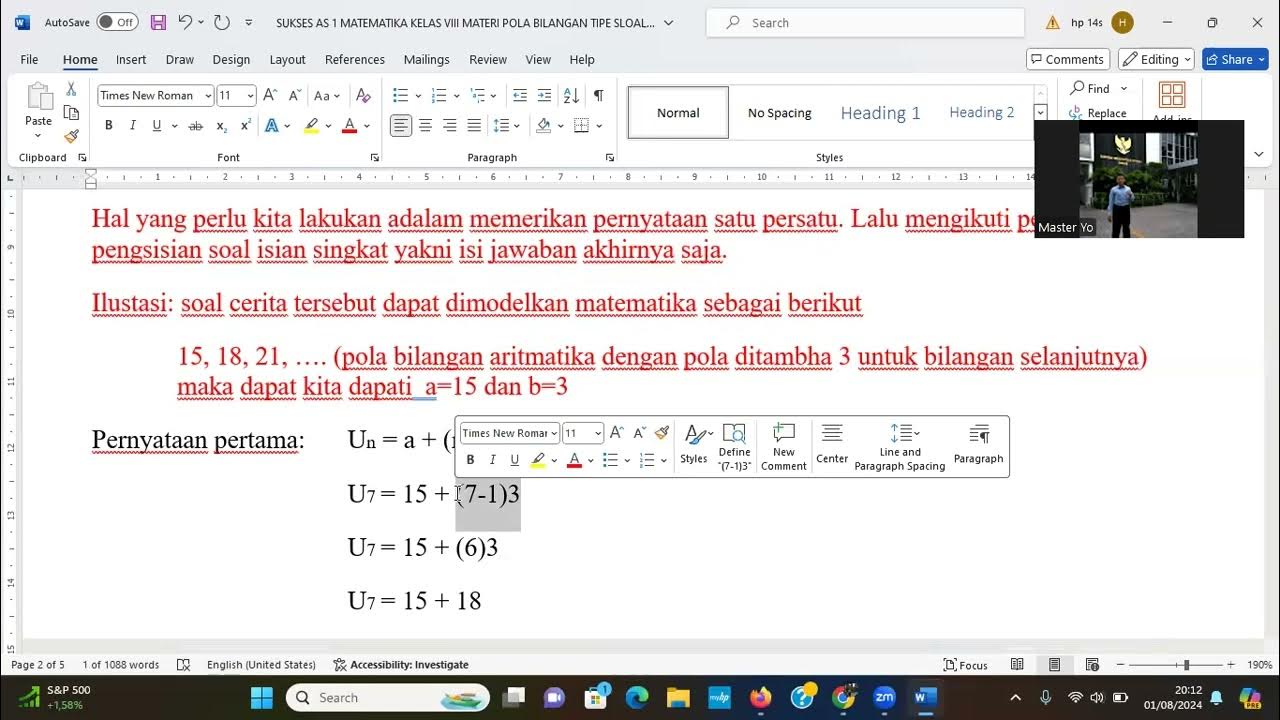
- 🔑 Arithmetic sequences have a common difference, denoted as 'd', which can be used to find any term using the formula a_n = a_1 + (n-1) × d.
- 🧩 The pattern of square tiles can be used to determine the nth term formula, such as a_n = 3n - 1 for a specific pattern of tiles.
- 🌐 The Fibonacci sequence is a series where each number is the sum of the two preceding ones, represented by the formula f_n = f_{n-1} + f_{n-2}.
- 📉 Binet's formula is a direct way to calculate Fibonacci numbers without using a sequence table, involving the golden ratio.
- 🔄 A property of Fibonacci numbers is that for n ≥ 3, 3 × f_{n-1} - f_{n-2} = f_{n+1}.
- ❌ The statement that if n is even, then f_n is even, is false because the pattern of even and odd Fibonacci numbers alternates.
Q & A
What is a sequence in mathematics?
-A sequence is an ordered list of numbers, where each number is called a term. It is a function whose domain is the set of positive integers.
How is the nth term of a sequence denoted?
-The nth term of a sequence is denoted as a sub n (aₙ). For example, a₁ is the first term, a₂ is the second term, and so on.
What method is used in the video to predict the next term of a sequence?
-The difference table method is used to predict the next term of a sequence. By finding the first and second differences, if the differences become equal, the next term can be predicted.
How do you calculate the first differences in a sequence?
-The first differences are calculated by subtracting each term from the next. For example, in the sequence 5, 14, 27, 44, 65, the first differences are calculated as 14 - 5 = 9, 27 - 14 = 13, 44 - 27 = 17, and so on.
How are the second differences calculated, and what does it signify?
-The second differences are calculated by subtracting the first differences from each other. For example, 13 - 9 = 4, 17 - 13 = 4, and so on. If the second differences are equal, it indicates that a pattern can be used to predict the next term.
What is the nth term formula mentioned in the video?
-An nth term formula is a mathematical expression that generates the terms of a sequence. For example, the formula aₙ = 3n² + n can be used to find terms in a quadratic sequence.
How is the common difference used to find the nth term of an arithmetic sequence?
-In an arithmetic sequence, the common difference is used in the formula aₙ = a₁ + (n - 1) × d, where a₁ is the first term and d is the common difference. This formula helps calculate any term in the sequence.
What is the Fibonacci sequence, and how is it generated?
-The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones. The formula to generate the Fibonacci sequence is Fₙ = Fₙ₋₁ + Fₙ₋₂, where Fₙ represents the nth term.
What is Binet’s formula for calculating Fibonacci numbers?
-Binet's formula is a closed-form expression used to calculate Fibonacci numbers directly. It incorporates the golden ratio and is expressed as: Fₙ = (1/√5) × [(1 + √5)/2]^n - [(1 - √5)/2]^n.
How is the difference table method different from Binet's formula when predicting terms in a sequence?
-The difference table method predicts the next term by using differences between terms and relies on identifying a pattern in those differences. Binet’s formula, on the other hand, is a direct mathematical formula used specifically for Fibonacci numbers, which avoids the need to calculate prior terms manually.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Pola bilangan (1) - Mencari suku suatu pola bilangan - Matematika SMP

PT3 KSSM Mathematics Form 2 (Patterns and Sequence) Chapter 1 Complete Revision

Pembahasan BARISAN DAN DERET (Aritmetika & Geometri) KELAS 11 | #MatematikAsik

Pola Bilangan [Part 1] - Mengenal Pola Bilangan
Latihan Soal Pola Bilangan

Curso completo de Raciocínio Lógico para Concursos Públicos 2019 Aula 14
5.0 / 5 (0 votes)