Venn Diagrams

Summary

This lesson focuses on Venn diagrams, a visual method to represent sets and their relationships. It begins with a universal set 'U' shown as a rectangle, and subsets like 'A' are represented by circles within it. Complements of sets are outside the circle but within the rectangle. The lesson also covers intersections (overlapping areas between sets) and unions (combined areas of two sets). Disjoint sets, which do not overlap, are also introduced. Key concepts include how elements belong to one or both sets or none at all, helping visualize set theory.

Takeaways

• 🟥 Venn diagrams visually represent sets and their relationships.
• 🟨 The universal set (U) is depicted as a rectangle in Venn diagrams.
• 🟧 Any subset of U, like set A, is represented by a circle inside the rectangle.
• 🟩 The complement of set A (A prime) includes elements in U but outside of A's circle.
• 🟪 If a set X is a subset of A, its circle is drawn entirely within A's circle.
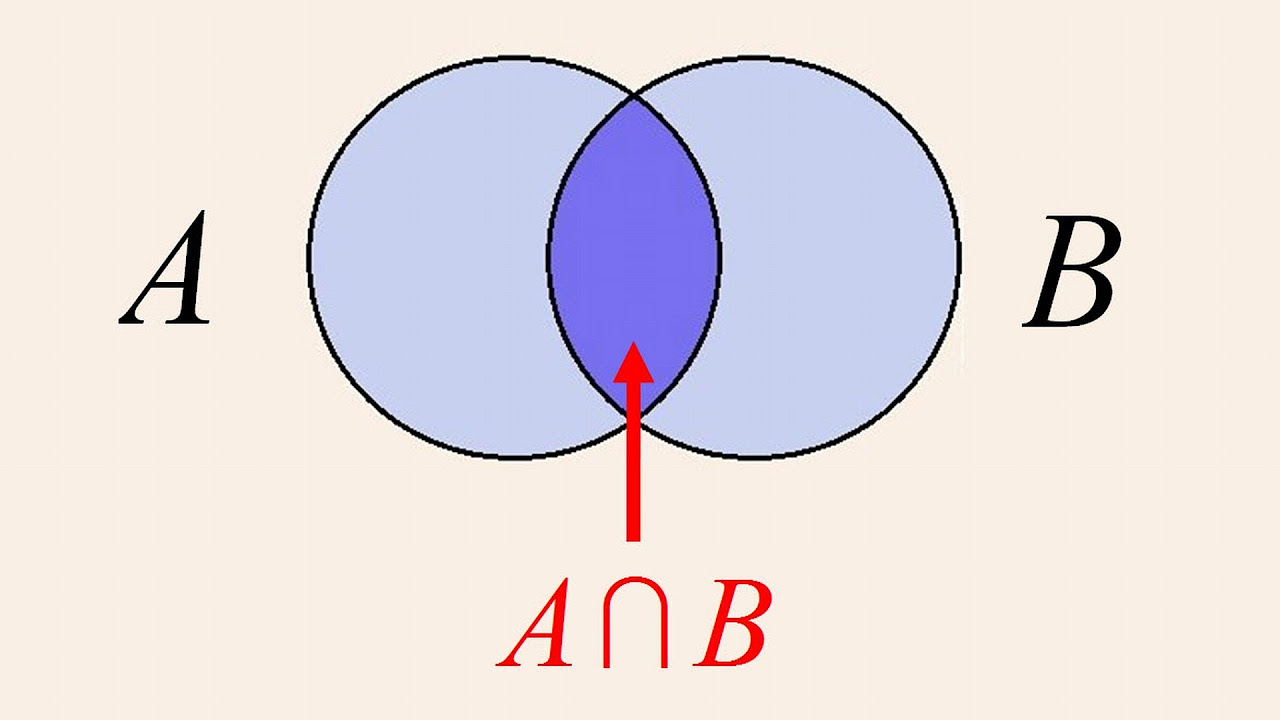
• 🟦 The intersection of two sets (A and B) is the overlapping region, showing elements common to both.
• 🟫 The union of two sets (A and B) is the combined area of both circles, including their overlap.
• 🟨 If two sets do not overlap, they are considered disjoint, meaning no common elements.
• 🟧 Disjoint sets are represented by two non-overlapping circles in a Venn diagram.
• ❓ The lesson concludes by inviting questions and preparing for the next session.

Q & A

What is a universal set in the context of Venn diagrams?

A universal set, denoted as 'U,' is the set that contains all possible elements under consideration in a particular discussion. In a Venn diagram, it is represented by a rectangle.

How are subsets represented in Venn diagrams?

Subsets in Venn diagrams are represented by circles within the rectangle that represents the universal set. Each subset is denoted by a circle, and elements in that circle belong to the subset.

What does the complement of a set refer to?

The complement of a set refers to all elements in the universal set 'U' that are not in the subset. In Venn diagrams, it is represented by the area inside the rectangle but outside the circle of the subset.

How do you represent a subset within another subset in a Venn diagram?

A subset within another subset is represented by drawing a circle (representing the smaller subset) completely inside the circle of the larger subset. This shows that every element of the smaller subset is also part of the larger subset.

What does the intersection of two sets represent?

The intersection of two sets, denoted by 'A ∩ B,' represents the elements that are common to both sets. In a Venn diagram, this is shown by the overlapping region between the two circles representing the sets.

How is the union of two sets represented in a Venn diagram?

The union of two sets, denoted by 'A ∪ B,' includes all elements that are in either set A, set B, or both. In a Venn diagram, the union is represented by the combined area of both circles, including the overlap.

What does it mean for two sets to be disjoint?

Two sets are disjoint if they have no elements in common. In a Venn diagram, this is represented by two circles that do not overlap at all.

What does the overlap of two circles in a Venn diagram signify?

The overlap of two circles in a Venn diagram signifies the intersection of the two sets, meaning the elements that belong to both sets.

If two sets do not overlap in a Venn diagram, what can you conclude about the sets?

If two sets do not overlap in a Venn diagram, they are disjoint, meaning there are no elements that belong to both sets.

How would you visually represent a set's complement in a Venn diagram?

In a Venn diagram, a set's complement is represented by shading the area inside the universal set (rectangle) but outside the circle representing the set. This shows the elements that are not part of the subset.