Riemann approximation introduction | Accumulation and Riemann sums | AP Calculus AB | Khan Academy
Summary
TLDRThis video explains how to approximate the area under the curve of the function y = x² + 1 between x = 1 and x = 3 using four rectangles of equal width. The width of each rectangle is determined, and the height is based on the function's value at the left boundary of each rectangle. Although this method provides an approximation and underestimates the area, the video demonstrates how to calculate the total area. Future videos will explore different approaches for greater accuracy, such as using the right boundary, midpoints, or even trapezoids.
Takeaways
- 🟨 The task is to approximate the area under the curve y = x² + 1 between x = 1 and x = 3.
- 📏 Four rectangles of equal width are used to approximate the area.
- 📐 The width of each rectangle (Δx) is calculated as 1/2, dividing the total interval into four equal parts.
- 📊 The height of each rectangle is determined using the left boundary point of the rectangle, evaluating the function at that point.
- 🧮 Heights for the four rectangles are f(1), f(1.5), f(2), and f(2.5), where f(x) = x² + 1.
- 💡 The approximate area is the sum of the areas of the rectangles, where each area is the product of the height and the base (Δx).
- ➗ The approximate area is calculated as 1/2 × (2 + 3.25 + 5 + 7.25).
- ✅ The total approximate area under the curve is found to be 8.75.
- 🔴 The approximation is an underestimate, as there are portions of the area not covered by the rectangles.
- 🔄 Future videos will cover different methods of approximation, such as using the right boundary, midpoints, or trapezoids.
Q & A
What is the main objective of the video?
-The main objective is to approximate the area under the curve y = x² + 1 between x = 1 and x = 3 using four rectangles of equal width.
How is the width of each rectangle determined?
-The width of each rectangle, delta x, is the total distance traveled in x (from 1 to 3) divided by the number of rectangles (4). This gives delta x = 1/2.
How are the heights of the rectangles defined in this approximation?
-The height of each rectangle is defined by the function evaluated at the left boundary of the rectangle, meaning f(1), f(1.5), f(2), and f(2.5) for the respective rectangles.
Why is this method of approximating the area considered an underestimate?
-This method is an underestimate because some area under the curve is missed in each rectangle, as the rectangles are defined by the left boundary and the curve continues to rise.
How is the total area of the rectangles calculated?
-The total area is the sum of the areas of all four rectangles, each of which is calculated as the height (f(x)) times the width (delta x).
What is the formula used for the approximate area under the curve?
-The approximate area is given by the sum of [f(1) * delta x + f(1.5) * delta x + f(2) * delta x + f(2.5) * delta x].
What are the function values used to calculate the height of each rectangle?
-The function values are f(1) = 2, f(1.5) = 3.25, f(2) = 5, and f(2.5) = 7.25.
How is the final approximate area under the curve calculated?
-After summing the heights and multiplying by delta x, the final approximate area is 8.75.
What could improve the accuracy of this approximation?
-Increasing the number of rectangles would provide a better approximation, as the sum would include smaller sections of missed area.
What other methods for defining the height of rectangles are mentioned?
-Future videos will discuss using the right boundary, the midpoint, and even using trapezoids instead of rectangles to define the height.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

A Tale of Three Functions | Intro to Limits Part I
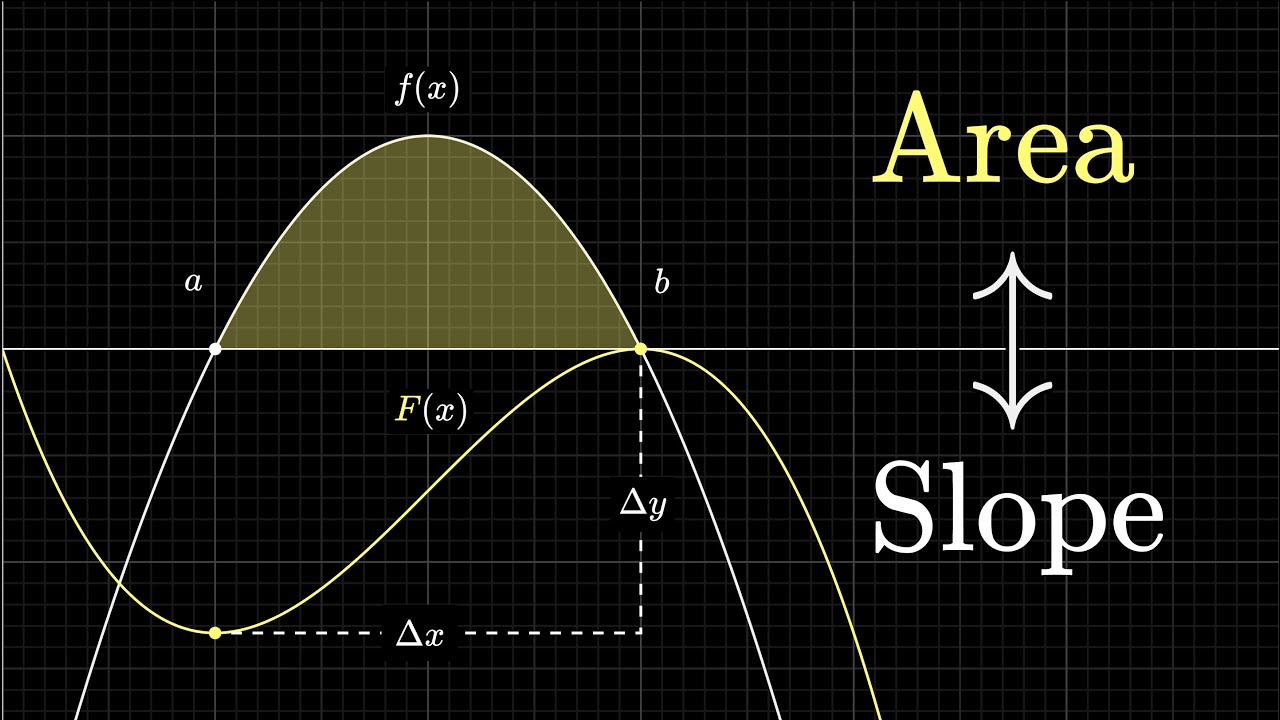
What does area have to do with slope? | Chapter 9, Essence of calculus
Integrales dobles 2
Limit Fungsi Aljabar • Part 1: Konsep Limit Fungsi

Evaluating composite functions | Mathematics III | High School Math | Khan Academy

Average vs Instantaneous Rates of Change
5.0 / 5 (0 votes)