Velocidad promedio y Velocidad instantánea.

Mundo De Mente Académico

4 Feb 202104:07

Summary

TLDREn este vídeo, el canal Mundo Demente explica cómo calcular la velocidad promedio y la velocidad instantánea de una partícula a partir de una gráfica posición vs tiempo. Se calcula la velocidad promedio entre 1.5 y 4 segundos como -2.4 metros/segundo, y la velocidad instantánea a los 2 segundos, usando la pendiente de la recta tangente en ese punto, resulta en -3.7 metros/segundo. El vídeo invita a los espectadores a dejar sus dudas y opiniones en los comentarios.

Takeaways

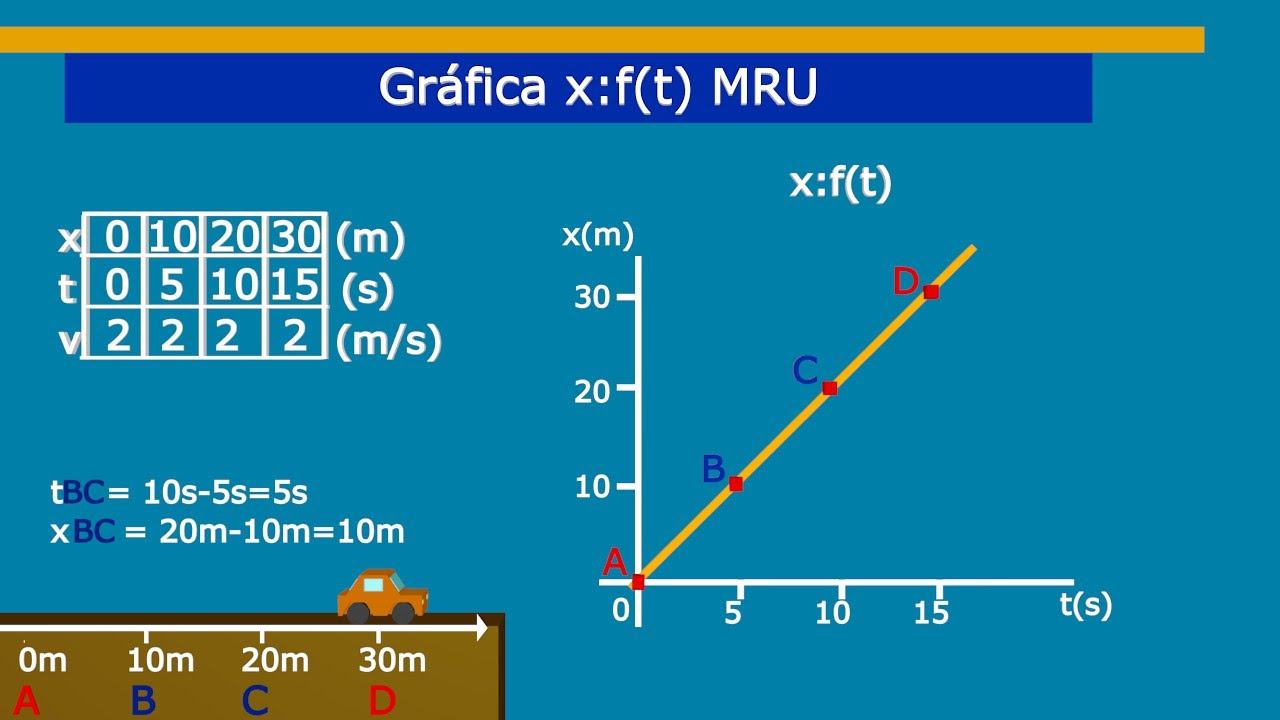
📊 El vídeo explica cómo calcular la velocidad promedio y la velocidad instantánea a partir de una gráfica posición vs tiempo.
⏱️ Se pide calcular la velocidad promedio entre los tiempos de 1.50 segundos y 4 segundos.
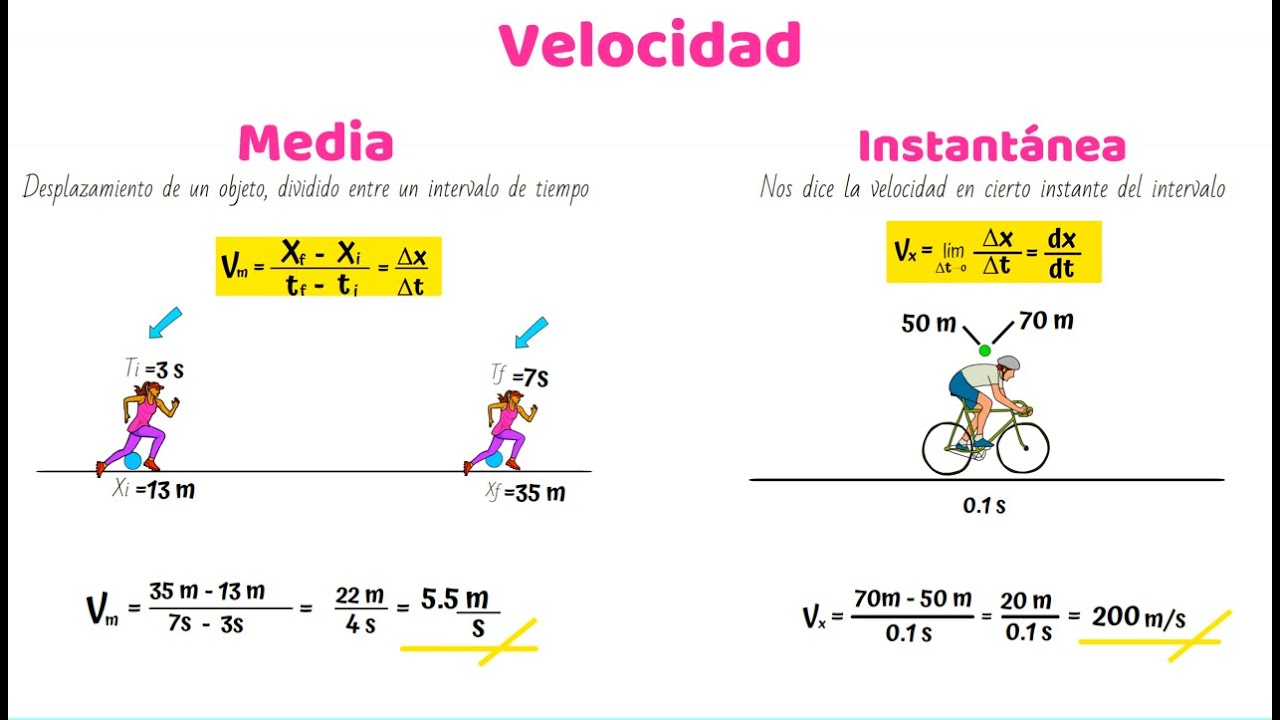
📍 Se menciona que la velocidad promedio se calcula como el cambio en la posición dividido por el cambio en el tiempo.
📉 La posición del tiempo 1.5 segundos es 8 metros y a los 4 segundos es 2 metros.
🔢 La velocidad promedio se calcula como (2 metros - 8 metros) / (4 segundos - 1.5 segundos), dando como resultado -2.4 metros por segundo.
📈 Se pide también determinar la velocidad instantánea a los 2 segundos, que se encuentra en la pendiente de la recta tangente a la gráfica en ese punto.
📌 Se usa la recta tangente que corta el eje del tiempo en 3.5 segundos y el eje de la posición en 0 metros para calcular la velocidad instantánea.
📏 La pendiente de la recta tangente en el punto 2 segundos se calcula como (0 - 13) / (3.5 - 2), dando como resultado -3.7 metros por segundo.
🤔 Se invita a los espectadores a dejar sus dudas y opiniones en los comentarios si tienen alguna pregunta.
🔔 Se recuerda a los espectadores suscribirse al canal y activar la notificación para recibir actualizaciones de nuevos vídeos.

Q & A

¿Qué es la velocidad promedio y cómo se calcula?
-La velocidad promedio es el cambio en la posición dividido por el cambio en el tiempo. Se calcula como la pendiente de la recta que une los puntos de tiempo y posición dados.
¿Cuál es el intervalo de tiempo considerado para calcular la velocidad promedio en el ejercicio?
-El intervalo de tiempo considerado es de 1.50 segundos a 4 segundos.
¿Cómo se determina la posición de la partícula a los 1.5 segundos y a los 4 segundos?
-A los 1.5 segundos, la partícula está en una posición de 8 metros y a los 4 segundos, está en una posición de 2 metros.
¿Cuál es la velocidad promedio entre los 1.5 segundos y los 4 segundos?
-La velocidad promedio es de -2.4 metros por segundo, calculada como (2 metros - 8 metros) / (4 segundos - 1.5 segundos).
¿Qué significa un valor negativo para la velocidad promedio?
-Un valor negativo para la velocidad promedio indica que la partícula está moviendose en dirección opuesta al eje positivo de la posición.
¿Qué es la velocidad instantánea y cómo se determina?
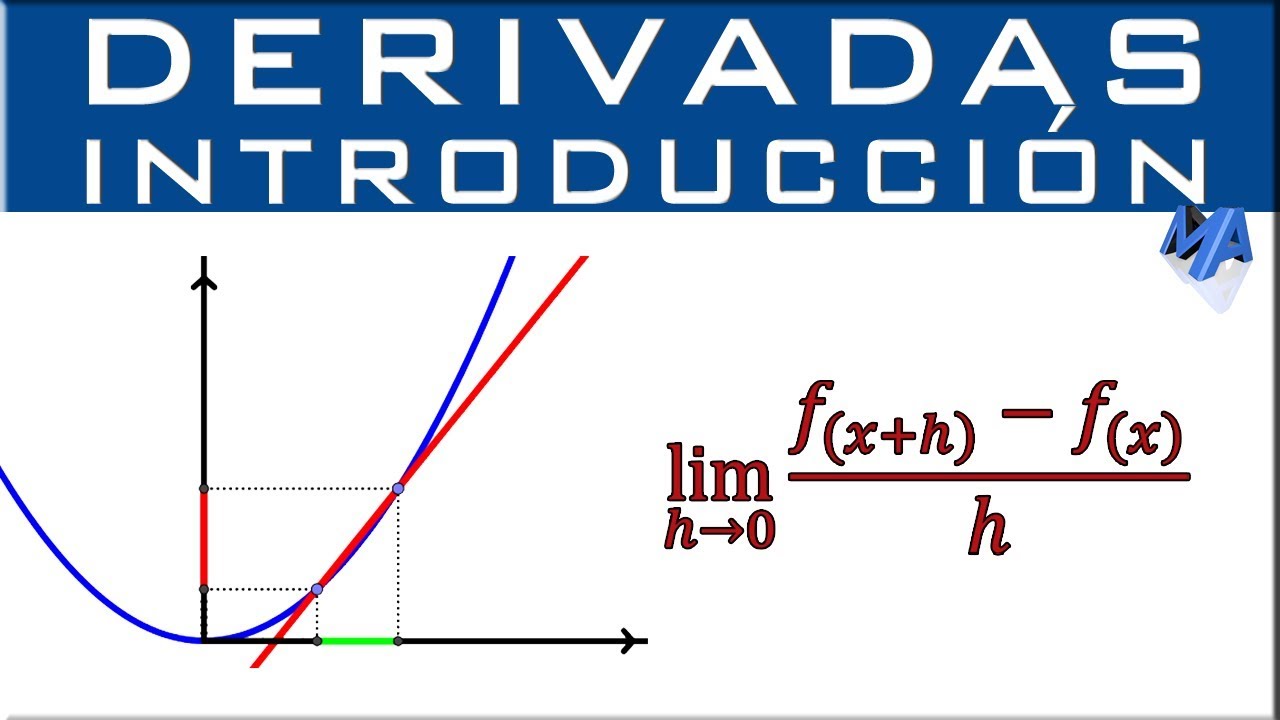
-La velocidad instantánea es la velocidad de una partícula en un punto específico del tiempo y se determina por la pendiente de la recta tangente a la gráfica posición-tiempo en ese punto.
¿Cuál es la velocidad instantánea de la partícula a los 2 segundos?
-La velocidad instantánea a los 2 segundos es de -3.7 metros por segundo, basada en la pendiente de la recta tangente a la gráfica en ese punto.
¿Cómo se encuentran los puntos que definen la recta tangente a la gráfica en el tiempo de 2 segundos?
-Los puntos que definen la recta tangente son los que cortan el eje del tiempo en 3.5 segundos y el eje de la posición en 0 metros.
¿Qué implica la pendiente de la recta tangente en términos de movimiento de la partícula?
-La pendiente de la recta tangente indica la tasa de cambio de posición con respecto al tiempo, es decir, la velocidad instantánea.
¿Por qué es importante calcular la velocidad instantánea en un punto específico del tiempo?
-Es importante porque nos da información sobre el comportamiento inmediato de la partícula en ese momento, lo que puede ser crucial para entender su movimiento.
¿Cómo se pueden representar matemáticamente la velocidad promedio y la velocidad instantánea?
-La velocidad promedio se representa como Δx/Δt y la velocidad instantánea como la derivada de la función posición con respecto al tiempo.

Outlines

00:00

📐 Cálculo de Velocidad Promedio y Instantánea

El vídeo comienza explicando un ejercicio relacionado con la física, específicamente con la velocidad promedio y la velocidad instantánea. Se describe cómo se calcula la velocidad promedio entre dos puntos dados en un gráfico de posición versus tiempo. Se menciona que la velocidad promedio es la pendiente de la línea que une esos dos puntos, y se calcula como la diferencia en la posición dividida por la diferencia en el tiempo. En este caso, la velocidad promedio entre los tiempos de 1.5 segundos y 4 segundos se calcula como (2 metros - 8 metros) / (4 segundos - 1.5 segundos), dando como resultado una velocidad promedio de -2.4 metros por segundo. Además, se explica cómo se determina la velocidad instantánea en un tiempo específico, que es la pendiente de la recta tangente a la gráfica en ese punto. Se utiliza la pendiente de una recta que corta el eje del tiempo en 3.5 segundos y el eje de la posición en 0 metros para encontrar la velocidad instantánea en 2 segundos, que se calcula como (0 metros - 13 metros) / (3.5 segundos - 2 segundos), dando un resultado de -3.7 metros por segundo.

Mindmap

Keywords

💡Velocidad promedio

La velocidad promedio es el cambio en la posición de un objeto dividido por el cambio correspondiente en el tiempo. Es una medida que nos permite entender el desplazamiento medio de un objeto durante un intervalo de tiempo específico. En el vídeo, se utiliza para calcular el desplazamiento de una partícula entre los tiempos de 1.50 segundos y 4 segundos, encontrando la pendiente de la recta que une los puntos de posición a esos tiempos.

💡Velocidad instantánea

La velocidad instantánea es la velocidad de un objeto en un punto específico de su trayectoria, esencialmente la velocidad a un instante de tiempo dado. Se relaciona con la derivada de la función posición con respecto al tiempo. En el vídeo, se busca la velocidad instantánea de la partícula a los 2 segundos, encontrando la pendiente de la recta tangente a la gráfica posición-tiempo en ese punto.

💡Posición

La posición es el punto en el espacio que ocupa un objeto en un momento dado. En física, se suele representar en una gráfica con el eje de las abscisas (generalmente el eje x). En el vídeo, la posición de la partícula se usa para calcular tanto la velocidad promedio como la instantánea a lo largo del tiempo.

💡Tiempo

El tiempo es una medida de la duración entre dos eventos y es fundamental en la física para describir el movimiento de los objetos. En el vídeo, el intervalo de tiempo dt de 1.50 segundos a 4 segundos se utiliza para calcular la velocidad promedio de la partícula.

💡Gráfica posición vs tiempo

Una gráfica de posición versus tiempo es una representación gráfica que muestra cómo la posición de un objeto cambia con el tiempo. Es una herramienta común en la física para analizar el movimiento. En el vídeo, se utiliza esta gráfica para identificar tanto la velocidad promedio como la instantánea de la partícula.

💡Derivada

La derivada es un concepto fundamental del cálculo que representa la tasa a la que una cantidad cambia con respecto a otra, como la velocidad con respecto al tiempo. En el vídeo, la derivada de la función posición-tiempo se menciona para explicar cómo se calcula la velocidad instantánea.

💡Pendiente

La pendiente es una medida de la inclinación de una línea en una gráfica, que representa el cambio en la variable y (en este caso, la posición) por el cambio en la variable x (el tiempo). En el vídeo, la pendiente se usa para calcular tanto la velocidad promedio como la instantánea.

💡Recta tangente

La recta tangente es una línea que toca la curva en un punto específico, y su pendiente es igual a la derivada de la función en ese punto. En el vídeo, la recta tangente a la gráfica en el tiempo de 2 segundos se utiliza para encontrar la velocidad instantánea de la partícula.

💡Partícula

Una partícula en física es un objeto que se estudia considerando solo su masa y posición, sin importar su tamaño o forma. En el vídeo, la partícula se usa para ejemplificar cómo calcular la velocidad promedio y instantánea.

💡Desplazamiento

El desplazamiento es la distancia que recorre un objeto desde su posición inicial hasta su posición final, sin importar el camino que haya seguido. En el vídeo, el desplazamiento se calcula como la diferencia de posición entre dos tiempos para encontrar la velocidad promedio.

💡Intervalo de tiempo

El intervalo de tiempo es la duración entre dos momentos específicos. Es crucial para calcular la velocidad promedio, ya que se divide el cambio en la posición por este intervalo de tiempo. En el vídeo, el intervalo de tiempo dt de 1.50 segundos a 4 segundos se utiliza para calcular la velocidad promedio.

Highlights

El vídeo trata sobre el cálculo de velocidad promedio y velocidad instantánea.

Se utiliza una gráfica posición vs tiempo para ilustrar el movimiento de una partícula.

El ejercicio pide calcular la velocidad promedio entre 1.50 segundos y 4 segundos.

La velocidad promedio se calcula como el cambio de posición dividido por el cambio de tiempo.

La posición de la partícula a los 1.5 segundos es 8 metros y a los 4 segundos es 2 metros.

La velocidad promedio se halla como la pendiente de la recta entre los puntos mencionados.

La velocidad promedio resulta en -2.4 metros por segundo.

Se pide también determinar la velocidad instantánea a los 2 segundos.

La velocidad instantánea se encuentra a partir de la pendiente de la recta tangente a la curva en el punto de interés.

La recta tangente en el tiempo de 2 segundos se determina por dos puntos dados.

Los puntos dados para la recta tangente son (0, 13) y (3.5, 0).

La pendiente de la recta tangente es la variación de posición dividida por la variación de tiempo.

La velocidad instantánea a los 2 segundos se calcula como -3.7 metros por segundo.

El vídeo invita a los espectadores a dejar dudas y opiniones en los comentarios.

Se agradece a los suscriptores y se les recuerda activar la notificación para nuevos vídeos.

El vídeo termina con la promesa de un nuevo vídeo próximamente.