Qué es la derivada? | Concepto de derivada

Matemáticas profe Alex

15 Mar 201810:42

Summary

TLDREn este video, se aborda el concepto de derivada en el contexto de la velocidad promedio y la velocidad instantánea. Se utiliza una competencia de autos para ilustrar la diferencia entre ambas. Se calcula la velocidad promedio de dos autos, uno azul y otro rojo, que compiten en un recorrido de 100 metros. A través de un gráfico de posición contra tiempo, se muestra cómo la inclinación de la línea representa la velocidad. Se destaca que la velocidad instantánea varía a lo largo del tiempo y se introduce el concepto de derivada como una herramienta para encontrar la velocidad en un punto específico. El video concluye con una explicación de cómo la derivada se relaciona con la recta tangente a una función dada, y se invita a los espectadores a explorar más sobre el tema en el canal del creador.

Takeaways

🏎️ La derivada es utilizada para encontrar la velocidad en un punto específico de una curva, lo que es esencial en el análisis de funciones y su comportamiento en diferentes puntos.
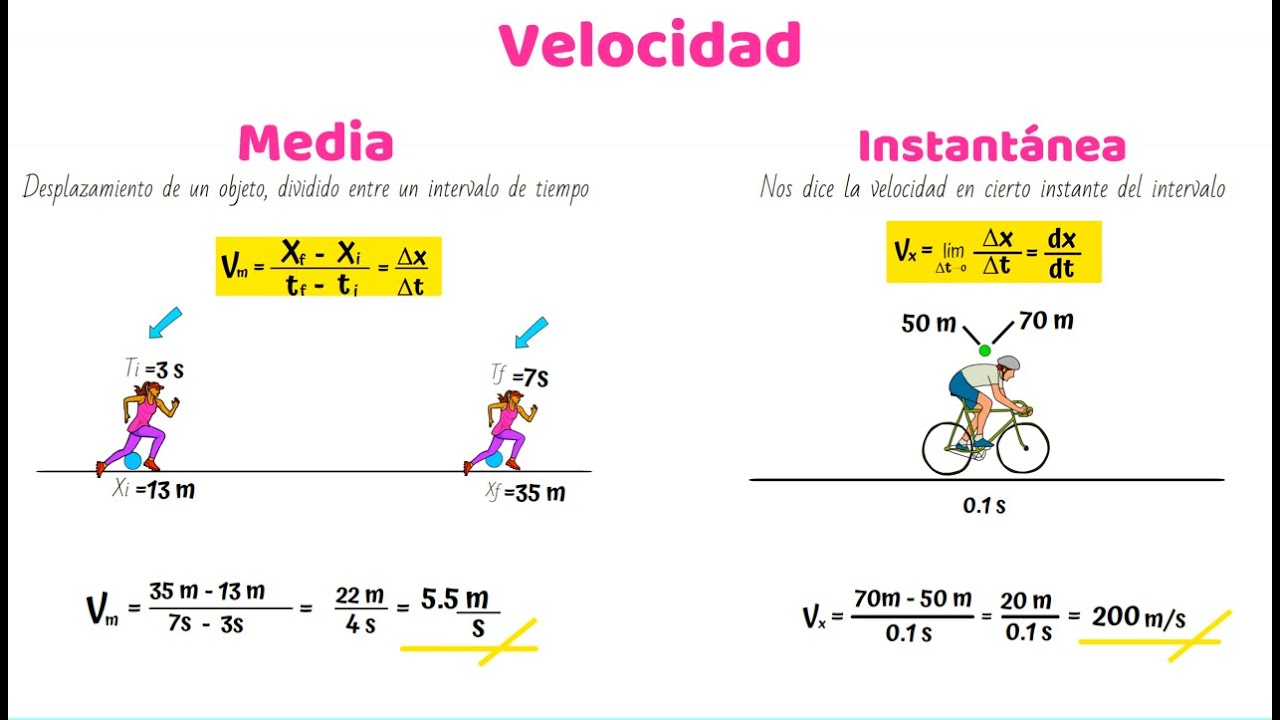
📈 La velocidad promedio se calcula dividiendo la distancia recorrida por el tiempo transcurrido, lo que permite comparar el rendimiento entre diferentes objetos o situaciones.
⏱️ La velocidad instantánea es diferente a la velocidad promedio, y es la velocidad exacta en un punto específico en tiempo, representada por la pendiente de la tangente a la curva en ese punto.
📊 Un gráfico de posición contra tiempo (también conocido como gráfico de espacio-tiempo) puede mostrar cómo varía la velocidad a lo largo del tiempo, indicando la aceleración o la desaceleración.
📌 La inclinación de la línea en un gráfico de velocidad vs. tiempo indica la velocidad de un objeto; una línea más inclinada significa una velocidad más alta.
🚀 Al inicio de un movimiento, la velocidad comienza en cero y aumenta gradualmente hasta alcanzar una velocidad máxima, representando un proceso de aceleración.
📐 La derivada se calcula tomando dos puntos cercanos en el gráfico y encontrando la pendiente de la línea que une esos puntos; a medida que los puntos se acercan, la aproximación a la derivada se vuelve más precisa.
🔍 El límite de la velocidad cuando el tiempo transcurrido entre dos puntos tiende a cero (h o Δx tiende a cero) es la definición matemática de la derivada en un punto específico.
🛣️ El concepto de derivada es fundamental en la física y las matemáticas para describir cambios en una variedad de contextos, incluida la cinemática y la modelización de sistemas dinámicos.
📋 La habilidad para calcular la derivada es esencial para comprender cómo las cosas cambian con el tiempo y para predecir comportamientos futuros en una amplia gama de disciplinas.
🎓 Aprender a calcular y entender las derivadas es una habilidad valiosa que puede abrir muchas puertas en el ámbito académico y profesional.

Q & A

¿Qué es la velocidad promedio?
-La velocidad promedio es el espacio recorrido por un objeto dividido por el tiempo que le tomó recorrer esa distancia. En el ejemplo, el auto rojo recorrío 80 metros en 5 segundos, lo que da una velocidad promedio de 16 metros por segundo.
¿Cómo se calcula la velocidad instantánea?
-La velocidad instantánea se calcula tomando el límite del cociente del cambio en la posición (Δx) entre el cambio en el tiempo (Δt) cuando este último tiende a cero. También se conoce como el concepto de derivada en matemáticas.
¿Por qué la línea del gráfico de velocidad contra tiempo es más inclinada para el auto azul que para el auto rojo?
-La línea es más inclinada para el auto azul porque este tiene una mayor velocidad promedio, lo que indica que recorrrió una distancia mayor en el mismo período de tiempo en comparación con el auto rojo.
¿Cómo se relaciona la aceleración con la curvatura en el gráfico de velocidad contra tiempo?
-Una curvatura más pronunciada en el gráfico de velocidad contra tiempo indica una aceleración más rápida. En el caso del auto azul, que aumentó su velocidad desde cero hasta su velocidad máxima, la curva se inclina más, mostrando una aceleración constante.
¿Cómo se define el punto Xy en el contexto de la derivada?
-El punto Xy es un punto específico en el gráfico que representa un instante en el tiempo (coordenada X) y la distancia recorrida en ese instante (coordenada Y). Se utiliza para calcular la velocidad instantánea en ese punto utilizando la derivada.
¿Qué es el incremento en el tiempo h?
-El incremento en el tiempo h es la diferencia de tiempo entre dos puntos en el gráfico. Se utiliza para calcular la velocidad entre dos puntos específicos al dividir el espacio recorrido por este intervalo de tiempo.
¿Cómo se calcula la velocidad exacta en un punto dado利用derivada?
-Para calcular la velocidad exacta en un punto dado, se toma el límite de la velocidad promedio cuando el intervalo de tiempo h tiende a cero. Esto se conoce como el límite de la derivada, y representa la pendiente de la tangente a la curva en el punto de interés.
¿Por qué la velocidad aparente de un objeto en movimiento no es siempre la misma durante todo su recorrido?
-La velocidad aparente de un objeto en movimiento no es siempre la misma porque el objeto puede acelerar o desacelerar a lo largo de su trayectoria. En el caso de los autos, empiezan con una velocidad de 0 y aumentan su velocidad hasta alcanzar una velocidad máxima.
¿Cómo se relaciona el concepto de derivada con la física?
-En física, la derivada se relaciona con la cinemática, donde se utiliza para calcular la velocidad instantánea de un objeto en movimiento, la aceleración, y otros parámetros dinámicos. La derivada de la posición con respecto al tiempo da la velocidad, y la derivada de la velocidad con respecto al tiempo da la aceleración.
¿Cómo se puede mejorar la precisión de la velocidad calculada entre dos puntos utilizando la derivada?
-La precisión de la velocidad calculada entre dos puntos se puede mejorar al reducir el intervalo de tiempo (h) considerado. A medida que h tiende a cero, la aproximación de la velocidad promedio se acerca al valor exacto de la velocidad instantánea en el punto de interés.
¿Por qué es importante el estudio de la derivada en matemáticas y física?
-El estudio de la derivada es importante porque proporciona una herramienta para modelar y predecir el comportamiento de sistemas en movimiento, entender cómo las cosas cambian con el tiempo y en respuesta a diferentes condiciones, y para optimizar procesos donde sea necesario encontrar el máximo o el mínimo de una función.

Outlines

00:00

🏎️ Concepto de Derivada y Velocidad Promedio y Instantánea

El primer párrafo introduce el curso de derivadas y establece la importancia de entender la velocidad promedio e instantánea para comprender la derivada. Se utiliza una competencia entre dos autos para ilustrar estos conceptos. El auto azul termina primero, recorriendo 100 metros en 5 segundos, mientras que el auto rojo solo recorre 80 metros en el mismo tiempo. A través de un gráfico de posición contra tiempo, se calcula la velocidad promedio de ambos autos y se observa cómo la inclinación de la línea representa la velocidad. Además, se menciona que la velocidad varía con el tiempo, y para encontrar la velocidad en un punto específico, se requiere el concepto de derivada.

05:02

📈 Derivada como Herramienta para Hallar Velocidad en un Punto Específico

El segundo párrafo profundiza en el concepto de derivada como una herramienta para calcular la velocidad en un punto específico en lugar de una promedio general. Se describe un método para encontrar la velocidad exacta en un punto dado, utilizando dos puntos y el tiempo transcurrido entre ellos, denominado 'h' o el incremento de tiempo. A través de un ejemplo, se muestra cómo aproximar la velocidad instantánea al acercar el segundo punto hacia el primero hasta que el tiempo transcurrido entre ellos se acerca a cero, lo que se conoce como el límite. Se resalta que la derivada representa la velocidad exacta en un punto y es la pendiente de la recta tangente a una función en ese punto.

10:07

📚 Conclusión y Recursos para Aprender Más sobre Derivadas

El tercer párrafo concluye la explicación de la derivada y su importancia para encontrar la velocidad en un punto exacto. El hablante alienta a los espectadores a que visiten su canal o sigan el enlace proporcionado en la descripción del video para acceder al curso completo de derivadas. Finalmente, se hace un llamado a la acción para que los espectadores se suscriban, comenten, compartan y den like al video, antes de despedirse.

Mindmap

Keywords

💡Derivada

La derivada es una operación matemática utilizada para encontrar la velocidad o la tasa de cambio de una función en un punto específico. En el video, se relaciona con la idea de la velocidad instantánea de un objeto en movimiento, como un automóvil en una carrera. La derivada se calcula tomando el límite de la velocidad promedio cuando el intervalo de tiempo considerado se acerca a cero.

💡Velocidad Promedio

La velocidad promedio se refiere a la distancia total recorrida dividida por el tiempo total transcurrido. En el contexto del video, se utiliza para comparar la distancia recorrida por dos autos en un lapso de tiempo determinado, siendo fundamental para entender la introducción a la velocidad instantánea y la derivada.

💡Velocidad Instantánea

La velocidad instantánea es la velocidad de un objeto en un momento exacto. Se diferencia de la velocidad promedio en que no toma en cuenta el cambio de velocidad a lo largo del tiempo. En el video, se ilustra cómo la derivada puede ser usada para encontrar la velocidad instantánea de un automóvil en un punto específico del tiempo.

💡Incremento de Tiempo (h)

El incremento de tiempo, representado por 'h' en el video, se refiere a la diferencia entre dos puntos de tiempo mientras se calcula la velocidad instantánea. Es un concepto clave en la derivada, ya que al acercar 'h' a cero, se obtiene la velocidad exacta en un punto específico.

💡Función

Una función en matemáticas es una relación que asigna a cada elemento de un conjunto (dominio) un único elemento del conjunto de destino (rango). En el video, la función puede representar la posición de un objeto en el espacio en función del tiempo, y se utiliza para graficar y calcular la derivada.

💡Gráfico de Posición contra Tiempo

Este gráfico muestra cómo la posición de un objeto cambia con el tiempo. En el video, se utiliza para visualizar la distancia recorrida por los autos y cómo esta información puede ser usada para calcular la velocidad promedio y, eventualmente, la velocidad instantánea a través de la derivada.

💡Recta Tangente

La recta tangente a una curva en un punto dado es la línea que toca la curva en ese punto y que tiene la misma dirección que la curva en ese punto. En el video, la recta tangente representa la velocidad instantánea a un punto específico de la trayectoria de un objeto.

💡Límite

En matemáticas, un límite describe el valor que una función o secuencia asume cuando su argumento se acerca a cierto valor. En el contexto de la derivada, el límite se utiliza para definir la velocidad instantánea tomando el límite del cociente de los cambios cuando el intervalo de tiempo tiende a cero.

💡Aceleración

La aceleración es la tasa de cambio de la velocidad. En el video, se discute cómo los autos cambian su velocidad a medida que compiten, y cómo la derivada puede ser utilizada para encontrar la tasa de cambio de la velocidad, es decir, la aceleración, en un punto específico.

💡Cálculo Diferencial

El cálculo diferencial es una rama del álgebra que se enfoca en el estudio de las derivadas y sus aplicaciones. En el video, el cálculo diferencial se utiliza para analizar cambios sutiles en la velocidad de los autos y para calcular la velocidad instantánea en un punto específico del tiempo.

💡Tasa de Cambio

La tasa de cambio describe la rapidez con la que una cantidad cambia respecto a otra. En el video, la tasa de cambio es fundamental para entender cómo la velocidad de un objeto cambia con el tiempo, y cómo la derivada puede ser usada para medir esa tasa de cambio en un instante específico.

Highlights

Introducción al concepto de derivadas y su importancia en la comprensión de la velocidad promedio y la velocidad instantánea.

Descripción de una competencia entre dos carros para ilustrar la diferencia entre velocidad promedio y velocidad instantánea.

Explicación de cómo se calcula la velocidad promedio utilizando el espacio recorrido y el tiempo transcurrido.

Representación gráfica de la velocidad promedio a través de un gráfico de posición contra tiempo.

Diferencia entre la línea de velocidad del carro azul y el carro rojo en la gráfica, indicando la diferencia de velocidades.

La inclinación de la línea en la gráfica como indicativo de la velocidad del vehículo.

Ejemplo numérico de cómo se calcula la velocidad promedio para el carro rojo y el carro azul.

Importancia del concepto de derivada para encontrar la velocidad en un punto específico en lugar de la velocidad promedio.

Método para calcular la velocidad instantánea a partir de dos puntos utilizando el cambio en el espacio y el tiempo.

La derivada como herramienta para encontrar la velocidad exacta en un punto dado, representando la recta tangente a la curva.

Proceso para aproximar la velocidad instantánea al acercar el segundo punto hacia el primero hasta que el tiempo transcurrido entre ellos tenga un valor cercano a cero.

Explicación de cómo la velocidad calculada en un punto específico se convierte en la velocidad exacta cuando el incremento de tiempo tiende a cero.

Representación de la velocidad instantánea como el límite del cociente del cambio en el espacio y el cambio en el tiempo cuando este último tiende a cero.

La derivada como concepto fundamental en el análisis de funciones y la física para describir cambios rápidos y aceleraciones.

Invitación a los espectadores a suscribirse, comentar, compartir y activar la notificación para no perderse de más contenido educativo.

Disponibilidad del curso completo de derivadas en el canal del profesor o a través del enlace proporcionado.