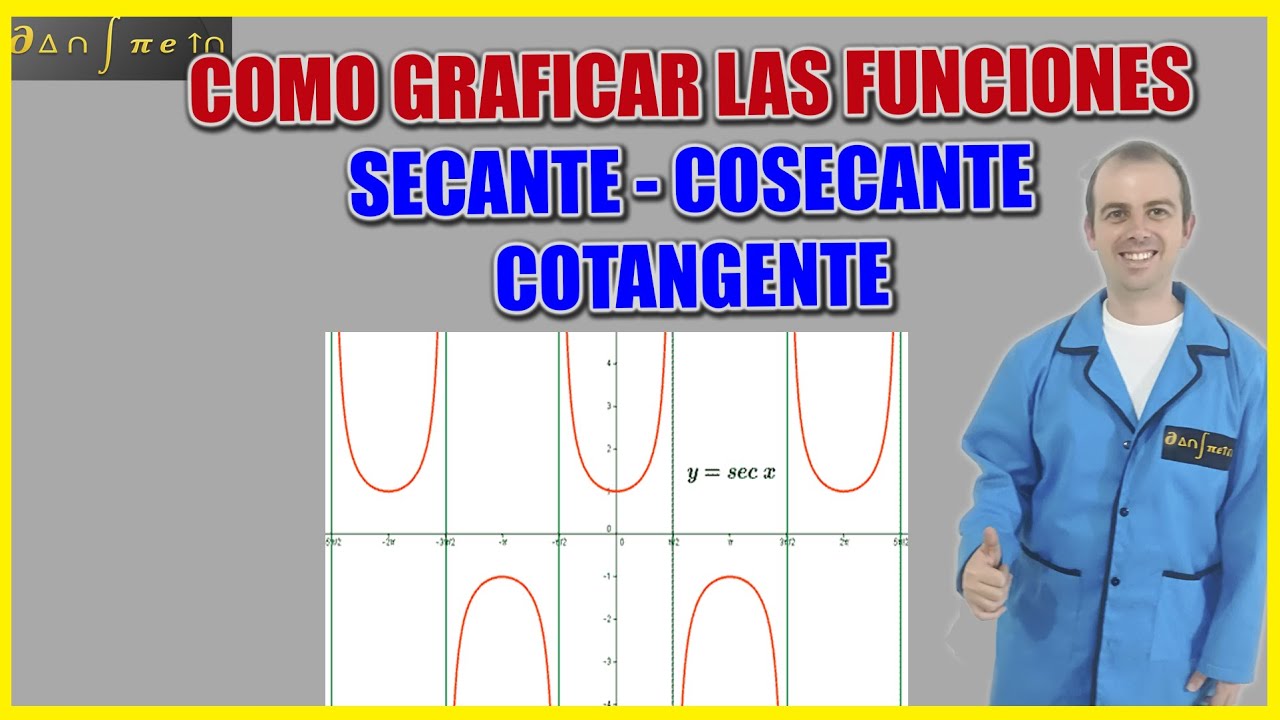
Grafica de función secante
Summary
TLDREn este video se explica cómo graficar la función secante, que es la inversa de la función coseno. Se utiliza una circunferencia unitaria centrada en el origen del plano cartesiano para representar los ángulos y calcular las líneas trigonométricas de la secante. La explicación detalla cómo dividir la circunferencia en ángulos y cómo determinar los valores de la secante en diferentes cuadrantes, resaltando la positividad o negatividad de la función según el cuadrante. Se destaca la importancia de las asíntotas y la periodicidad de la función, que se repite cada 360 grados.
Takeaways
- 📐 La función secante es la función inversa de la función coseno.
- 🔴 Se usa una circunferencia concéntrica unitaria para representar la función secante en el plano cartesiano.
- 🔵 La circunferencia se divide en múltiplos de cuatro, ocho, doce, etc., para encontrar ángulos representativos.
- 📏 Se definen rectas paralelas al eje Y para representar la secante en los primeros y cuartos cuadrantes.
- 📈 La secante es positiva en los primeros y cuartos cuadrantes y negativa en los segundos y terceros.
- 📉 En los ángulos de 90 y 270 grados, la función secante es indefinida y representa asíntotas en la gráfica.
- 🔢 El valor de la secante de 45 grados se calcula como raíz cuadrada de 2, aproximadamente 1.41.
- 📌 La secante de 0 grados da como resultado el valor de 1, ya que es el radio de la circunferencia.
- 🔄 La gráfica de la función secante se repite cada 360 grados, indicando que tiene un periodo de 360 grados.
- ➡️ La gráfica de la función secante no está definida para valores entre -1 y 1, y tiene una amplitud desde menos infinito hasta -1 y desde 1 hasta infinito.
Q & A
¿Qué es la función secante en trigonometría?
-La función secante es la función inversa de la función coseno.
¿Cuál es la relación entre la función secante y la circunferencia concéntrica?
-La circunferencia concéntrica es utilizada para representar gráficamente la función secante, donde el radio de la circunferencia es unitario y el centro está en el origen del plano cartesiano.
¿Por qué se divide la circunferencia en múltiplos de cuatro?
-La circunferencia se divide en múltiplos de cuatro porque está representada en el plano cartesiano, que a su vez está dividido en cuatro cuadrantes.
¿Cuál es el ángulo que representa cada división si la circunferencia se divide en 8 partes?
-Si la circunferencia se divide en 8 partes, cada división representa un ángulo de 45 grados.
¿Cómo se determina si la secante es positiva o negativa en los diferentes cuadrantes?
-La secante es positiva en los primeros y cuartos cuadrantes, y negativa en los segundos y terceros cuadrantes, basándose en la proyección del coseno en el eje X.
¿Qué es una recta paralela al eje Y que es tangente a la circunferencia?
-Es una recta que tiene un punto común con la circunferencia y es paralela al eje Y, utilizadas para determinar las líneas trigonométricas de la función secante en los primeros y cuartos cuadrantes.
¿Cuál es el valor numérico de la secante de 45 grados?
-La secante de 45 grados es igual a la raíz cuadrada de 2, que es aproximadamente 1.41.
¿Qué ocurre con la función secante en los ángulos de 0 grados y 180 grados?
-La función secante en 0 grados y 180 grados es indefinida, ya que no hay intersección con la circunferencia para estos ángulos.
¿Cómo se representa gráficamente la secante en los ángulos de 90 grados y 270 grados?
-En los ángulos de 90 grados y 270 grados, la función secante se representa como una línea asíntota, que es una línea que se acerca pero nunca se intersecta con la gráfica.
¿Cuál es el periodo de la función secante?
-El periodo de la función secante es de 360 grados, es decir, se repite cada 360 grados.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)