Solución de límites por factorización | Ejemplo 10
Summary
TLDREn este video se explica cómo resolver límites utilizando la factorización de trinomios de la forma \(x^2 + bx + c\). El instructor guía a los espectadores a través de un ejercicio paso a paso, mostrando dos métodos de factorización para diferentes tipos de trinomios. Además, se aborda la indeterminación y cómo eliminarla al factorizar, todo con un enfoque práctico y directo. Al final, se deja un ejercicio para que los espectadores practiquen, y se invita a revisar videos anteriores sobre límites y factorización para quienes necesiten más apoyo.
Takeaways
- 📘 Este video forma parte de un curso de límites y enseña cómo resolver límites mediante factorización.
- 🔢 Se aborda la factorización de trinomios de la forma \(x^2 + bx + c\) y \(x^2 + bx - c\), donde la diferencia radica en la presencia de un signo más o menos ante el término medio.
- 📐 Se explica que si el trinomio tiene \(x^2\) sin coeficiente, se entiende que es \(x^2\).
- ✅ Se recomienda verificar si la ecuación se puede resolver simplemente reemplazando el valor antes de intentar factorizar.
- 🔄 Se practica la factorización de trinomios ordenando primero los términos y luego buscando dos números que cumplan con ciertas condiciones de multiplicación y suma o resta.
- 📝 Se menciona la importancia de recordar la indeterminación en límites, como \(x^2 - 5\), y cómo buscar un paréntesis que lo resuelva.
- 📖 Se sugiere que si hay dudas en factorización, se revisen los videos anteriores sobre límites y factorización.
- 👉 Se enfatiza la necesidad de factorizar trinomios de forma separada para evitar confusiones.
- 🔢 Se detalla el proceso de factorización paso a paso, incluyendo la multiplicación de coeficientes y la búsqueda de números que cumplan con condiciones específicas.
- 🔄 Se muestra cómo simplificar la factorización al final, extrayendo factores comunes y resolviendo la indeterminación.
- 📑 Se invita a los estudiantes a practicar con ejercicios similares y se ofrecen recursos adicionales para aprender más sobre límites.
Q & A
¿Qué métodos de factorización se discuten en el curso de límites y factorización?
-Se discuten dos métodos de factorización: el trinomio de la forma x^2 + bx + c y el trinomio de la forma x^2 + bx - c.
¿Cuál es la diferencia clave entre los trinomios x^2 + bx + c y x^2 + bx - c?
-La diferencia clave es el signo que acompaña al término medio: el primero tiene una suma (+), mientras que el segundo tiene una resta (-).
¿Cómo se determina si un trinomio puede ser factorizado fácilmente?
-Se verifica si el trinomio tiene la forma x^2 + bx + c o x^2 + bx - c, y si el término que acompaña a x^2 no tiene coeficiente, es decir, es implícito un 1.
¿Qué es la indeterminación en el contexto de los límites?
-La indeterminación se refiere a una expresión que parece no tener una solución clara, como 0/0 o infinito/infinito, que se resuelve al factorizar y simplificar.
¿Cómo se factoriza un trinomio de la forma x^2 + bx + c?
-Se buscan dos números que, al multiplicarse, den el término constante (c) y, al sumarse, den el término de la x (b). Estos números se colocan en dos paréntesis, con el signo correcto en cada uno.
¿Cuál es el primer paso al factorizar un trinomio x^2 + bx - c?
-Es el mismo que para x^2 + bx + c: buscar dos números que multiplicados den el término constante y que sumados den el término de la x.
¿Cómo se identifica la indeterminación en una expresión algebraica?
-Se identifica al observar que la expresión se vuelve de la forma 0/0 o infinito/infinito, lo cual indica que es necesario factorizar y simplificar.
¿Qué significa el signo más y el signo menos en la factorización de trinomios?
-El signo más en el primer paréntesis indica que ambos factores en ese paréntesis son positivos o ambos negativos. El signo menos en el segundo paréntesis indica que uno es positivo y el otro negativo.
¿Cómo se determina el número a colocar en el primer paréntesis al factorizar un trinomio?
-Se coloca el número más grande de los dos que multiplicados dan el término constante y que sumados dan el término de la x.
¿Cuál es la importancia de reemplazar la x con el número dado al resolver un límite?
-Es crucial para encontrar el valor del límite específico, ya que después de simplificar y eliminar la indeterminación, permite evaluar el límite cuando x tiende al número dado.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Solución de límites por factorización | Ejemplo 3

Solución de límites por factorización | Ejemplo 4
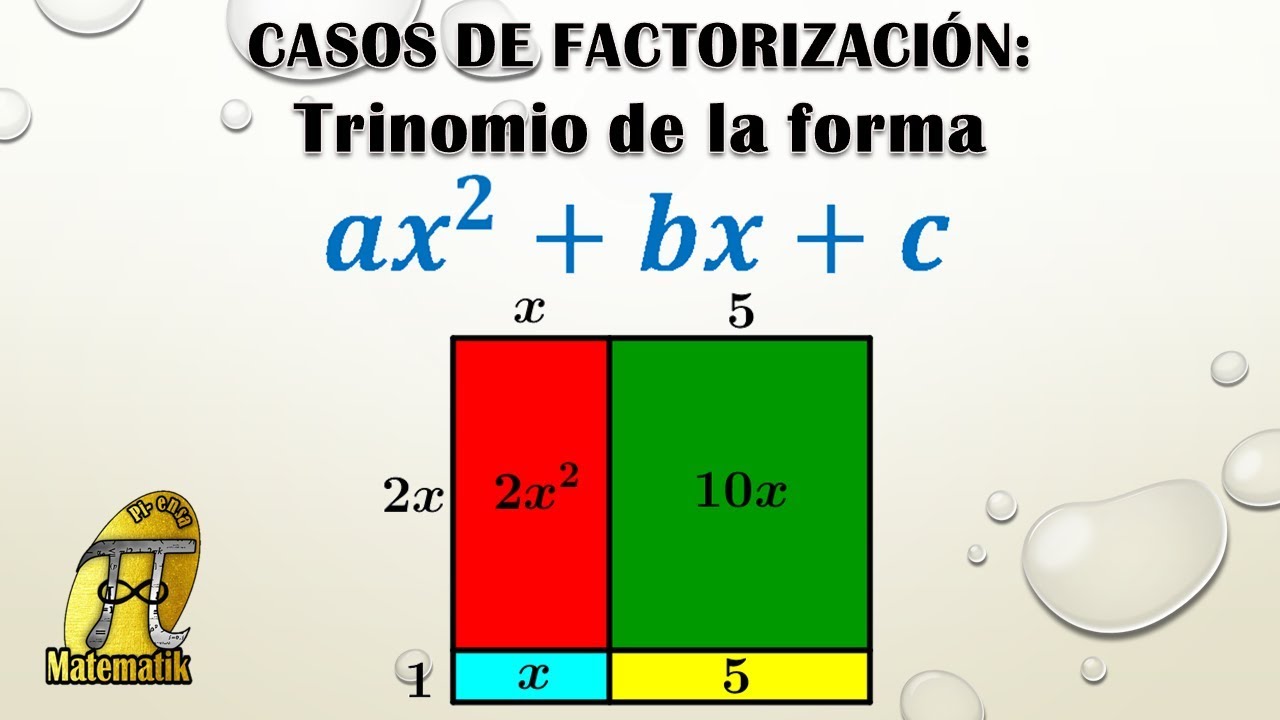
Trinomio de la forma ax^2+bx+c gráficamente | Casos de Factorización

LOS 10 CASOS DE FACTORIZACION En 10 minutos Cursos online

Factorización Trinomio de la forma ax2+bx+c | Paso a paso

Solución de límites por factorización | Ejemplo 6
5.0 / 5 (0 votes)
