Metodo de Newton-Raphson | Explicación y ejercicio resuelto

FísicayMates

18 Sept 201414:13

Summary

TLDRThis video from the Physics and Math channel offers a detailed and easy-to-understand explanation of Newton-Raphson method, a powerful technique for finding roots of equations. The host walks viewers through the method's definition, its iterative nature, and its geometric interpretation. A step-by-step demonstration is provided, starting with an initial guess close to the root, followed by successive approximations using the derivative of the function. The video includes a practical example, where the method is applied to find an approximate root of a given function, showcasing how quickly the approximations converge to the actual root. The host emphasizes the importance of accurate calculations with each iteration to achieve a precise result.

Takeaways

📚 The video is an educational tutorial explaining the Newton-Raphson method in detail, a technique used to find the roots of equations.
🔍 The main objective of the Newton-Raphson method is to estimate the solution of an equation \( F(x) = 0 \) by producing a sequence of approximations that get closer to the solution.
📈 The method involves selecting an initial guess \( x_0 \) close to the root and then iteratively refining this guess using the method's formula.
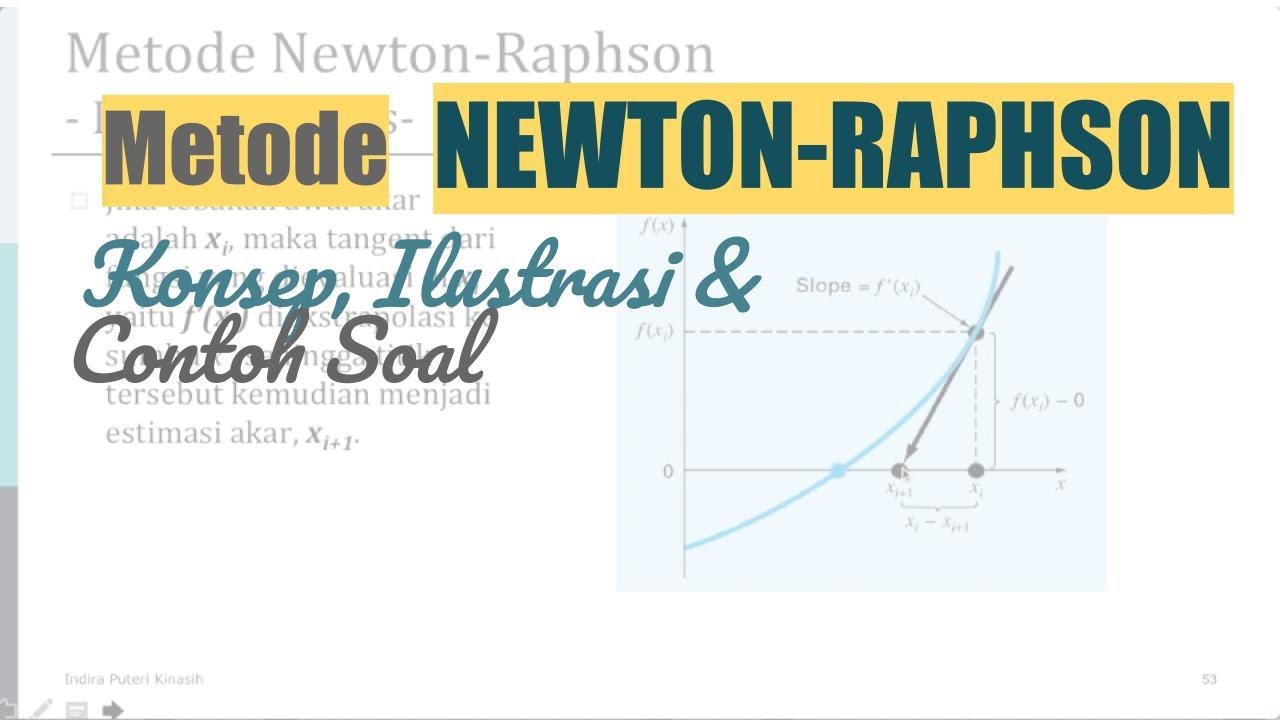
📝 A geometric explanation of the method is provided, where the tangent line to the function at a point is used to find the next approximation.
📉 The iterative process is demonstrated graphically, showing how starting from \( x_0 \), the method quickly converges to the root with just a few iterations.
👨‍🏫 The tutorial includes a step-by-step guide on how to apply the Newton-Raphson method, starting with an initial guess and using the formula to find subsequent approximations.
📚 An analytical explanation is given on how to use the method with numbers, emphasizing the importance of using the first approximation to find the second, and so on.
🔢 The video includes a practical example problem where the method is applied to find an approximation of a root for a given function, starting with \( x = 1 \).
📉 A graphical representation of the function and its root is provided to help viewers understand the starting point and the iterative process visually.
🔄 The iterative formula used in the Newton-Raphson method is explained and demonstrated through the calculation of successive approximations.
📝 The difficulty of the method is highlighted, noting that it requires careful substitution of values into the function and its derivative for accurate results.

Q & A

What is the objective of the Newton-Raphson method?
-The objective of the Newton-Raphson method is to estimate the solution of an equation F(x) = 0 by finding the roots of the equation through successive approximations.
How do we start the Newton-Raphson method?
-We start the Newton-Raphson method by choosing an initial guess x₀, which is a number close to the root.
What are the iterations in the Newton-Raphson method?
-Iterations in the Newton-Raphson method are successive approximations that move closer to the root with each step.
What is the geometric explanation of the Newton-Raphson method?
-Geometrically, the method involves drawing a tangent line at the initial point and finding its intersection with the x-axis. This process is repeated with each new point until the approximation is close enough to the actual root.
How do we perform the first iteration in the Newton-Raphson method?
-The first iteration is performed by taking the initial guess x₀, calculating the tangent at this point, and finding the intersection with the x-axis to get the next approximation x₁.
What is the formula used in the Newton-Raphson method?
-The formula used is xₙ₊₁ = xₙ - f(xₙ) / f'(xₙ), where xₙ is the current approximation, f(xₙ) is the function value at xₙ, and f'(xₙ) is the derivative value at xₙ.
What is the significance of the derivative in the Newton-Raphson method?
-The derivative helps determine the slope of the tangent line at each approximation point, which is crucial for calculating the next approximation.
How do we know when to stop iterating in the Newton-Raphson method?
-We stop iterating when the successive approximations are sufficiently close to the actual root, usually determined by a predefined tolerance level.
What example function is used in the video to illustrate the Newton-Raphson method?
-The example function used is x³ - x - 1 = 0.
What initial guess is used in the video example, and what root does it approximate?
-The initial guess used in the video example is x₀ = 1, and it approximates the root to be around 1.32 after several iterations.

Outlines

00:00

📚 Introduction to Newton-Raphson Method

The script begins with an introduction to the Newton-Raphson method, a numerical technique for finding successively better approximations to the roots (or zeroes) of a real-valued function. The method uses an iterative approach, starting with an initial guess that is close to the actual root. The process involves drawing tangent lines to the function's graph at the current approximation point and finding where these tangents intersect the x-axis to get the next approximation. The script explains that the method aims to produce a sequence of iterations that converge to the solution of an equation f(x) = 0.

05:02

🔍 Applying the Newton-Raphson Method to a Specific Problem

The second paragraph delves into applying the Newton-Raphson method to a specific mathematical problem. The function given is f(x) = x^3 - x - 1, and the initial guess for the root is x = 1. The script outlines the steps to calculate the derivative of the function, which is necessary for the iterative process. It demonstrates the first iteration using the formula x1 = x0 - f(x0) / f'(x0), where x0 is the initial guess. The explanation includes the calculation of the function and its derivative at x0, and how to use these to find x1, the first approximation of the root.

10:03

📉 Iterative Process and Convergence in Newton-Raphson Method

This paragraph continues the iterative process, illustrating how to refine the approximation of the root through subsequent iterations. It shows the calculations for the second and third iterations, emphasizing the importance of accuracy in substitution and arithmetic operations. The script points out that the method converges quickly, with the third iteration already providing a relatively good approximation of the root. It also highlights the increasing precision with each iteration, noting that by the fourth and fifth iterations, the root is approximated to two decimal places, concluding that the root is approximately 1.32.

Mindmap

Keywords

💡Newton-Raphson Method

The Newton-Raphson method is an iterative numerical technique used to find the roots of a real-valued function. In the context of the video, it is the main theme and is explained as a way to estimate the solution of an equation by producing a sequence of approximations that converge to the root. The script uses this method to find a good approximation of a root of a given function, starting with an initial guess and iteratively refining the estimate.

💡Root

In mathematics, a root of a function is the value for which the function equals zero. The video script discusses the goal of the Newton-Raphson method, which is to find the roots of equations, illustrating this with a specific function where the root is graphically represented as the intersection of the function with the x-axis.

💡Iteration

An iteration in the context of the Newton-Raphson method refers to each step in the sequence of approximations. The script mentions that each approximation is called an iteration, and the process involves starting with an initial guess and then using the method to successively improve the estimate until it is close enough to the actual root.

💡Derivative

The derivative of a function is a measure of the rate at which the function's value changes as its argument changes. In the script, the derivative is essential for the Newton-Raphson method as it is used to calculate the slope of the tangent line to the function at a given point, which is then used to find the next approximation of the root.

💡Tangent Line

A tangent line touches a curve at a single point without crossing it. In the video, the geometric interpretation of the Newton-Raphson method involves drawing a tangent line to the function at the current approximation point and finding where this line intersects the x-axis to get the next approximation.

💡Approximation

An approximation in this context is an estimate that is close to the true value but not exact. The script explains that the Newton-Raphson method starts with an initial approximation and improves it through iterations, getting closer to the actual root with each step.

💡Graphical Interpretation

The script provides a graphical interpretation of the Newton-Raphson method, showing how the method can be visualized by plotting the function and drawing tangent lines to estimate the root. This visual representation helps in understanding the iterative process of getting closer to the root.

💡Function

In mathematics, a function is a relation between a set of inputs and a set of permissible outputs. The video script uses a specific function, f(x) = x^3 - x - 1, to demonstrate the application of the Newton-Raphson method. The function is central to the process as the method is used to find its root.

💡Geometric

The term 'geometric' in the script refers to the visual or shape-related aspects of the Newton-Raphson method. The geometric explanation helps to understand how the method works by observing the graphical representation of the function and the tangent lines drawn at each iteration.

💡Precision

Precision in this context refers to the degree of exactness of an approximation. The script discusses how the Newton-Raphson method can be used to achieve a certain level of precision, with the example showing that after several iterations, the method provides an approximation of the root with two decimal places of accuracy.

Highlights

Introduction to the Newton-Raphson method for finding roots of equations.

The method aims to produce a sequence of approximations that approach the solution.

Explanation of the iterative process starting with an initial guess close to the root.

Geometric interpretation of the Newton-Raphson method using a tangent line to the function graph.

Graphical demonstration of the method's convergence to the root with successive iterations.

The importance of choosing a good initial guess to speed up convergence.

Analytical steps of the Newton-Raphson method using the formula for successive approximations.

Example problem to demonstrate the calculation procedure of the method.

Derivative calculation required for the Newton-Raphson formula application.

Iterative process illustrated with a specific function to find a root using the method.

Graphical observation of the root's location and the rationale for choosing the starting point.

Detailed calculation steps for the first few iterations of the method.

Observation of the method's convergence with each iteration getting closer to the root.

The challenge of the method lies in accurately substituting values into the function and its derivative.

Final approximation of the root with an accuracy of two decimal places after several iterations.

Conclusion of the method's effectiveness and the practicality of stopping at a certain level of precision.

Encouragement for viewers to like, subscribe, and share the video for further support.