Mass swinging in a horizontal circle | Centripetal force and gravitation | Physics | Khan Academy
Summary
TLDRThis tutorial explores a centripetal force problem involving a mass swinging in a horizontal circle on a string. It emphasizes the importance of understanding centripetal force concepts and outlines a strategy to solve such problems. The video teaches how to draw a force diagram, apply Newton's second law in one direction to find tension, and then use it to calculate the mass's speed. Key takeaways include the difference between tension and rope length and the correct application of trigonometry to find the circular path's radius.
Takeaways
- 🔍 **Understanding Centripetal Force**: The video emphasizes the importance of understanding centripetal force for solving physics problems involving circular motion.
- 📐 **Drawing a Force Diagram**: A key strategy is to draw a force diagram to visualize all forces acting on the object, including gravity and tension.
- 🧭 **Applying Newton's Second Law**: Use Newton's second law in one direction at a time, starting with the vertical direction to find tension.
- ⚖️ **Calculating Tension**: Tension in the rope can be calculated using the formula T = (mg)/(cos(θ)), where m is mass, g is gravity, and θ is the angle with the vertical.
- 📉 **Zero Vertical Acceleration**: The mass does not change its vertical position, so the vertical acceleration is zero, simplifying calculations.
- 🔄 **Horizontal Acceleration**: The horizontal acceleration is centripetal, given by ac = (v²)/r, where v is the speed and r is the radius of the circular path.
- 🔄 **Centripetal Force**: The horizontal component of tension provides the centripetal force necessary for circular motion.
- 📏 **Radius of Circular Path**: The radius of the circular path is not the length of the rope but can be found using r = Lsin(θ), where L is the rope's length.
- 🔢 **Calculating Speed**: The speed of the mass can be calculated using the formula v = √((Tsin(θ)·Lsin(θ))/m), incorporating the tension, rope length, and mass.
- 📋 **Conceptual Clarity**: The video stresses the importance of having a clear understanding of the terms and concepts involved in centripetal force problems.
Q & A
What is the scenario described in the video script?
-The scenario involves a mass tied to a string that is secured to the ceiling, with the mass swinging in a horizontal circle due to an initial velocity given to it.
What are the two main questions posed in the script?
-The two questions are: 1) What is the tension in the rope? 2) What has to be the speed of the mass?
What is the mass and length of the rope given in the problem?
-The mass is given as three kilograms and the length of the rope is two meters.
What is the angle made by the rope with respect to the vertical line?
-The rope makes an angle of thirty degrees with respect to the vertical line.
What is the strategy suggested for solving centripetal force problems?
-The strategy suggested is to first draw a quality force diagram for the object and then use Newton's second law for one direction at a time.
Why is it important to choose the right direction when applying Newton's second law?
-Choosing the right direction is important because if there are too many variables, it may not be solvable. If the chosen direction does not work out, the other direction should be tried.
What is the acceleration in the vertical direction for the mass moving in a horizontal circle?
-The acceleration in the vertical direction is zero because the mass is not changing its vertical height and is maintaining a constant height.
How is the vertical component of the tension (Ty) related to the total tension (T)?
-The vertical component of the tension (Ty) is related to the total tension (T) by the cosine of the angle the rope makes with the vertical line, which is thirty degrees.
What is the formula to calculate the tension in the rope?
-The tension in the rope (T) is calculated as the force of gravity (mg) divided by the cosine of thirty degrees.
What is the speed of the mass found to be?
-The speed of the mass is found to be approximately 2.4 meters per second.
Why is it incorrect to use the length of the rope as the radius in the centripetal force calculation?
-It is incorrect because the radius in the centripetal force calculation refers to the radius of the circular path the object is moving in, not the length of the rope itself.
How is the actual radius of the circular path determined?
-The actual radius of the circular path is determined by multiplying the length of the string (L) by the sine of the angle (30 degrees).
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

What Is Circular Motion? | Physics in Motion

Understanding Circular Motion
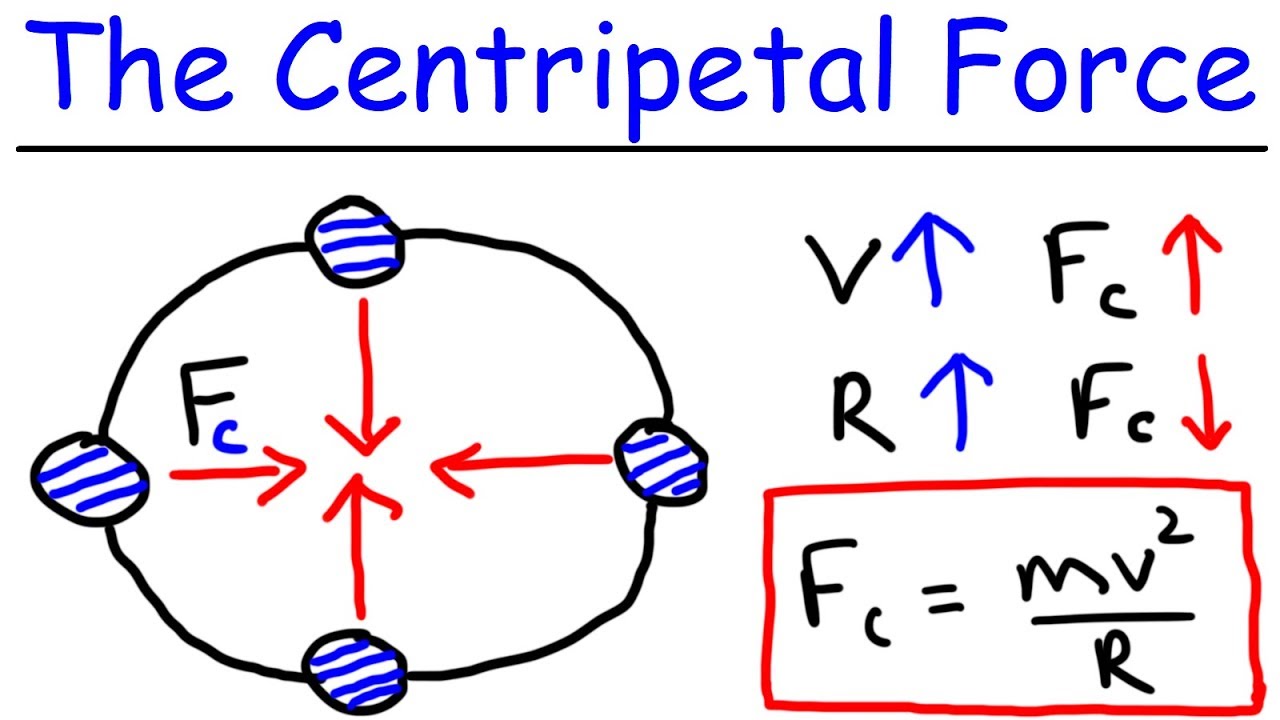
Physics - What Is a Centripetal Force?
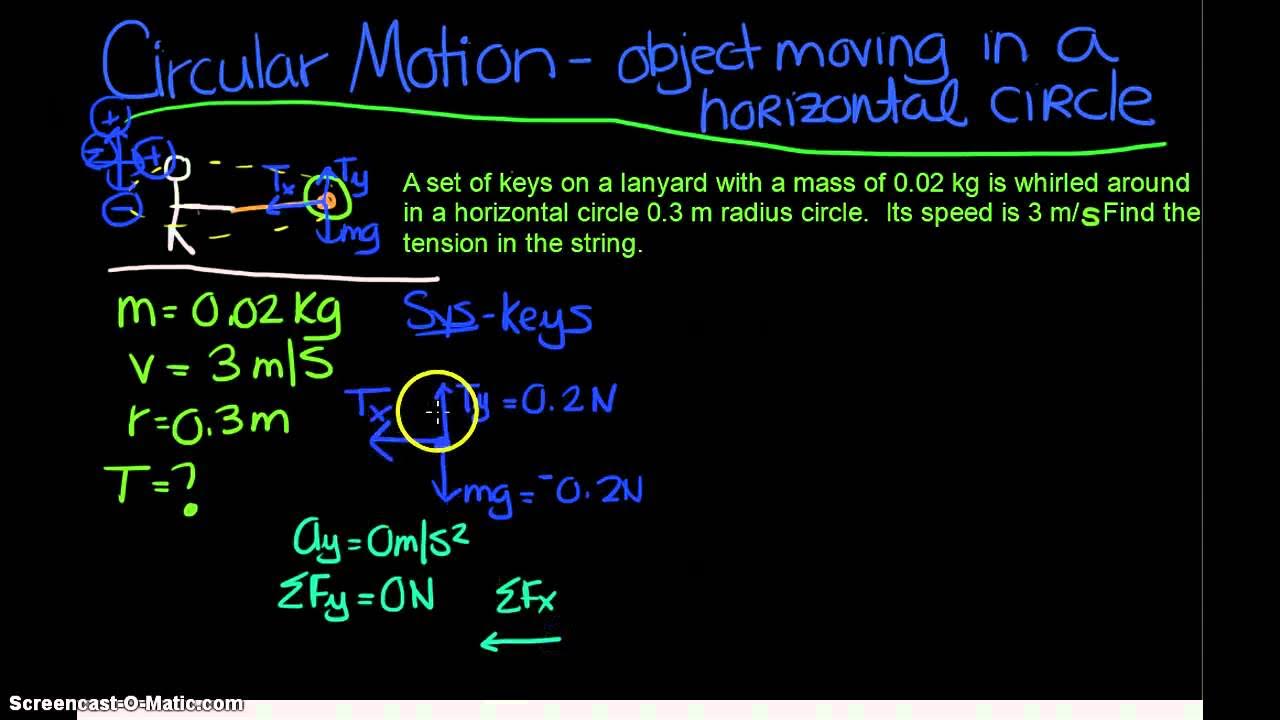
AP Physics 1: Circular Motion 3: Object moving in a horizontal circle

Centripetal force and acceleration intuition | Physics | Khan Academy

Quipper Video - Fisika - Gerak Melingkar Beraturan - Kelas 10
5.0 / 5 (0 votes)