Linear Transformations Vertical and Horizontal Stretching and Compressing Examples
Summary
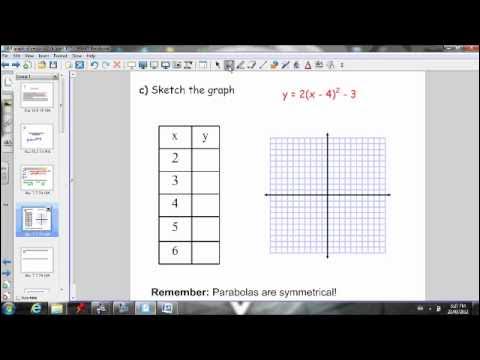
TLDRThis video explains how to horizontally and vertically stretch functions. It walks through examples, first demonstrating how to horizontally stretch a function by a factor of two and discussing the effect on the slope, which decreases. The presenter also shows how to graph the transformations and update the function’s equation. Next, the video covers vertical stretching by a factor of two, explaining how to multiply the entire function by the stretch factor, and showing both the graphing and notation methods to find the new function equation.
Takeaways
- 🧠 Horizontally stretching a function by a factor of two reduces the slope.
- 🔢 Horizontal stretching affects only the X portion of a function.
- 🔀 You can either divide the X by 2 or multiply it by 1/2 for horizontal stretching.
- 📉 After horizontally stretching, the slope of a line decreases (e.g., from 3 to 3/2).
- 📝 Graphing helps visualize how stretching changes the shape of a function.
- 📈 When stretching horizontally, multiply each X-coordinate by the stretch factor.
- 📊 Vertically stretching by a factor of two increases the slope and makes the function taller.
- ⬆️ Vertically stretching changes the Y-coordinates of the function.
- ✏️ Multiplying the entire function by the stretch factor applies vertical stretching.
- 📐 Using both graphing and notation helps reinforce understanding of function transformation.
Q & A
What is the main focus of the video?
-The video focuses on stretching and compressing functions, specifically discussing how to horizontally and vertically stretch a function and how to write the new equation after these transformations.
What happens when a function is horizontally stretched?
-When a function is horizontally stretched, the slope of the function decreases, making the function appear 'flatter.' The x-values are affected, and this results in the graph stretching outward horizontally.
How do you horizontally stretch a function by a factor of 2?
-To horizontally stretch a function by a factor of 2, you need to divide the x-variable by 2. Alternatively, you can multiply the x-variable by 1/2, as both approaches yield the same effect.
What impact does horizontal stretching have on the slope of the function?
-Horizontal stretching reduces the slope of the function. For example, if the slope is initially 3, it becomes 3/2 after a horizontal stretch by a factor of 2.
What does the notation 'G(x)' represent in the video?
-In the video, 'G(x)' represents the transformed function after applying either a horizontal or vertical stretch to the original function 'f(x).'
How can you visually check if a horizontal stretch was applied correctly?
-You can visually check by graphing both the original function and the transformed function. The transformed function should look stretched horizontally, with the x-coordinates of key points multiplied by the stretching factor.
What is the key difference between horizontal and vertical stretching?
-Horizontal stretching affects the x-values of the function and makes the graph wider, while vertical stretching affects the y-values, making the graph taller or shorter depending on the factor.
How do you vertically stretch a function by a factor of 2?
-To vertically stretch a function by a factor of 2, you multiply the entire function by 2, which scales the y-values by 2 and makes the graph taller.
What happens to the slope when a function is vertically stretched?
-When a function is vertically stretched, the slope increases. For example, if the initial slope is 3, it becomes 6 after a vertical stretch by a factor of 2.
What are two methods mentioned in the video for finding the transformed function?
-The video explains two methods: using notation (mathematically altering the function) and graphing (visually transforming the function by adjusting the coordinates and then plotting the new points).
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)