Bases numéricas y números binarios | Curso de electrónica digital | #1
Summary
TLDREl guion del video explica cómo funciona la numeración en diferentes bases, destacando el sistema decimal que utiliza 10 cifras y se extiende a bases como la binaria (base 2) y hexadecimal (base 16). Se ilustra cómo se realizan operaciones básicas como la suma y la conversión de números de una base a otra, utilizando ejemplos para demostrar cómo se convierte un número de base 10 a binario y viceversa. Además, se menciona que en bases mayores a 10, como la hexadecimal, se utilizan letras para representar valores superiores a 9. El video es una introducción a la numeración y operaciones aritméticas en diferentes bases, preparando al espectador para temas más avanzados en futuras sesiones.
Takeaways
- 😀 Los números binarios son una forma de representar números en el sistema de numeración base 2, utilizando solo los dígitos 0 y 1.
- 🧮 El sistema decimal es el sistema de numeración que utiliza 10 cifras (0-9) y es el más comúnmente utilizado en la vida cotidiana.
- 🔢 En sistemas de numeración diferentes al decimal, como el hexadecimal (base 16), se utilizan letras para representar valores mayores a 9, donde 'A' equivale a 10, 'B' a 11, hasta 'F' que equivale a 15.
- 💡 Para convertir un número de cualquier base a base 10, se multiplica cada dígito por la correspondiente potencia de la base y se suman los resultados.
- 📚 El proceso de conversión de números de una base a otra se explica a través de ejemplos en el guion, como el número 156 en base 10 que se convierte a 234 en base 8.
- 📈 La división es el método clave para convertir de base 10 a cualquier otra base, donde se divide el número entre la base y se toman los residuos para formar el número en la nueva base.
- 🔄 En el caso de bases mayores a 10, se siguen las mismas reglas de multiplicación y suma, pero se incluyen las letras para representar cifras que exceden el valor de 9.
- 💻 Los sistemas digitales y computacionales suelen operar con números binarios debido a la simplicidad de trabajar con 'unos' y 'ceros'.
- 📉 El ejemplo del número 5428 en base 10 se desglosa para mostrar cómo se asignan potencias de 10 a cada cifra y se suman para obtener el valor original.
- 🔢 La representación de números con decimales en diferentes bases sigue un proceso similar, donde las potencias son negativas a partir del punto decimal.
Q & A
¿Qué significa 'unidad 11 bases numéricas y los números, binarios' en el contexto del guion?
-Es el título de la lección que se está explicando, que se centra en las bases numéricas, específicamente en la base binaria, y cómo los números binarios son utilizados en los sistemas de computación.
¿Por qué se considera que la suma de 10 + 11 en binario da como resultado 101?
-En el sistema binario, los números se representan solo con dígitos 0 y 1. La suma de 10 (2 en decimal) más 11 (3 en decimal) da 15, que en binario se escribe como 1110, no 101. El guion podría haber utilizado un ejemplo simplificado para explicar la idea de suma binaria.
¿Qué es el sistema de numeración decimal y cómo se relaciona con el número 5428?
-El sistema de numeración decimal es un sistema de numeración posicional que utiliza 10 dígitos (0 a 9). El número 5428 se forma combinando estos dígitos y asignándoles potencias de 10, donde 5 está en la posición de 10^3, 4 en 10^2, 2 en 10^1 y 8 en 10^0.
¿Cómo se representa un número decimal en el sistema decimal?
-Un número decimal en el sistema decimal se representa asignando potencias negativas de 10 a las cifras que están después del punto decimal, como 10^-1, 10^-2, etc.
¿Cuál es la diferencia entre los sistemas de numeración decimal y binario?
-El sistema decimal utiliza 10 dígitos y es el sistema que usamos comúnmente, mientras que el sistema binario solo utiliza 2 dígitos, 0 y 1, y es el sistema que utilizan los computadores para procesar información.
¿Qué es una base numérica y cómo se relaciona con el ejemplo del número 1111 en binario?
-Una base numérica es el sistema de numeración que utiliza un número fijo de símbolos. En el ejemplo del número 1111 en binario, la base es 2, lo que significa que se usan potencias de 2 para representar el número.
¿Cómo se convierte un número de base 16 (hexadecimal) a base 10?
-Para convertir un número de base 16 a base 10, se multiplica cada dígito por la potencia correspondiente de 16, comenzando desde la derecha (potencia 0) y aumentando la potencia con cada posición a la izquierda. Luego, se suman los productos obtenidos.
¿Qué es la base 8 y cómo se relaciona con el ejemplo del número 156 en base 10?
-La base 8, también conocida como octal, es un sistema de numeración que utiliza 8 dígitos (0 a 7). Para convertir el número 156 de base 10 a base 8, se divide repetidamente el número entre 8, tomando nota de los residuos, hasta que el resultado de la división sea menor que 8.
¿Cómo se determina el número resultante al convertir de base 10 a otra base?
-El número resultante al convertir de base 10 a otra base se determina tomando el resultado de la última división y los residuos de cada una de las divisiones anteriores, de derecha a izquierda.
¿Qué se aprenderá en el siguiente vídeo mencionado en el guion?
-En el siguiente vídeo se aprenderá cómo convertir números con punto decimal de cualquier base a base 10 y realizar operaciones aritméticas básicas en diferentes bases numéricas.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
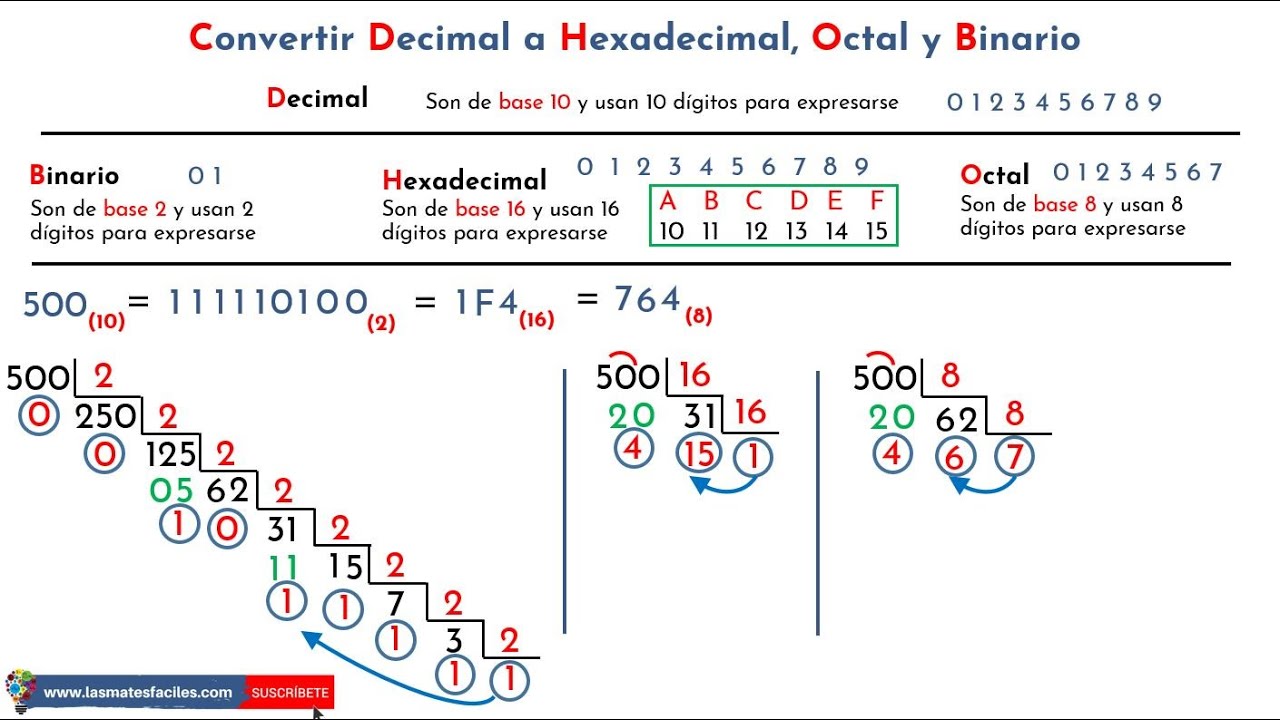
Convertir: Decimal a Binario - Decimal a Hexadecimal - Decimal a Octal - Ejemplos paso a paso!

Sistemas numéricos: Binario, Decimal y Hexadecimal

Sistemas de Numeración
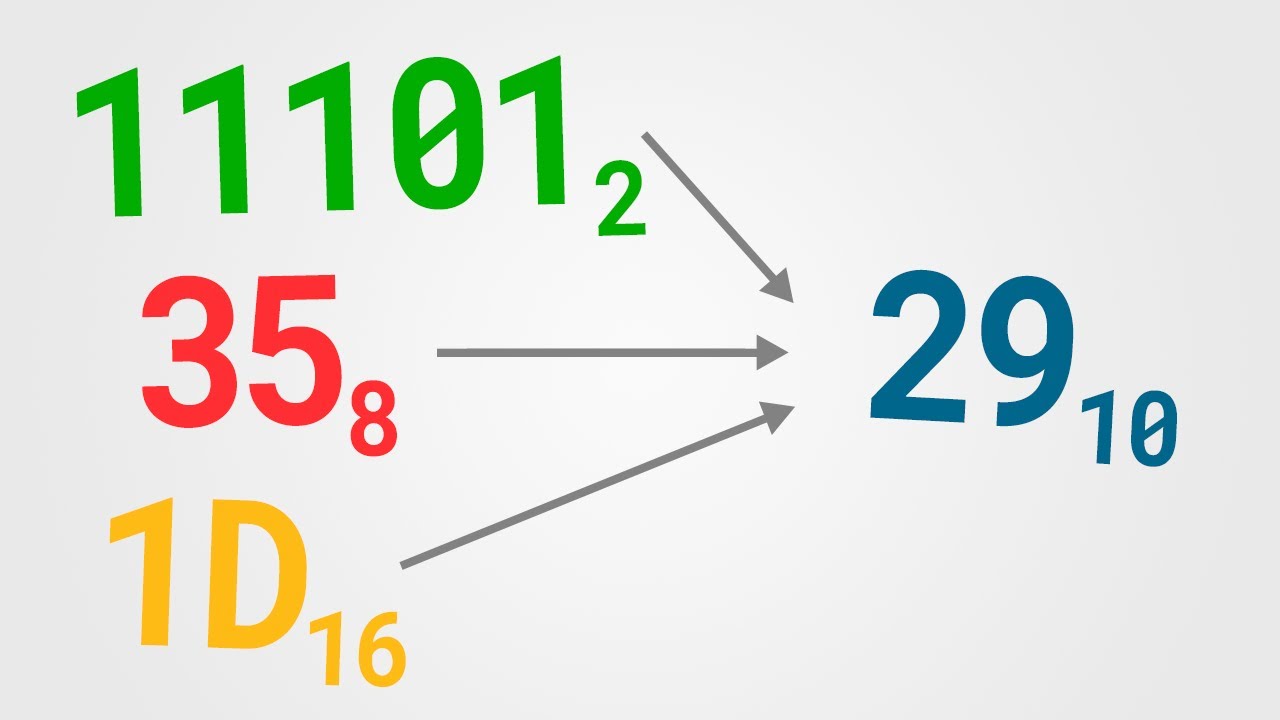
Conversiones entre sistemas de numeración (Binario, octal y hexadecimal a decimal)

Sistemas de Numeración (DECIMAL, BINARIO y HEXADECIMAL) - Explicación y tabla comparativa

The binary code | Explanaiton
5.0 / 5 (0 votes)
