02 Proportionality Theorems
Summary
TLDRIn this educational video, Johnny guides his student Kanya through proving the Proportionality Theorem in geometry. The theorem states that a line parallel to one side of a triangle divides the other two sides proportionally. The lesson involves constructing triangles, calculating areas using the base and height, and setting up ratios to demonstrate the theorem. The video also explores the converse of the theorem, showing how it can be reversed to prove parallelism, and encourages viewers to practice with different triangle configurations.
Takeaways
- 📘 The lesson focuses on the proportionality theorem in mathematics, which is a proven mathematical statement.
- 📐 The theorem states that a line drawn parallel to one side of a triangle divides the other two sides proportionally.
- 🔍 To prove a geometry theorem, one must clearly define what needs to be proved and what information is given.
- 📊 A labeled diagram is essential for visualizing the proof and understanding the relationships between elements.
- 📏 The proof involves constructing perpendicular heights from points where the line intersects the sides of the triangle.
- 📉 The area of a triangle is calculated using the formula: area equals half times base times height.
- 🔢 The proof compares the ratios of the areas of triangles formed by the line and the sides of the original triangle.
- 📌 The proof concludes by showing that the ratios of the areas are equal, thus proving the proportionality theorem.
- 🔄 The lesson also discusses the converse of the theorem, which can be proven by reversing the given and required parts of the original theorem.
- 🌐 Additional practice is suggested by considering different positions of the line relative to the triangle and proving the theorem in those cases.
- 💻 For further learning, the lesson directs students to the website www.mindset.co.za for more resources.
Q & A
What is a theorem in mathematics?
-A theorem in mathematics is a statement or fact that has been proven using accepted mathematical operations and arguments that were previously established.
What is the proportionality theorem in the context of the provided script?
-The proportionality theorem states that a line drawn parallel to one side of a triangle divides the other two sides proportionally.
What is the first step in proving a geometry theorem according to the script?
-The first step in proving a geometry theorem is to decide clearly what it is that must be proved and what information is given.
Why is a labeled diagram important in the proof of a theorem?
-A labeled diagram is important because it helps visualize what the proof is about and ensures that all elements of the proof are clearly identified and understood.
What is the formula for the area of a triangle mentioned in the script?
-The formula for the area of a triangle mentioned in the script is 'area equals half times base times height'.
How does the proof use the area of triangles to establish proportionality?
-The proof uses the area of triangles by constructing perpendicular heights and comparing the ratios of the areas of the triangles to establish the proportionality of the sides of the triangle.
What does the proof demonstrate about the areas of triangles bde and CDE?
-The proof demonstrates that triangles bde and CDE have the same area because they share the same base (de) and lie between the same parallel lines (D and BC), which means they have the same perpendicular height.
What is the converse of the theorem discussed in the script?
-The converse of the theorem discussed is that if a line divides two sides of a triangle proportionally, then it is parallel to the third side of the triangle.
Why is it important to consider different placements of the line in the triangle?
-It is important to consider different placements of the line in the triangle to show the versatility and robustness of the theorem, ensuring that it holds true regardless of the line's position relative to the triangle's sides.
What additional resources are mentioned in the script for further learning?
-The script mentions the advanced ukian geometry task video and the website www.mindset.co.za for further learning on the topic.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Kesebangunan & Kongruensi (5) - Rumus Kesebangunan Trapesium - Matematika SMP
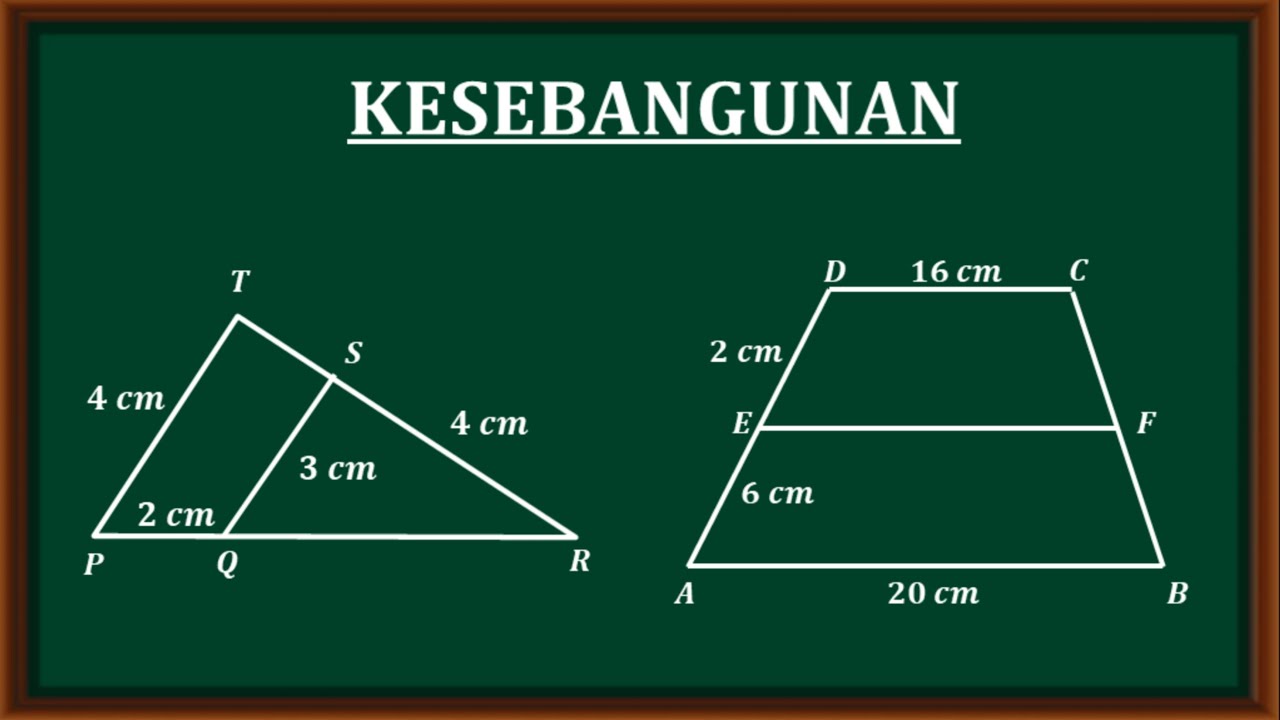
Kesebangunan - soal dan pembahasan materi kesebangunan matematika tingkat SMP kelas ix

Teorema de TALES | Prof. Gis/

Matematika Kelas 9 | Kesebangunan pada Segitiga Siku-siku

O Teorema de Tales

Teorema yang Jarang Diketahui Namanya
5.0 / 5 (0 votes)