Hanya 5 menit anda paham Refleksi terhadap sumbu-𝒙
Summary
TLDRThis educational video script discusses the concept of reflection in the coordinate plane, specifically focusing on reflection across the x-axis or the line y = 0. The script uses examples of triangles and a quadrilateral to illustrate how points are mirrored, with their y-coordinates negated while x-coordinates remain unchanged. The explanation is clear and methodical, providing viewers with a solid understanding of how to determine the reflected points in a Cartesian coordinate system.
Takeaways
- 📏 The lesson discusses the concept of reflection in the coordinate plane, specifically reflection across the x-axis or the line y = 0.
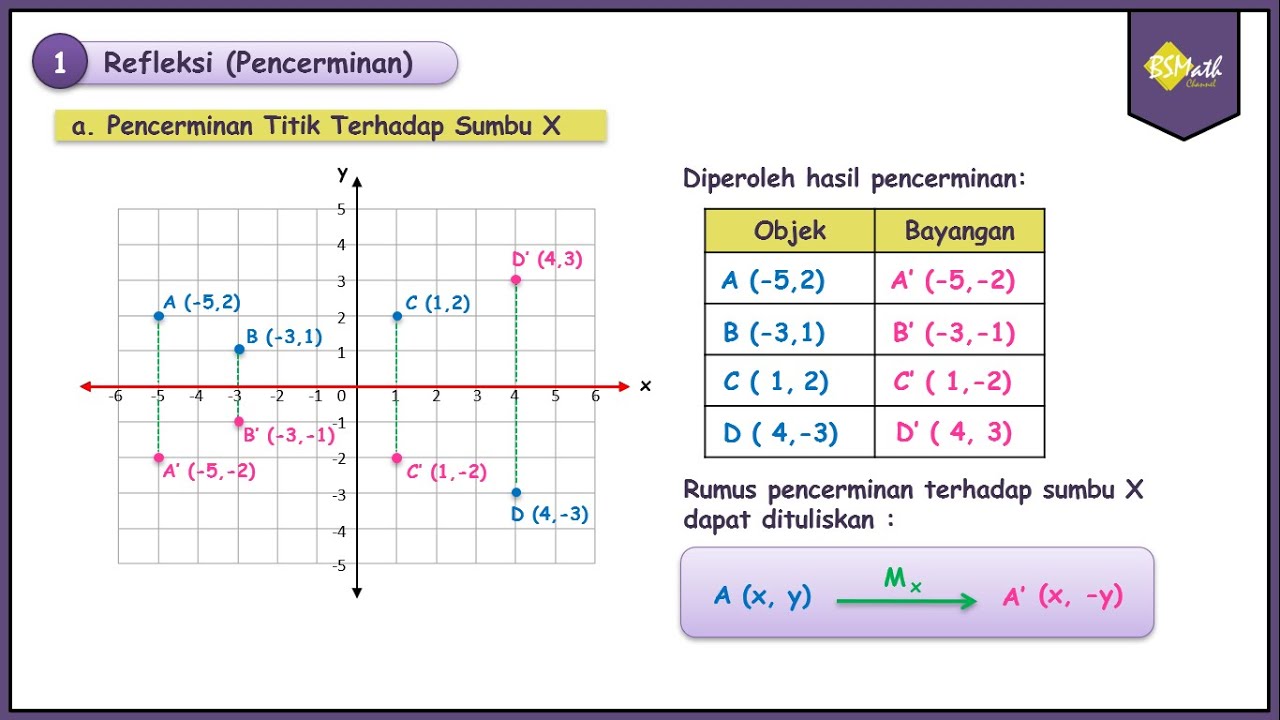
- 🔄 The reflection of a point across the x-axis results in a point that has the same x-coordinate but an opposite y-coordinate.
- 📐 The script provides examples of reflecting points and shapes, such as triangles and a kite, across the x-axis.
- 📈 For a point with coordinates (x, y), its reflection across the x-axis is given by the coordinates (x, -y).
- 📍 The script includes a detailed example of reflecting a triangle ABC with vertices at (-7, 2), (-3, 2), and (-7, 7), resulting in a reflected triangle A'B'C' with vertices at (-7, -2), (-3, -2), and (-7, -7).
- 🪁 The reflection of a kite with points P(1, -3), Q(4, -5), R(9, -3), and S(4, 0) is also discussed, with the reflected points P'(1, 3), Q'(4, 5), R'(9, 3), and S'(4, 0).
- 🔢 The script emphasizes that the y-coordinate changes sign during reflection, while the x-coordinate remains the same.
- 📋 A table is provided to summarize the original points and their reflections, illustrating the rule of changing the y-coordinate to its opposite.
- 🌐 The lesson concludes with a general formula for reflection across the x-axis: if a point P has coordinates (x, y), its reflection P' will have coordinates (x, -y).
- 🙏 The lesson ends with a closing remark in Arabic, wishing peace and blessings upon the viewer.
Q & A
What is the concept of reflection in a coordinate plane?
-Reflection in a coordinate plane refers to the process of creating a mirror image of a point or shape across a line of symmetry, such as the x-axis or the line y = 0.
How do you determine the reflection of a point across the x-axis?
-To find the reflection of a point across the x-axis, you keep the x-coordinate the same and take the opposite of the y-coordinate.
What is the reflection of point A(-7, 2) across the x-axis?
-The reflection of point A(-7, 2) across the x-axis is A'(-7, -2).
What are the coordinates of the reflected point B' when the original point B is (-3, 2)?
-The coordinates of the reflected point B' are (-3, -2).
How does the reflection across the x-axis affect the coordinates of point C(-7, 7)?
-The reflection of point C(-7, 7) across the x-axis results in point C'(-7, -7).
What happens to the y-coordinate of a point when it is reflected across the x-axis?
-When a point is reflected across the x-axis, its y-coordinate changes to its opposite value, while the x-coordinate remains unchanged.
If a point P has coordinates (1, -3), what are its reflected coordinates across the x-axis?
-The reflected coordinates of point P(1, -3) across the x-axis are P'(1, 3).
What is the reflection of a point that lies exactly on the x-axis?
-A point that lies exactly on the x-axis will have the same coordinates after reflection since its y-coordinate is already 0.
Can you provide a general formula for the reflection of a point (x, y) across the x-axis?
-Yes, the reflection of a point (x, y) across the x-axis is given by the point (x, -y).
What is the significance of the reflection process in geometry?
-Reflection is significant in geometry as it helps in understanding symmetry and can be used to transform shapes, solve geometric problems, and analyze mirror images.
How does the reflection across the x-axis relate to the concept of symmetry?
-Reflection across the x-axis is a form of axial symmetry, where a shape can be folded along the x-axis and the two halves will coincide perfectly.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

matematika kelas 9 | Transformasi - Refleksi atau pencerminan terhadap sumbu X
Transformasi Refleksi, Pencerminan Titik Terhadap Sumbu X - Matematika Tingkat Lanjut Kelas XI

Transformasi Geometri Bagian 2 - Refleksi (Pencerminan) Matematika Wajib Kelas 11

TRANSFORMASI GEOMETRI || Matematika Kelas XI SMA

Pencerminan/Refleksi 1| Transformasi Geometri

matematika kelas 9 | Refleksi/Pencerminan terhadap sumbu-Y
5.0 / 5 (0 votes)