Unit 1 Lesson 2 Practice Problems IM® Algebra 2TM authored by Illustrative Mathematics®
Summary
TLDRThe video script is an educational tutorial on geometric sequences, growth factors, and patterns in sequences. It explains how to find subsequent terms in a geometric sequence by multiplying by a constant growth factor. It also demonstrates calculating growth factors by dividing successive terms and applies this concept to a credit card debt example with compounding monthly interest. The script further explores the Sierpinski triangle, illustrating the pattern of shaded triangles and the relationship between the number of triangles and their area over iterations. Additionally, it discusses graphing these patterns and creating custom sequences based on given rules, offering insights into mathematical sequences and their applications.
Takeaways
- 🔢 In a geometric sequence, each term is found by multiplying the previous term by a constant factor, known as the growth factor.
- 📈 The growth factor can be determined by dividing a term by its preceding term in the sequence.
- 💳 A credit card balance with a 2% monthly interest rate increases by 102% of the previous month's balance, calculated by multiplying the balance by 1.02 each month.
- 📊 The number of shaded triangles in a Sierpinski triangle increases exponentially with each step, while the area of each triangle decreases.
- 📉 The graphs of the number of shaded triangles and the area of each triangle in a Sierpinski triangle demonstrate different growth patterns; the number of triangles increases while the area per triangle decreases.
- 🔑 The rule 'four less than three times the previous number' is used to generate sequences where each term is calculated by multiplying the previous term by three and then subtracting four.
- 📐 The Sierpinski triangle is constructed by recursively removing the middle triangle from a set of four congruent triangles, creating a fractal pattern.
- 📘 The area of each triangle in the Sierpinski triangle sequence is calculated by dividing the total area by the number of triangles at each step.
- 💡 The script demonstrates how to apply geometric sequence concepts to real-world scenarios, such as calculating compound interest on a credit card.
- 📌 The script illustrates the process of creating and analyzing sequences using different rules, showcasing the versatility of geometric sequences.
Q & A
What is the definition of a geometric sequence?
-A geometric sequence is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio.
How do you find the next three terms of a geometric sequence if the first two terms are given?
-To find the next three terms of a geometric sequence, you multiply each term by the common ratio to get the subsequent term. For example, if the first term is 1 and the second term is 4, and the common ratio is 2 (since 1*2=2 and 2*2=4), the next three terms would be 4*2=8, 8*2=16, and 16*2=32.
What is the growth factor of a geometric sequence and how do you calculate it?
-The growth factor, also known as the common ratio, is the number by which you multiply to get from one term in a geometric sequence to the next. It can be calculated by dividing any term by its preceding term.
How does the growth factor affect the terms in a geometric sequence?
-The growth factor determines the rate at which the terms in a geometric sequence increase or decrease. A growth factor greater than 1 will increase the terms, while a growth factor less than 1 will decrease them.
If a credit card balance of $1000 has a 2% monthly interest rate and no payments are made, how does the balance change over time?
-With a 2% monthly interest rate, the balance increases by 2% each month. This means the balance is multiplied by 1.02 each month. For example, after one month, the balance would be $1000 * 1.02 = $1020.
What is the pattern of shaded triangles in the Sierpinski Triangle, and how does it relate to the number of steps taken?
-In the Sierpinski Triangle, at each step, the number of shaded triangles increases by a factor of three, and the area of each triangle is divided by four. This pattern continues with each iteration.
How can you graph the number of shaded triangles and the area of each triangle in the Sierpinski Triangle as a function of the step number?
-You can graph the number of shaded triangles by plotting the count on the y-axis against the step number on the x-axis, showing an exponential increase. For the area of each triangle, plot the area on the y-axis against the step number, showing an exponential decrease.
What is the rule for creating a sequence where each number is four less than three times the previous number?
-To create a sequence where each number is four less than three times the previous number, you multiply the previous number by three and then subtract four to get the next number in the sequence.
How does changing the starting number in a sequence affect the subsequent terms when the rule is 'four less than three times the previous number'?
-Changing the starting number in the sequence will result in a different set of numbers following the same rule. Each subsequent term will still be calculated by multiplying the previous term by three and subtracting four, but the values will be different based on the initial number.
Can you provide an example of a different rule for generating a sequence, and what would the next three terms be if starting with 1?
-An example of a different rule could be 'multiply by -1'. Starting with 1, the next three terms would be: 1 * -1 = -1, -1 * -1 = 1, and 1 * -1 = -1.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
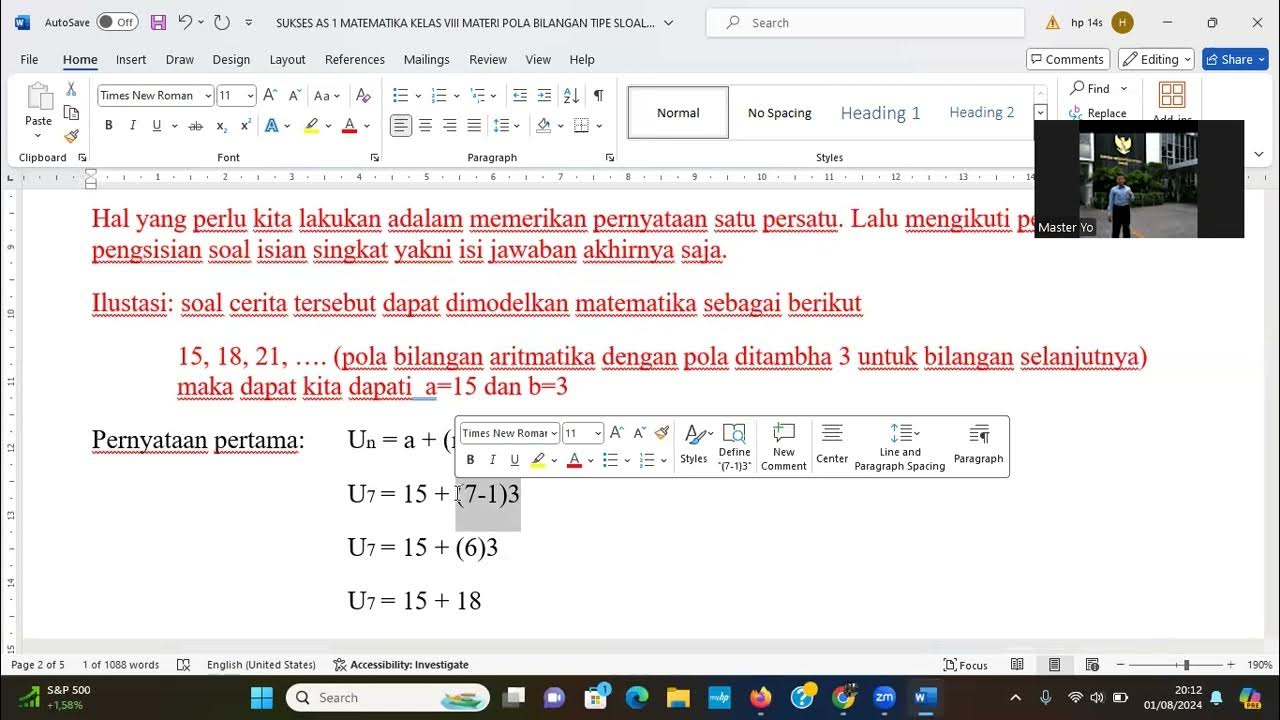
Latihan Soal Pola Bilangan

MATH 10 : DIFFERENTIATING GEOMETRIC SEQUENCE FROM AN ARITHMETIC SEQUENCE (Taglish)

Arithmetic Sequences and Arithmetic Series - Basic Introduction

Grade 10 Math Q1 Ep6: Geometric Sequence VS Arithmetic Sequence

Pre-Calculus - Introduction to Sequence

Arithmetic and Geometric Sequences
5.0 / 5 (0 votes)