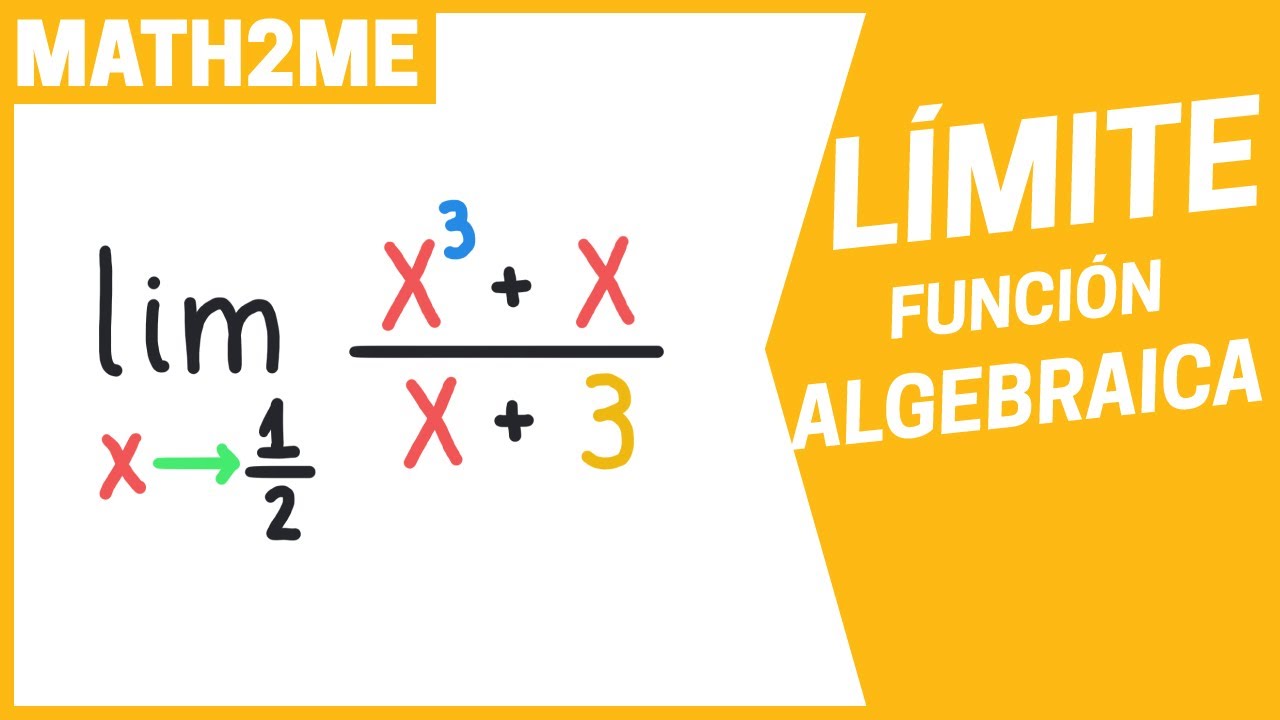
Acercamiento al concepto de límite de una función.

TEBAEV VIDEOS EDUCATIVOS

3 May 202407:47

Summary

TLDREl guion del video explica cómo los límites de funciones son cruciales para entender la continuidad o discontinuidad en matemáticas. Se utiliza la metáfora de un puente que une caminos, destacando la importancia de anticipar y verificar su estado antes de cruzar. Se exploran conceptos como el dominio y el rango, y cómo simplificar fracciones para encontrar límites, como en el caso de una parábola con una discontinuidad en x=2. Además, se menciona que los límites pueden existir sin una imagen correspondiente y viceversa, subrayando la diferencia entre la imagen y el límite en funciones de derecha e izquierda. El video termina con una llamada a la importancia de estos conceptos en el estudio de la matemática en el bachillerato.

Takeaways

🌉 Los puentes son uniones entre caminos que de otro modo estarían separados.
🛠️ Es importante verificar la operatividad de un puente antes de cruzarlo, para anticipar posibles problemas.
📊 Los límites de funciones son usados para establecer puntos de continuidad o falta de ella en las funciones.
🔍 Se pueden determinar singularidades en las funciones visualizando el comportamiento cerca de un punto de interés.
📉 En el caso de una parábola con discontinuidad en el número 2, no se puede dividir entre cero, por lo que 2 no está en el dominio.
👀 El aproximación a un punto de discontinuidad muestra cómo la función se comporta cerca de ese punto, aunque el punto en sí mismo no esté en el dominio.
🔄 La eliminación algebraica de un factor común en el numerador y denominador puede simplificar la representación de una función.
📐 La representación de una función continua como un polinomio cuadrático es válida siempre y cuando se conserve el dominio original.
👉 Las funciones de la izquierda y de la derecha pueden tener el mismo dominio, pero uno puede incluir un punto específico que el otro no.
📈 El cálculo del límite en un polinomio se puede hacer por simple sustitución, ya que la imagen y el límite son numéricamente iguales.
🔄 El proceso de determinación del límite puede incluir el cálculo de la imagen, pero la imagen en sí misma no es el límite.
🔍 La expresión '0 sobre 0' indica que un factor común en el numerador y denominador puede ser simplificado antes de calcular el límite.

Q & A

¿Qué representan los puentes en el contexto del guión?
-En el guión, los puentes son una metáfora para las uniones entre caminos que de otro modo estarían separados, y su importancia para cruzar antes de enfrentar desafíos.
¿Qué son los límites de funciones y por qué son importantes?
-Los límites de funciones son una herramienta matemática que nos permite determinar el comportamiento de una función cerca de un punto, incluso si la función no está definida en ese punto, y son importantes para entender la continuidad y la convergencia de la función.
¿Cómo se determina si un punto es de discontinuidad en una función?
-Se determina la discontinuidad al observar si hay un 'salto' o una interrupción en la función, como en el caso de una parábola con una discontinuidad en el número dos, donde no se puede dividir entre cero.
¿Qué es el dominio de una función y por qué es relevante?
-El dominio de una función es el conjunto de todos los valores de x para los cuales la función está definida. Es relevante porque define los puntos a los que la función puede tomar valores y es crucial para entender las limitaciones de la función.
¿Qué sucede cuando un valor no pertenece al dominio de una función?
-Cuando un valor no pertenece al dominio de una función, significa que la función no está definida en ese punto, y por lo tanto, no puede tomar un valor en ese punto específico.
¿Cómo se simplifica una función que contiene un término común en el numerador y denominador?
-Se simplifica realizando una división algebraica, eliminando el término común, lo que da lugar a una expresión más simple, como un polinomio de menor grado.
¿Por qué es importante conservar el dominio original al simplificar una función?
-Es importante conservar el dominio original para asegurarse de que la función simplificada tenga el mismo conjunto de valores posibles para x que la función original, evitando la pérdida de información crucial sobre las limitaciones de la función.
¿Cómo se calcula el límite de una función cuando x tiende a un valor específico?
-El límite se calcula sustituyendo el valor específico en la función, o bien aproximando el valor a través de imágenes de puntos cercanos al mismo, siempre y cuando el dominio permita tal aproximación.
¿Qué indica un cero en el denominador al calcular el límite de una función?
-Un cero en el denominador indica una indeterminación en la expresión, lo que sugiere que puede ser necesario simplificar la función o utilizar técnicas como la división de factores comunes para resolver la indeterminación.
¿Por qué la imagen de un punto puede existir sin que el límite también exista?
-La imagen de un punto es el valor que toma la función en ese punto, mientras que el límite describe el comportamiento de la función cerca de ese punto. Es posible que la función tenga un valor en un punto específico, pero que su comportamiento cerca de ese punto no sea definido o convergente, por lo que el límite no existe.
¿Cómo se relaciona el concepto de límite con la idea de aproximación en el guión?
-El concepto de límite se relaciona con la aproximación en el sentido de que el límite describe cómo la función se acerca a un valor específico a medida que x se acerca a un punto, sin necesariamente alcanzar ese punto, similar a cómo se aproxima a un puente para determinar si está intacto o destruido.

Outlines

00:00

🌉 Funciones y Límites: Unión y Ruptura

El primer párrafo compara los puentes con uniones entre caminos que podrían estar separados. Introduce el concepto de límites de funciones como una herramienta para anticipar y determinar singularidades en las funciones, como puntos de discontinuidad. Se ejemplifica con una parábola que tiene una discontinuidad en el número dos, mostrando que a pesar de que el número dos no pertenece al dominio, se puede aproximar el comportamiento de la función en ese punto, donde el límite es cero. También se menciona la importancia de mantener el dominio original de la función y cómo las funciones de la izquierda y la derecha pueden tener el mismo comportamiento a pesar de que uno incluye el punto de discontinuidad y el otro no.

05:02

📚 Límites y Polinomios: Simplificación y Cálculo

El segundo párrafo se enfoca en el cálculo de límites para funciones polinómicas, donde la imagen y el límite suelen coincidir. Se explica que en estos casos, la sustitución directa de 'x' en la ecuación da el mismo resultado que el límite. Sin embargo, cuando hay una indeterminación de la forma '0/0', se puede simplificar primero el término antes de calcular el límite. Se resalta que el límite no es la imagen misma, sino una aproximación que nos permite entender el comportamiento de la función cerca de un punto de interés. Finalmente, se vuelve a la metáfora del puente, donde la imagen es el puente y el límite es la investigación de su estado a través de la aproximación.

Mindmap

Keywords

💡Puentes

Los puentes son estructuras que unen dos caminos que de otro modo estarían separados. En el contexto del video, se utiliza la metáfora de los puentes para representar la idea de unir conceptos matemáticos. Por ejemplo, el puente simboliza la conexión entre diferentes puntos de una función matemática y su continuidad.

💡Límites de funciones

Los límites de funciones son un concepto fundamental en el análisis matemático que describe el comportamiento de una función cuando el valor de la variable tiende a un límite específico. En el video, se discute cómo los límites son importantes para determinar la continuidad de una función y cómo se pueden visualizar a través de la aproximación de puntos cercanos.

💡Continuidad

La continuidad es una propiedad de una función que indica que la función no tiene interrupciones ni 'saltos' en un punto dado. En el script, se menciona la importancia de determinar los puntos de continuidad o falta de ella en las funciones, que es crucial para entender el comportamiento de la función en esos puntos.

💡Dominio

El dominio de una función es el conjunto de todos los valores posibles que puede tomar la variable independiente. En el video, se destaca que el dominio es parte fundamental de la definición de una función y que puede influir en la existencia de límites y continuidad.

💡Simplificación algebraica

La simplificación algebraica es el proceso de reducir una expresión matemática a su forma más simple, a menudo eliminando factores comunes. En el script, se utiliza la simplificación para transformar una fracción en un polinomio cuadrático, lo cual es importante para entender la continuidad de la función.

💡Funciones continuas

Una función continua es aquella que no tiene interrupciones y su gráfico no tiene 'saltos' o 'cortes'. En el video, se menciona que las funciones continuas son representadas por una misma ecuación, pero pueden tener dominios diferentes.

💡Polinomio cuadrático

Un polinomio cuadrático es una expresión matemática que involucra un término de grado dos más otros términos de grado menor. En el script, se simplifica una fracción a un polinomio cuadrático, lo que permite analizar la continuidad de la función sin el problema de divisiones por cero.

💡Cálculo de límites

El cálculo de límites es el proceso de encontrar el valor que toma una función cuando la variable tiende a un punto específico. En el video, se muestra cómo calcular límites en diferentes situaciones, incluyendo el uso de la sustitución directa y la división de factores comunes.

💡Binomio

Un binomio es una suma o resta de dos términos. En el script, se menciona el binomio 'x - 1' como un factor común en el numerador y denominador, lo que permite la simplificación y el cálculo de límites en casos de divisiones por cero.

💡Imágenes y límites

En el contexto matemático, la 'imagen' se refiere al valor que toma una función para un valor dado de la variable, mientras que el 'límite' es el comportamiento de la función cerca de un punto. En el video, se contrasta la imagen con el límite, destacando que pueden ser iguales, distintos o no existir.

Highlights

Los puentes son uniones de caminos que de otra forma quedarían separados.

La importancia de anticipar y verificar la operatividad de un puente antes de cruzarlo.

Los límites de funciones establecen puntos de continuidad o falta de ella en las funciones.

La visualización de puntos cercanos al de interés para determinar singularidades en funciones.

Ejemplo de una parábola con discontinuidad en el número dos, evidenciando la no pertinencia al dominio.

La aproximación a cero en el denominador que impide la división y la existencia de un punto en el dominio.

La naturaleza del límite como aproximación a valores que pueden o no pertenecer al dominio.

La representación del límite de una función y su forma de expresarlo.

La eliminación algebraica del factor común en el numerador y denominador de una función.

La representación de una función continua a través de un polinomio cuadrático.

La conservación del dominio original tras simplificación algebraica de una función.

La diferencia entre el conjunto de funciones de la izquierda y la derecha, y su representación por la misma ecuación.

El cálculo de límites en polinomios a través de sustitución simple.

La coincidencia numérica entre la imagen y el límite en el caso de polinomios.

El caso de cero sobre cero, indicativo de que el binomio es factor de numerador y denominador.

El proceso de determinación de límites que puede incluir el cálculo de la imagen pero no es la imagen en sí.

La posibilidad de que la imagen y el límite existan y sean distintos o no existir ninguno.

La alegoría del puente en el camino para entender la aproximación y la investigación del límite.