LÍMITE de una función algebraica - ejercicio
Summary
TLDREl guion de este video explica cómo calcular límites de funciones algebraicas. Se muestra cómo sustituir valores en expresiones para encontrar límites y se ejemplifica con funciones como x+1 y x^2 + 3x + 1. Se discute la indeterminación en límites de funciones racionales y se resuelve un ejemplo paso a paso usando el método de mariposa para fracciones. Además, se enfatiza la importancia de conocer las discontinuidades en las gráficas para entender mejor los límites.
Takeaways
- 📐 Para resolver el límite de una función algebraica, se sustituye el valor de x por el límite al cual tiende.
- 📈 Al graficar la función x, se obtiene una línea recta de 45 grados que pasa por el origen.
- ➕ Al agregarle un +1 a la función x, se traslada verticalmente hacia arriba.
- 🔍 Al evaluar el límite de una función algebraica, se busca el resultado cuando x se acerca a un valor específico.
- 🔢 En el ejemplo dado, al sustituir x por -4 en la función \(x^2 + 3x + 1\), se obtiene un resultado de +17.
- 📉 La gráfica de una función cuadrática con signo positivo en la variable al cuadrado indica una parábola con concavidad positiva.
- 🔄 Para resolver límites de funciones racionales, se intenta sustituir y simplificar hasta obtener un valor numérico o identificar una indeterminación.
- 🔄 Al dividir fracciones con diferentes denominadores, se utiliza el método de mariposa para encontrar un denominador común y simplificar.
- 📉 Al graficar una función racional, se verifica que el límite se acerca a un valor específico cuando x se acerca a un punto dado.
- ⚠️ Es importante tener en cuenta las indeterminaciones y discontinuidades en la gráfica de una función para entender correctamente sus límites.
Q & A
¿Qué significa 'resolver el límite de una función'?
-Resolver el límite de una función significa determinar el valor que toma la función cuando la variable independiente se acerca a un punto específico, ya sea desde la izquierda, la derecha o ambos lados.
¿Cómo se evalúa el límite de una función algebraica cuando x tiende a un valor específico?
-Para evaluar el límite de una función algebraica, se sustituye el valor específico de x en la expresión algebraica y se simplifica la expresión para obtener el resultado numérico.
¿Qué representa una función que es una línea recta de 45 grados que pasa por el origen?
-Una función que es una línea recta de 45 grados que pasa por el origen representa una relación directa entre x e y, donde el cambio en x se refleja igualmente en y, y su ecuación matemática es de la forma y = x.
¿Cómo se interpreta el resultado del límite cuando se añade un +1 a una función que ya es una línea recta de 45 grados?
-Añadir un +1 a una función que es una línea recta de 45 grados significa que la gráfica se traslada verticalmente hacia arriba en una unidad, lo que cambia el límite de la función en 1 unidad más que el valor original.
¿Qué método se usa para evaluar el límite de una función algebraica cuando x tiende a menos 4?
-Para evaluar el límite cuando x tiende a menos 4, se sustituye x por -4 en la expresión algebraica y se simplifica para obtener el resultado numérico.
¿Cómo se determina si un límite resulta en una indeterminación?
-Un límite resulta en una indeterminación cuando la simplificación de la expresión algebraica conduce a una forma como 0/0 o infinito/infinito, lo que no se puede calcular directamente.
¿Qué significa 'desarrollar las operaciones' al evaluar un límite?
-Desarrollar las operaciones al evaluar un límite significa expandir y simplificar la expresión algebraica sustituyendo los valores donde corresponde para ver si se puede obtener un resultado numérico claro.
¿Cuál es la importancia de conocer el vértice de una parábola al evaluar su límite?
-El vértice de una parábola indica el punto de mínimo o máximo de la función, y al conocerlo, se puede entender cómo se comporta la función y sus límites cerca de ese punto.
¿Cómo se evalúa el límite de una función racional cuando x tiende a un valor que hace que el denominador sea cero?
-Cuando x tiende a un valor que hace que el denominador sea cero en una función racional, se puede obtener una indeterminación. Para resolverlo, se deben simplificar las fracciones y, si es posible, se evalúa el límite utilizando factorización o el método de mariposa.
¿Qué es el método de mariposa y cómo se usa para resolver fracciones con denominadores diferentes?
-El método de mariposa es una técnica para sumar o restar fracciones con denominadores diferentes, consistiendo en encontrar un denominador común y luego cambiar los numeradores de acuerdo con el nuevo denominador para poder realizar la operación.
¿Por qué es importante conocer la existencia de la función y sus discontinuidades al evaluar límites?
-Es importante conocer la existencia de la función y sus discontinuidades al evaluar límites para entender en qué intervalos la función es definida y si hay valores específicos que podrían causar problemas al calcular límites, como divisiones por cero.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

PROPIEDADES DE LOS LÍMITES CON EJEMPLOS (Para principiantes)
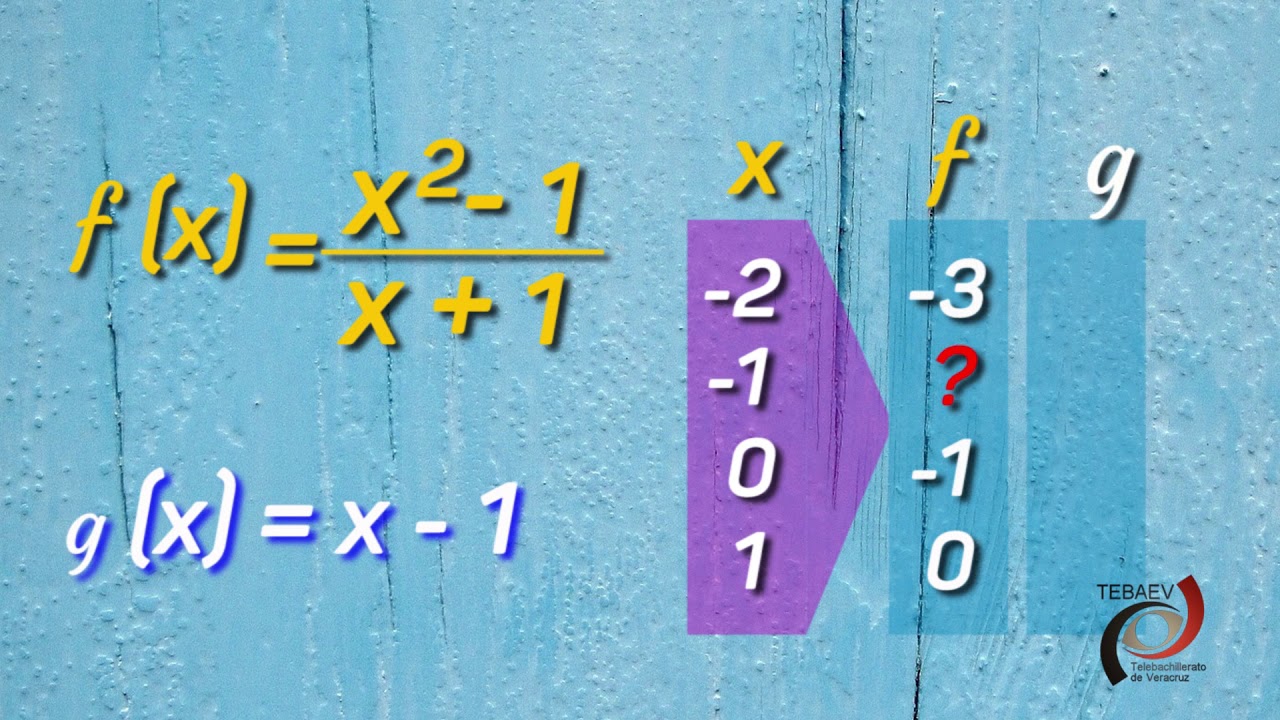
Concepto e interpretación de límites.

¿Qué es la derivada? ¿De donde sale?

✅LÍMITES por FACTORIZACIÓN | 𝙉𝙤 𝙢á𝙨 𝙍𝙚𝙥𝙧𝙤𝙗𝙖𝙧😎🫵💯 | Cálculo Diferencial

⛔️ Cómo calcular LIMITES LATERALES FUNCIÓN POR PARTES - FUNCIÓN A TROZOS| Juliana la profe
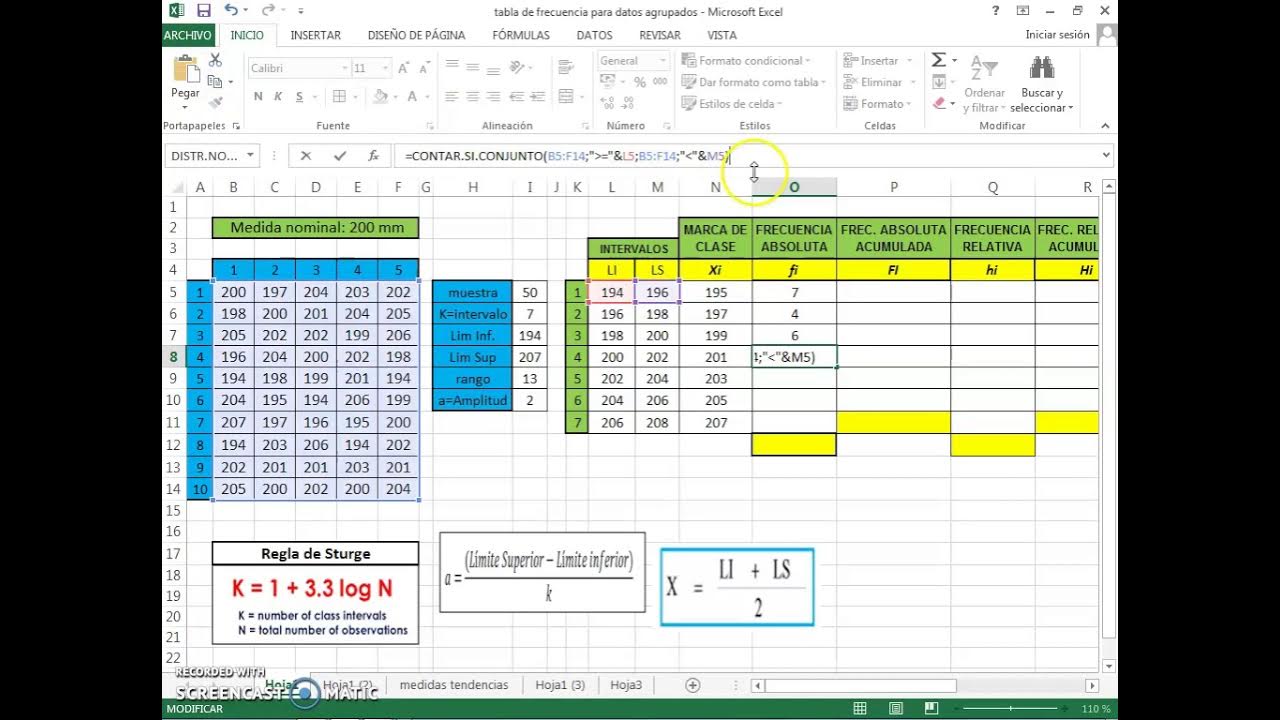
Tabla de Frecuencia para datos agrupados en intervalos con Excel - "DESCARGA EL ARCHIVO"
5.0 / 5 (0 votes)
