Derivada de un producto | Ejemplo 2 consejo
Summary
TLDRIn this tutorial, the instructor explains how to approach the derivative of a product of two binomials. They recommend multiplying the binomials first, then differentiating, instead of directly applying the product rule, which can simplify the process. The instructor walks through the steps of multiplying the terms and simplifies the expression before performing the derivative. Examples are provided to illustrate the method, and the video concludes with an exercise for the viewers to practice, offering a clear and efficient approach to solving these types of problems.
Takeaways
- 😀 The video is part of a course on derivatives, focusing on the derivative of a product of two functions.
- 😀 The instructor advises not to directly apply the product rule but to first multiply the terms before differentiating.
- 😀 When faced with products of two binomials without exponents outside the parentheses, the recommended approach is to multiply first and then differentiate.
- 😀 The multiplication process involves multiplying the first term by both terms of the second binomial and repeating this for all combinations.
- 😀 After multiplying, terms with similar powers of 'x' are combined to simplify the expression before differentiating.
- 😀 The derivative is then taken from the simplified polynomial expression, which results in a much easier calculation.
- 😀 The instructor illustrates with an example of multiplying two binomials and then taking the derivative of the resulting polynomial.
- 😀 The product of the first and second terms results in terms like x^6, x^4, and x^2 after combining like terms.
- 😀 The derivative process is explained step by step, with the instructor showing how each term is differentiated according to the power rule.
- 😀 At the end of the video, viewers are encouraged to practice by solving a similar exercise and to check the solution provided in the video.
Q & A
What is the main topic of the video?
-The main topic of the video is the derivative of a product, specifically how to differentiate products of binomials.
What advice does the presenter give about differentiating products?
-The presenter advises that when dealing with products of binomials, it is often better to multiply the binomials first before differentiating, instead of directly applying the product rule for derivatives.
Why does the presenter suggest multiplying first before differentiating?
-The presenter suggests multiplying first because it simplifies the expression and makes the differentiation process easier, as seen in the example.
What example does the presenter use to demonstrate this concept?
-The presenter uses an example of the derivative of a product of two binomials, specifically involving terms like 2x³ and x³, and their multiplication and simplification before differentiation.
What are the steps for multiplying the two binomials in the example?
-The first step is to multiply each term of the first binomial by each term of the second binomial, following the distributive property. After multiplying, similar terms are combined.
What is the simplified expression after multiplying the binomials?
-The simplified expression after multiplying the binomials is: 2x⁶ + 10x⁴ - 3x⁴ - 15x², which further simplifies to 2x⁶ + 7x⁴ - 15x².
How is the derivative calculated from the simplified expression?
-The derivative is calculated by applying the power rule to each term. The derivative of 2x⁶ is 12x⁵, the derivative of 7x⁴ is 28x³, and the derivative of -15x² is -30x.
How does the process differ when applying the product rule directly?
-When applying the product rule directly, each term is differentiated separately using the product rule formula, which can involve more complex steps compared to multiplying the binomials first.
What is the purpose of the additional exercise provided in the video?
-The additional exercise is provided for viewers to practice applying the advice given in the video, where they should multiply the binomials first before differentiating.
What is the result of the additional exercise?
-The result of the additional exercise after following the multiplication-first approach is the derivative 36x⁵ - 45x⁴ - 24x³.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Lec 33 - Algebra of polynomials: Multiplication
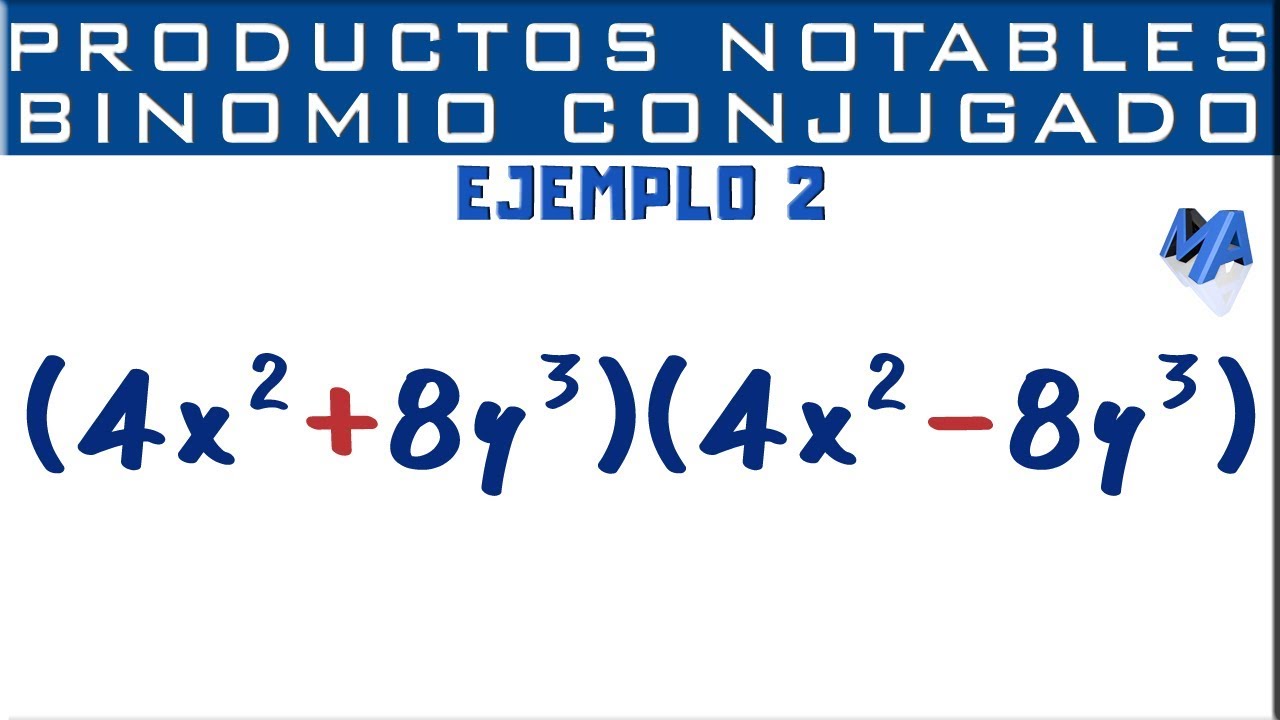
Productos Notables | Binomio Conjugado | Suma por diferencia | Ejemplo 2

AP Precalculus – 4.2 Parametric Functions Modeling Planar Motion

PERKALIAN VEKTOR || Perkalian Dot Product dan Perkalian Cross Product

Problemas de optimización de funciones – Maximizar el producto de los cuadrados de dos números

Cara mudah menentukan nilai maksimum dan minimum suatu fungsi
5.0 / 5 (0 votes)