CIRCLES || PRE-CALCULUS
Summary
TLDRThis video lesson offers an in-depth exploration of circles, beginning with an overview of conic sections and their formation. It defines a circle as the set of points equidistant from a central point, known as the center, and introduces the concept of the radius. The lesson then delves into the standard form of a circle's equation, providing several examples to illustrate how to derive the equation from a given center and radius. The examples cover a range of scenarios, including circles centered at the origin and those with non-integer radii, concluding with a reminder to like, subscribe, and stay tuned for more educational content.
Takeaways
- 📚 The lesson is about the concept of circles within the broader topic of conic sections.
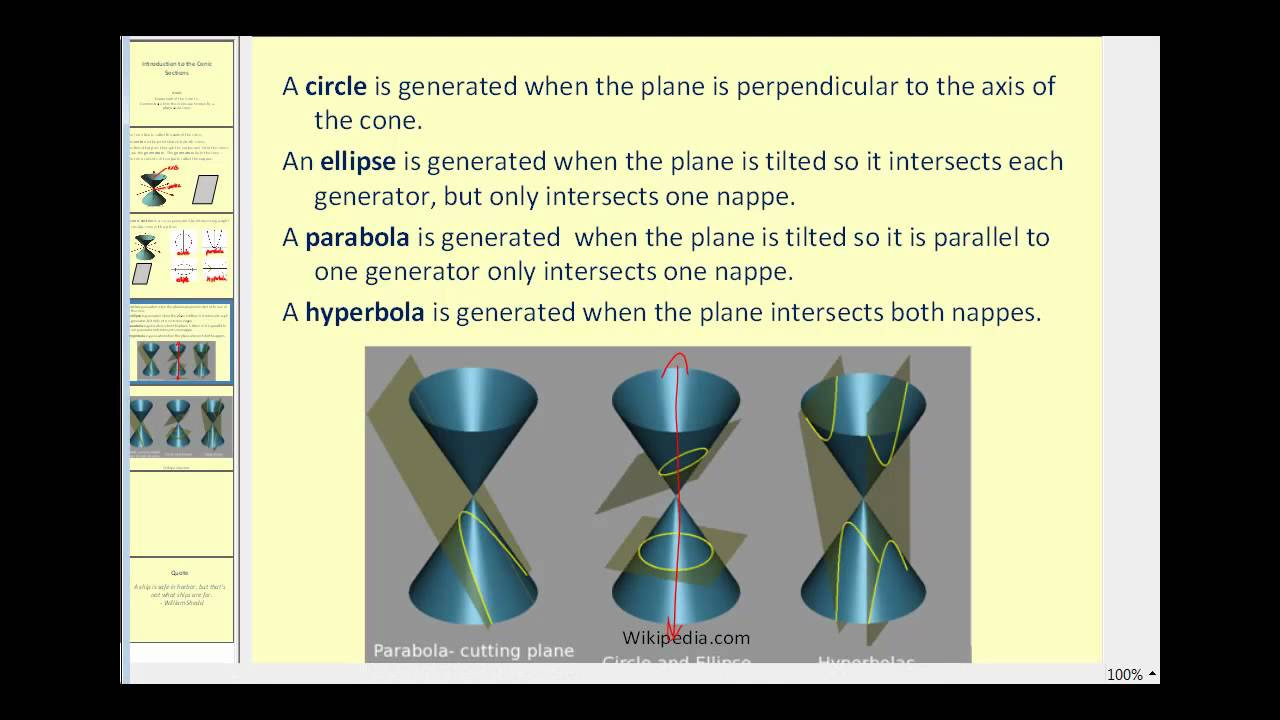
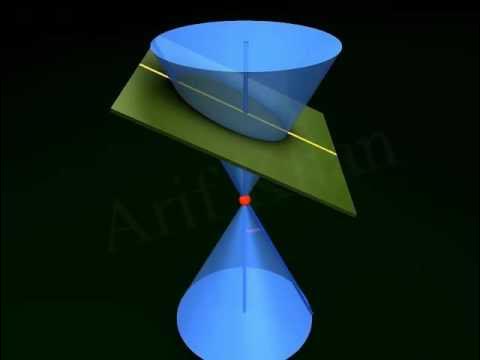
- 📐 Conic sections are formed by the intersection of a plane and a cone at different angles, resulting in four types of conic sections.
- ⭕ A circle is defined as a set of points equidistant from a fixed point, known as the center.
- 📏 The constant distance from the center to any point on the circle is the radius.
- 🔢 The standard form of a circle's equation is \( (x-h)^2 + (y-k)^2 = r^2 \), where \( (h, k) \) is the center and \( r \) is the radius.
- 📈 The video demonstrates how to find the equation of a circle given the center and radius, using the standard form.
- 📝 Examples are provided to illustrate the process of writing the equation of a circle with various centers and radii.
- 🔍 The script includes examples with centers at the origin, as well as with non-zero coordinates, and varying radii.
- 🧩 The importance of understanding the relationship between the center coordinates, radius, and the equation of a circle is emphasized.
- 📉 The video covers cases where the radius is given as a whole number, as well as when it is expressed as a square root.
- 💡 The lesson concludes with a reminder to like, subscribe, and hit the bell for more educational content.
Q & A
What is a conic section?
-A conic section is the intersection of a plane and a cone, which can produce four different types of conic sections depending on the angle at which the plane slices the cone.
What are the four types of conic sections?
-The script does not specify the four types of conic sections, but they are typically a circle, ellipse, parabola, and hyperbola.
What is the definition of a circle in the context of this script?
-A circle is defined as the set of all points on a plane equidistant from a fixed point, known as the center.
What is the standard form of the equation of a circle?
-The standard form of the equation of a circle is (x - h)² + (y - k)² = r², where (h, k) is the center of the circle and r is the radius.
How do you find the equation of a circle with a center at the origin and a radius of 5 units?
-The equation of a circle with a center at the origin (0, 0) and a radius of 5 units is x² + y² = 25.
What is the equation of a circle centered at (0, 3) with a radius of 6 units?
-The equation of a circle centered at (0, 3) with a radius of 6 units is x² + (y - 3)² = 36.
If the center of a circle is at (2, -5) and the radius is 10, what is the equation of the circle?
-The equation of a circle with a center at (2, -5) and a radius of 10 is (x - 2)² + (y + 5)² = 100.
What is the equation of a circle with a center at (1, 5) and a radius of √17 units?
-The equation of a circle with a center at (1, 5) and a radius of √17 units is (x - 1)² + (y - 5)² = 17.
How do you find the equation of a circle with a center at (0, 0) and a radius of 8 units?
-The equation of a circle with a center at the origin and a radius of 8 units is x² + y² = 64.
What is the equation of a circle with a center at (-7, 5) and a radius of 2√14 units?
-The equation of a circle with a center at (-7, 5) and a radius of 2√14 units is (x + 7)² + (y - 5)² = (2√14)².
What is the process to write the equation of a circle given its center and radius?
-To write the equation of a circle given its center (h, k) and radius r, you use the formula (x - h)² + (y - k)² = r², substituting the actual values of h, k, and r.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тариф5.0 / 5 (0 votes)