Fibonacci Sequence and Golden Ratio || Mathematics in the Modern World
Summary
TLDRIn this video, Ram explores the fascinating presence of mathematics in nature, specifically the Fibonacci sequence, which is often found in the arrangement of petals and the growth patterns of various natural phenomena. The script delves into the historical roots of the sequence, its mathematical properties, and its prevalence in art, architecture, and even human biology. The golden ratio, derived from the Fibonacci sequence, is highlighted for its aesthetic appeal and its use in creating harmonious proportions in diverse fields, from Renaissance art to modern-day photography apps. The video also touches on the practical applications of these mathematical concepts in finance and the natural world, showcasing their enduring significance.
Takeaways
- 🧠 Mathematics is deeply intertwined with nature, with patterns like the Fibonacci sequence found in various natural phenomena.
- 🌼 The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones, starting from 0 or 1.
- 🌐 The sequence was studied by ancient Indian mathematicians and later popularized in Europe by Leonardo Fibonacci.
- 📚 Fibonacci's influence is significant, as he contributed to the spread of the Hindu-Arabic numeral system in the Western world through his book, 'Liber Abaci'.
- 🐰 The Fibonacci sequence can be illustrated with a hypothetical problem involving the population growth of rabbits, leading to a prediction of 233 pairs or 466 rabbits after a year.
- 📏 The Fibonacci sequence can be visualized geometrically, forming a spiral that is prevalent in nature, art, architecture, and even the human body.
- 📐 Dividing two consecutive Fibonacci numbers yields the Golden Ratio, approximately 1.618, which is considered aesthetically pleasing and is found in various natural and man-made structures.
- 🎨 The Golden Ratio has been used in art and architecture to create balanced and harmonious compositions, as seen in the works of Renaissance masters like Leonardo da Vinci and Michelangelo.
- 🎶 Even music has been influenced by the Golden Ratio, with evidence of its use in the compositions of famous classical musicians like Debussy, Mozart, Beethoven, and Bach.
- 🌳 Nature exhibits the Fibonacci sequence and Golden Ratio in the branching patterns of trees, spirals on snails, and the structure of galaxies.
- 📈 The Fibonacci sequence and Golden Ratio have practical applications in finance, assisting analysts in predicting and understanding market trends.
Q & A
What is the main idea presented in the video script?
-The main idea is that mathematics, specifically the Fibonacci sequence and the Golden Ratio, are inherently present in nature and have been utilized in various fields such as art, architecture, and even biology.
What is the Fibonacci sequence and how is it formed?
-The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones, usually starting with 0 and 1. It appears in various natural phenomena and has been studied by mathematicians for centuries.
Who are some of the early investigators of the Fibonacci sequence mentioned in the script?
-Early investigators of the Fibonacci sequence include Indian mathematicians Pingala, Virahanka, and Hemachandra.
How was the Fibonacci sequence popularized in Europe?
-The Fibonacci sequence was popularized in Europe by Leonardo of Pisa, also known as Leonardo Fibonacci, who introduced it through his book 'Liber Abaci' or 'Book of Calculation'.
What problem did Fibonacci solve in his book that led to the discovery of the Fibonacci sequence?
-Fibonacci solved a problem involving the idealized growth of a rabbit population, which led to the discovery of the Fibonacci sequence as the solution.
What is the significance of the number 233 in the context of the rabbit population problem?
-The number 233 represents the total number of rabbit pairs (or 466 individual rabbits) after one year, based on the assumptions of the rabbit population problem posed by Fibonacci.
What is the Golden Ratio and how is it related to the Fibonacci sequence?
-The Golden Ratio, approximately equal to 1.618, is a mathematical concept that describes a proportional relationship between two quantities. It is related to the Fibonacci sequence because the ratio of consecutive Fibonacci numbers approaches the Golden Ratio as the numbers get larger.
How is the Golden Ratio used in art and architecture?
-The Golden Ratio is used to create aesthetically pleasing and harmonious proportions in art and architecture. It has been employed by artists like Leonardo da Vinci, Michelangelo, and in architectural structures like the Parthenon and the Taj Mahal.
What is the significance of the Golden Ratio in the human body?
-The Golden Ratio is believed to be present in the proportions of the human body, with certain bone structures and measurements conforming to this ratio, which is thought to contribute to perceived beauty and harmony.
How is the Fibonacci sequence and the Golden Ratio applied in the field of finance?
-In finance, the Fibonacci sequence and the Golden Ratio are used by analysts to predict and understand market trends and patterns, providing a mathematical approach to investment strategies.
What is the connection between the Fibonacci sequence and the background music in the video?
-The background music in the video is composed based on the Fibonacci sequence, illustrating the application of mathematical patterns in creative fields like music.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

Math in the Modern World Module 1 - Nature of Mathematics

Evidence for God: The Fibonacci Sequence

NATURES MATHEMATICS PART-1 1080p HD DOCUMENTARY
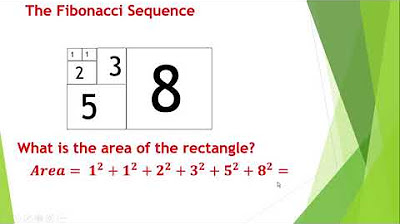
Fibonacci Sequence

PART 3: PATTERNS AND NUMBERS IN NATURE AND THE WORLD || MATHEMATICS IN THE MODERN WORLD

The Wonders of Creation reveal God's Glory - Patterns
5.0 / 5 (0 votes)
