Similar triangles to prove that the slope is constant for a line | Algebra I | Khan Academy

Summary

This video script explores the concept of slope in algebra using geometry. It demonstrates that the slope of a line remains constant by proving the similarity of triangles formed between any two points on the line. The argument relies on the congruence of corresponding angles, established through the properties of parallel lines and transversals.

Takeaways

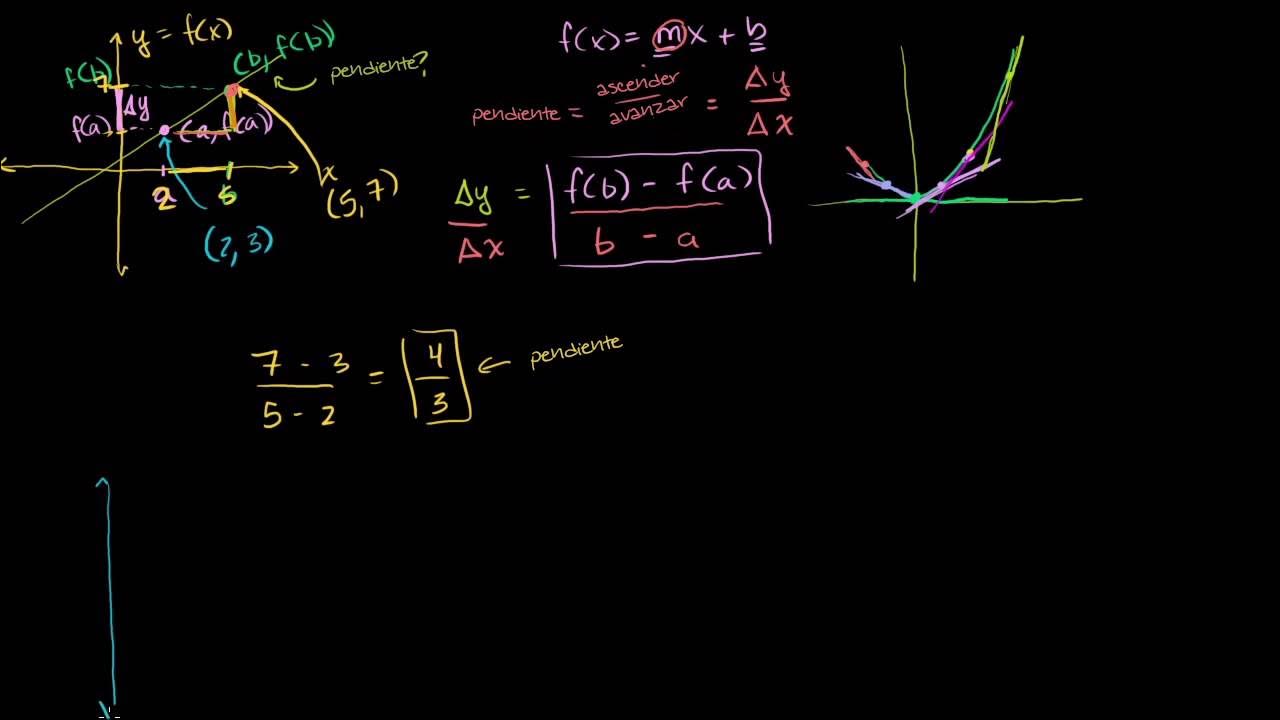
• 📚 The concept of a line in algebra is characterized by a constant rate of change of y with respect to x, which is also known as a constant slope.
• 📐 Slope is defined as the ratio of the change in y (delta y) to the change in x (delta x), indicating the line's inclination.
• 🔍 The video aims to prove the constancy of slope using similar triangles from geometry.
• 📏 Two sets of points are considered to demonstrate the change in x and y, highlighting how these changes relate to the slope.
• 🔄 The ratio of the change in y to the change in x must be the same for any two sets of points on a line to prove the slope's constancy.
• 🔺 The script introduces the idea of similarity in triangles, where corresponding angles must be equal or congruent for triangles to be considered similar.
• 🔶 Demonstrating similarity between two triangles allows for the establishment of a constant ratio between corresponding sides, which is crucial for proving the constant slope.
• 📏 The script uses the properties of parallel lines and transversals to show that the angles formed by the intersection of the line segments are congruent.
• 🔄 By establishing that the triangles formed by the line segments are similar, the script concludes that the ratio of the vertical to horizontal side lengths (the slope) is constant.
• 🔍 The constancy of the slope is proven by showing that any right triangles formed between points on the line are similar, thus maintaining a consistent ratio of side lengths.

Q & A

What is the primary concept discussed in the video?

The primary concept discussed in the video is the constant rate of change or constant slope of a line in algebra, and how to prove it using similar triangles from geometry.

What is the Greek letter delta used to represent in the context of the video?

In the context of the video, the Greek letter delta (Δ) is used as a shorthand for 'change in,' specifically representing the change in y (Δy) over the change in x (Δx).

What does the video aim to prove using similar triangles?

The video aims to prove that the ratio of the change in y to the change in x (i.e., the slope) is constant for a line, using the concept of similar triangles in geometry.

How does the video define the slope of a line?

The video defines the slope of a line as the ratio of the change in y (Δy) to the change in x (Δx), which is a constant value for a straight line.

What is the significance of the triangles being similar in the video's argument?

The significance of the triangles being similar is that it allows the video to establish that the ratio of corresponding sides (which represents the slope) is the same for any two sets of points on the line, proving the constancy of the slope.

What are the conditions for two triangles to be considered similar?

Two triangles are considered similar if all corresponding angles are congruent, or if the ratio of corresponding sides is the same.

How does the video use parallel lines and transversals to prove the similarity of triangles?

The video uses the fact that the horizontal and vertical lines are parallel to each other and that the line connecting the points on the line acts as a transversal. This setup shows that corresponding angles are congruent, thus proving the similarity of the triangles.

What is the role of the horizontal and vertical lines in the video's argument?

The horizontal and vertical lines serve as the basis for creating right triangles. They are parallel to each other, which allows the video to use the properties of parallel lines and transversals to prove the similarity of triangles formed by any two points on the line.

How does the video conclude that the slope is constant for a line?

The video concludes that the slope is constant for a line by showing that any right triangles formed between points on the line are similar. Since the ratio of corresponding sides (the slope) is the same for similar triangles, the slope remains constant.

What is the practical application of understanding the constant slope of a line?

Understanding the constant slope of a line is crucial in algebra and geometry as it helps in analyzing linear relationships, predicting outcomes in linear equations, and understanding the behavior of linear functions.

Outlines

00:00

📚 Understanding Slope Through Geometry

This paragraph introduces the concept of slope in algebra and its geometric interpretation. The speaker explains that a line has a constant rate of change, represented by the Greek letter delta (Δ), which stands for 'change in'. The focus is on proving that the slope remains constant using similar triangles from geometry. The explanation involves selecting two sets of points on a line and demonstrating that the ratio of the change in y (vertical change) to the change in x (horizontal change) is consistent across different points. This consistency is crucial in establishing that the slope, or the ratio of these changes, remains the same for a line.

05:02

🔍 Proving Slope Constancy with Similar Triangles

In this paragraph, the speaker delves deeper into proving that the slope of a line is constant by using the concept of similar triangles. The argument begins by identifying that the triangles formed by the points on the line are right triangles, sharing a common 90-degree angle. The speaker then uses the properties of parallel lines and transversals to demonstrate that the other angles in the triangles are also congruent. By establishing that the triangles are similar, the speaker shows that the ratio of corresponding sides, which corresponds to the slope, remains constant. This proof is essential in understanding why the slope of a line does not change, reinforcing the algebraic concept of a constant rate of change.

Keywords

💡Algebra

Algebra is a branch of mathematics that deals with symbols and the rules for manipulating these symbols. It is often used to describe mathematical relationships between quantities. In the video, algebra is mentioned in the context of understanding the concept of a line having a constant rate of change, which is a fundamental algebraic concept.

💡Line

A line in geometry is a straight one-dimensional figure with no thickness and extends infinitely in both directions. In the video, the line is used to illustrate the concept of slope, which is a measure of the steepness of the line. The video discusses how the slope of a line remains constant, which is a key characteristic of linear functions in algebra.

💡Rate of Change

The rate of change refers to how quickly one quantity changes relative to another. In the context of the video, the rate of change is used to describe the slope of a line, which is the change in y (vertical change) over the change in x (horizontal change). This concept is crucial in understanding how the slope remains constant for a given line.

💡Slope

Slope is a measure of the steepness of a line, calculated as the ratio of the vertical change (rise) to the horizontal change (run). The video emphasizes that the slope of a line is constant, which is proven using the concept of similar triangles. This constant slope is a defining characteristic of linear equations in algebra.

💡Similar Triangles

Similar triangles are triangles that have the same shape but may differ in size. In the video, the concept of similar triangles is used to prove that the slope of a line is constant. By showing that two triangles formed by points on a line are similar, the video demonstrates that the ratio of their sides (which corresponds to the slope) is the same.

💡Change in x

Change in x, often denoted as delta x, refers to the horizontal distance between two points on a line. In the video, the change in x is used to calculate the slope of the line, as it represents the run in the ratio of rise over run. The script discusses how this change is part of the calculation for determining the slope.

💡Change in y

Change in y, often denoted as delta y, refers to the vertical distance between two points on a line. In the video, the change in y is used in conjunction with the change in x to determine the slope of the line. The script explains that the ratio of delta y to delta x is what defines the slope.

💡Greek Letter Delta

The Greek letter delta (Δ) is used in mathematics to denote the change in a quantity. In the video, delta is used to represent the change in y (Δy) and change in x (Δx), which are essential in calculating the slope of a line. The script uses delta to illustrate the concept of change in the context of linear equations.

💡Parallel Lines

Parallel lines are lines in a plane that do not intersect and are always the same distance apart. In the video, the concept of parallel lines is used to establish that the angles formed by a transversal with these lines are congruent. This is crucial in proving that the triangles formed by points on a line are similar.

💡Transversal

A transversal is a line that intersects two or more other lines. In the video, the transversal is used to show that angles formed by parallel lines are congruent, which helps in proving the similarity of triangles. This is a key step in demonstrating that the slope of a line is constant.

💡Corresponding Angles

Corresponding angles are angles that are in the same relative position at each intersection where a transversal crosses two parallel lines. In the video, the concept of corresponding angles is used to establish that the triangles formed by points on a line are similar, which is essential for proving that the slope is constant.

Highlights

Algebra class teaches that a line has a constant rate of change of y with respect to x, or a constant slope.

Slope is defined as the change in y (delta y) over the change in x (delta x).

The video aims to prove the constancy of slope using similar triangles from geometry.

Two sets of points are considered to demonstrate the change in x and y.

The ratio of change in y to change in x is shown to be constant for a line.

Similar triangles are used to prove that the ratio of corresponding sides is the same.

Two triangles are similar if all corresponding angles are congruent.

Triangles with 30, 60, and 90 degrees are shown as similar despite different side lengths.

Similar triangles allow for the establishment of a constant ratio between corresponding sides.

The constancy of slope is proven by showing that any two right triangles formed on a line are similar.

Both triangles are right triangles, sharing one right angle.

Parallel lines and transversals are used to show that other angles are congruent.

The orange line acts as a transversal, showing that corresponding angles are congruent.

The constancy of the slope is established by proving the similarity of triangles formed by any two points on the line.

The ratio of the vertical line segment to the horizontal line segment is constant, defining the slope.

The slope is constant for a line, as demonstrated by the similarity of triangles.

Transcripts

We tend to be told in algebra class that if we have a line,

our line will have a constant rate of change of y

with respect to x.

Or another way of thinking about it,

that our line will have a constant inclination,

or that our line will have a constant slope.

And our slope is literally defined as your change

in y-- this triangle is the Greek letter delta.

It's a shorthand for "change in."

It means change in y-- delta y means change in y--

over change in x.

And if you're dealing with a line, this right over here

is constant for a line.

What I want to do in this video is

to actually prove that using similar triangles

from geometry.

So let's think about 2 sets of 2 points.

So let's say that's a point there.

Let me do it in a different color.

Let me start at this point.

And let me end up at that point.

So what is our change in x between these 2 points?

So this point's x value is right over here.

This point's x value is right over here.

So our change in x is going to be that right over there.

And what's our change in y?

Well, this point's y value is right over here.

This point's y value's right over here.

So this height or this height is our change in y.

So that is our change in y.

Now, let's look at 2 other points.

Let's say I have this point and this point right over here.

And let's do the same exercise.

What's the change in x?

Well, let's see.

If we're going-- this point's x value's here.

This point's x value's here.

So if we start here and we go this far,

this would be the change in x between this point

and this point.

And this is going to be the change--

let me do that in the same green color.

So this is going to be the change in x between those two

points.

And our change in y, well, this y value is here.

This y value's up here.

So our change in y is going to be that right over here.

So what I need to show-- I'm just

picking 2 arbitrary points.

I need to show that the ratio of this change in y

to this change of x is going to be

the same as the ratio of this change in y

to this change of x.

Or the ratio of this purple side to this green side

is going to be the same as the ratio

of this purple side to this green side.

Remember, I'm just picking 2 sets of arbitrary points here.

And the way that I will show it is through similarity.

If I can show that this triangle is similar to this triangle,

then we are all set up.

And just as a reminder of what similarity is,

2 triangles are similar-- and there's multiple ways

of thinking about it-- if and only

if all corresponding-- or I should say,

all three angles are the same, or are congruent.

And let me be careful here.

They don't have to be the same exact angle.

The corresponding angles have to be the same.

So corresponding-- I always misspell

it-- angles are going to be equal.

Or we could say they are congruent.

So for example, if I have this triangle right over here.

And this is 30, this is 60, and this is 90.

And then I have this triangle right over here.

I'll try to draw it-- so I have this triangle,

where this is 30 degrees, this is 60 degrees,

and this is 90 degrees.

Even though their side lengths are different,

these are going to be similar triangles.

They're essentially scaled up versions of each other.

All the corresponding angles-- 60 corresponds

to this 60, 30 corresponds to this 30,

and 90 corresponds to this 1.

So these 2 triangles are similar.

And what's neat about similar triangles,

if you can establish that 2 triangles are similar,

then the ratio between corresponding sides

is going to be the same.

So if these 2 are similar, then the ratio

of this side to this side is going

to be the same as the ratio of-- let

me do that pink color-- this side to this side.

And so you can see why that will be

useful in proving that the slope is constant here,

because all we have to do is look.

If these 2 triangles are similar,

then the ratio between corresponding sides

is always going to be the same.

We've picked 2 arbitrary sets of points.

Then this would be true, really, for any 2 arbitrary set

of points across the line.

It would be true for the entire line.

So let's try to prove similarity.

So the first thing we know is that both of these

are right triangles.

These green lines are perfectly horizontal.

These purple lines are perfectly vertical

because the green lines literally

go in the horizontal direction.

The purple lines go in the vertical direction.

So let me make sure that we mark that.

So we know that these are both right angles.

So we have 1 corresponding angle that is congruent.

Now we have to show that the other ones are.

And we can show that the other ones

are using our knowledge of parallel lines

and transversals.

Let's look at these 2 green lines.

So I'll continue them.

These are line segments, but if we view them as lines

and we just continue them, on and on and on.

So let me do that, just like here.

So this line is clearly parallel to that 1.

They essentially are perfectly horizontal.

And now you can view our orange line as a transversal.

And if you view it as a transversal,

then you know that this angle corresponds to this angle.

And we know from transversals of parallel lines

that corresponding angles are congruent.

So this angle is going to be congruent to that angle

right over there.

Now, we make a very similar argument for this angle,

but now we use the 2 vertical lines.

We know that this segment, we could continue it as a line.

So we could continue it, if we wanted, as a line,

so just like that, a vertical line.

And we could continue this one as a vertical line.

We know that these are both vertical.

They're just measuring-- they're exactly

in the y direction, the vertical direction.

So this line is parallel to this line right over here.

Once again, our orange line is a transversal of it.

And this angle corresponds to this angle right over here.

And there we have it.

They're congruent.

Corresponding angles of the transversal of 2 parallel lines

are congruent.

We learned that in geometry class.

And there you have it.

All of the corresponding-- this angle

is congruent to this angle.

This angle is congruent to that angle.

And then both of these are 90 degrees.

So both of these are similar triangles.

Just let me write that down so we

know that these are both similar triangles.

And now we can use the common ratio of both sides.

So for example, if we called this side length a.

And we said that this side has length b.

And we said this side has length c.

And this side has length d.

We know for a fact that the ratio,

because these are similar triangles,

between corresponding sides, the ratio of a to b

is going to be equal to the ratio of c to d.

And that ratio is literally the definition

of slope, your change in y over your change in x.

And this is constant because any right triangles

that you generate between these two points,

we've just shown that they are going to be similar.

And if they are similar, then the ratio

of the length of this vertical line

segment to this horizontal line segment is constant.

That is the definition of slope.

So the slope is constant for a line.