Ex 6: Conic Section: Parabola with Horizontal Axis and Vertex NOT at the Origin (Right)
Summary
TLDREn este video, se explica cómo graficar la ecuación estándar de una parábola cuya vértice no está en el origen y que abre hacia la izquierda o derecha. Se aborda la importancia de identificar la forma de la ecuación y cómo determinar si la parábola se abre a la derecha o a la izquierda dependiendo del valor de 'A'. Se explica la ubicación del vértice, el foco, la directriz, el eje de simetría y los puntos finales de la recta focal. Al final, se realiza un esbozo más preciso de la parábola, mostrando los conceptos clave de manera clara y didáctica.
Takeaways
- 😀 El primer paso es reconocer que la ecuación dada corresponde a una parábola cuyo vértice no está en el origen y que se abre a la izquierda o derecha.
- 😀 La ecuación de la parábola está en la forma estándar en la que la parte de 'Y' está al cuadrado y la de 'X' está a la primera potencia, lo que indica una parábola con eje horizontal.
- 😀 Si la ecuación tuviera la forma en la que 'X' está al cuadrado y 'Y' a la primera potencia, la parábola tendría un eje vertical y se abriría hacia arriba o abajo.
- 😀 Si 'A' es positivo, la parábola se abre hacia la derecha; si 'A' es negativo, la parábola se abre hacia la izquierda.
- 😀 El vértice de la parábola tiene coordenadas (H, K), donde H y K se obtienen a partir de la ecuación dada.
- 😀 En este ejemplo, el vértice tiene coordenadas (-1, 2), ya que la ecuación contiene el término 'X + 1' y 'Y = 2'.
- 😀 La distancia desde el vértice al foco es igual al valor absoluto de 'A', en este caso 2 unidades, y la parábola se abre a la derecha.
- 😀 El foco se encuentra 2 unidades a la derecha del vértice y sus coordenadas son (1, 2).
- 😀 La directriz es una línea vertical que está a 2 unidades a la izquierda del vértice, y su ecuación es X = -3.
- 😀 El eje de simetría de la parábola es una línea horizontal que pasa por el vértice y el foco, y su ecuación es Y = 2.
- 😀 La longitud del latus rectum es igual al valor absoluto de 4A, lo que da como resultado 8 unidades, y los puntos finales del latus rectum son (1, 6) y (1, -2).
Q & A
¿Cuál es la forma estándar de la ecuación de una parábola cuando el vértice no está en el origen y la parábola se abre hacia la izquierda o la derecha?
-La forma estándar es la ecuación en la que el término 'y' está al cuadrado y el término 'x' está a la primera potencia. Esto indica que la parábola tiene un eje horizontal y se abre hacia la izquierda o la derecha, dependiendo del signo de 'A'.
¿Por qué una parábola se abre hacia la izquierda o hacia la derecha en lugar de hacia arriba o hacia abajo?
-Una parábola se abre hacia la izquierda o la derecha cuando el término 'y' está al cuadrado, lo que genera un eje horizontal. En contraste, si el término 'x' estuviera al cuadrado, la parábola se abriría hacia arriba o hacia abajo, creando un eje vertical.
¿Cómo se determina si la parábola se abre hacia la izquierda o hacia la derecha?
-El signo del valor 'A' determina la dirección de apertura de la parábola. Si 'A' es positivo, la parábola se abre hacia la derecha. Si 'A' es negativo, la parábola se abre hacia la izquierda.
¿Qué representa el valor 'A' en la ecuación estándar de la parábola?
-El valor 'A' en la ecuación estándar de la parábola determina la apertura de la parábola. También está relacionado con la distancia entre el vértice y el foco, así como con la longitud del latus rectum (el diámetro focal).
¿Cómo se encuentra el vértice de la parábola en una ecuación dada?
-El vértice de la parábola tiene las coordenadas (H, K). En la ecuación, el valor de 'H' es el opuesto del valor en el término '(x + H)' y 'K' es el valor en el término 'y = K'.
¿Qué es el foco de una parábola y cómo se encuentra?
-El foco es un punto dentro de la parábola que se encuentra a una distancia de 'A' unidades del vértice, en la dirección en la que la parábola se abre. Si 'A' es positivo, el foco estará a la derecha del vértice, y si 'A' es negativo, estará a la izquierda.
¿Cómo se determina la ecuación de la directriz de la parábola?
-La directriz es una línea vertical que se encuentra a la misma distancia del vértice que el foco, pero en la dirección opuesta. Si el foco está a la derecha del vértice, la directriz estará a la izquierda, y viceversa. La ecuación de la directriz es 'x = V - A', donde 'V' es la coordenada 'x' del vértice y 'A' es el valor asociado con la parábola.
¿Qué es el eje de simetría de la parábola?
-El eje de simetría es una línea que corta la parábola por la mitad y pasa por el vértice y el foco. En una parábola que se abre hacia la derecha o hacia la izquierda, el eje de simetría es una línea horizontal cuya ecuación es 'y = K', donde 'K' es la coordenada 'y' del vértice.
¿Qué es el latus rectum y cómo se calcula?
-El latus rectum, también llamado diámetro focal, es un segmento de línea paralelo a la directriz que pasa por el foco y tiene su longitud igual a '4A'. Su longitud se utiliza para encontrar los puntos extremos del latus rectum, que son puntos de la parábola que están a una distancia de '2A' unidades arriba y abajo del foco.
¿Cómo se encuentran los puntos finales del latus rectum?
-Los puntos finales del latus rectum se encuentran sumando y restando '2A' al valor de la coordenada 'y' del foco. En el caso de este ejemplo, si el foco tiene coordenadas (1, 2), los puntos finales del latus rectum serán (1, 6) y (1, -2), ya que '2 + 4 = 6' y '2 - 4 = -2'.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
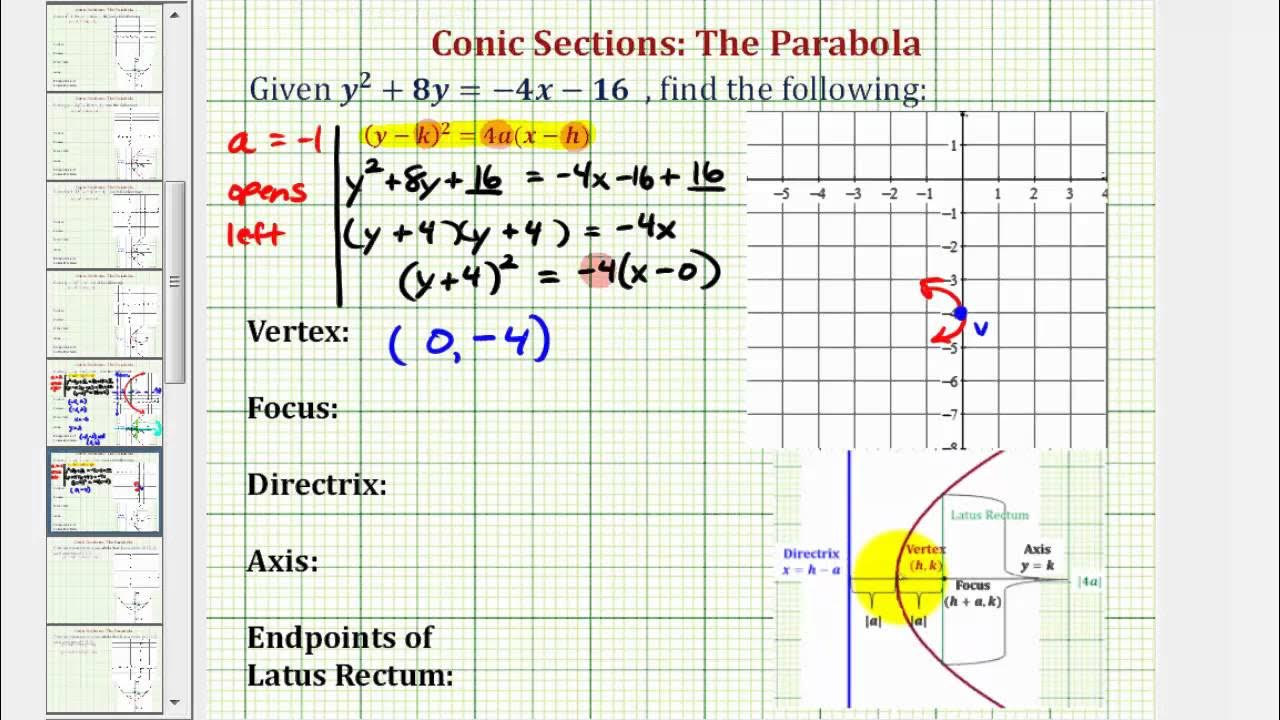
Ex 10: Conic Section: Parabola with Horizontal Axis and Requires Completing the Square (Left)

Ex 2: Conic Section: Parabola with Vertical Axis and Vertex NOT at the Origin (Down)

Ecuación de la parábola | Gráfica y ecuación conociendo vértice y foco Ejemplo 1

Ecuación de la parábola con vértice en el origen y directriz y=-10

Shifted Conics | Parabolas where the Vertex is not the Origin, Finding Focus and Directrix

Exercise 1 Parabola
5.0 / 5 (0 votes)
