工程數學-阻尼震盪

Summary

This presentation explores damped oscillation, a phenomenon where energy loss in an oscillating system leads to a gradual decrease in amplitude until motion ceases. It introduces the damping ratio, a key factor in system response, and distinguishes between under-damped, critically-damped, and over-damped systems. The formula derivation for spring-damped oscillation is explained, using Newton's Second Law and the natural frequency of the system. The presentation concludes with simulations and graphs to illustrate the behavior of different damping scenarios, emphasizing the importance of damping in system stability.

Takeaways

• 📚 Damping is the loss of energy in an oscillating system due to dissipation, which can be caused by internal or external factors like fluid resistance or surface friction.
• 🔍 Damped oscillation is a process where mechanical energy is gradually converted into internal energy, causing the amplitude of oscillation to decrease until it stops.
• 📏 The damping ratio, denoted by Theta, is a dimensionless measure that describes how oscillations decay after a disturbance and characterizes the frequency response of a system.
• 🔄 Systems with higher damping ratios demonstrate more of a damping effect, and the damping ratio can vary from over-damped, under-damped, to critically damped.
• 🔍 Over-damped systems have an amplitude that decreases monotonically over time without oscillating, while critically damped systems return to equilibrium as quickly as possible without oscillating.
• 🔄 Under-damped systems exhibit damped oscillations where the amplitude decreases over time before eventually returning to equilibrium.
• 📐 In spring-damped oscillation, a block of mass m attached to a spring with spring constant K oscillates on a horizontal surface influenced by damping forces and the spring's restoring force.
• 🧩 Newton's Second Law is used to derive the formula for spring-damped oscillation by calculating the resultant force of friction and the spring force.
• 🔢 The characteristic equation is derived from the second-order linear homogeneous differential equation, which helps determine the type of damping based on the values of Zeta (damping ratio).
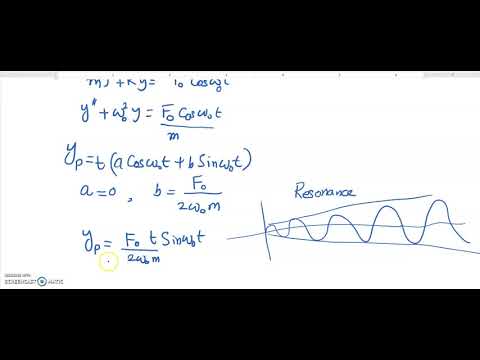
• 📈 The formula for the position of the oscillating system over time, X(t), is derived based on the type of damping, with different formulas for under-damped, critically damped, and over-damped cases.
• 📊 MB (presumably a software or method) is used to perform simulations, set parameters, define motion equations, and analyze the motion to generate X-T and V-T plots.
• 🔚 The conclusion emphasizes that under-damped oscillation is not periodic due to amplitude decay, and over-damped systems take longer to return to equilibrium due to stronger resistance compared to critically damped systems.

Q & A

What is damped oscillation?

Damped oscillation refers to the phenomenon where an oscillating system experiences a loss of energy due to dissipative forces, such as fluid resistance or friction, which cause the amplitude of oscillation to gradually decrease until the oscillation stops.

What causes damping in an oscillating system?

Damping in an oscillating system is caused by internal or external factors such as fluid resistance, surface friction, or resistance in electronic oscillators, which lead to energy dissipation and a reduction in amplitude.

What is the role of the damping ratio in oscillation?

The damping ratio, denoted by Theta, is a dimensionless measure that describes how the oscillations in a system decay after a disturbance. It characterizes the frequency response of a second-order ordinary differential equation.

How does the damping ratio influence the behavior of an oscillating system?

Systems with higher damping ratios demonstrate more damping effect. The damping ratio can vary, and it influences whether a system is over-damped, under-damped, or critically damped.

What are the characteristics of an over-damped system?

In an over-damped system, the amplitude decreases monotonically over time, and the system slowly returns to equilibrium without oscillating.

What happens in a critically damped system?

In a critically damped system, the system returns to the equilibrium position as quickly as possible without oscillating, and it stabilizes rapidly.

Describe the behavior of an under-damped system.

In an under-damped system, the system exhibits damped oscillations where the amplitude decreases over time and eventually returns to the equilibrium position.

What is the significance of the spring-mass-damper system in the context of damped oscillation?

The spring-mass-damper system is a classic example of damped oscillation, where a block of mass attached to a spring oscillates on a horizontal surface influenced by damping forces such as friction and the spring's restoring force.

How is the motion equation derived for a spring-mass-damper system?

The motion equation for a spring-mass-damper system is derived by introducing Newton's Second Law, calculating the resultant force of friction and the spring force, and then combining these equations with the damping coefficient and the natural frequency of the system.

What are the different types of roots obtained from the characteristic equation of a damped system?

Depending on the value of the damping ratio (Zeta), the characteristic equation can yield two complex roots (under-damped), repeated roots (critically damped), or two real roots (over-damped).

How can the behavior of a damped oscillation system be visualized?

The behavior of a damped oscillation system can be visualized using graphs such as the displacement-time (XT) plot and velocity-time (VT) plot, which show how the system's response changes over time.

What conclusion can be drawn from the analysis of damped oscillation using formulas and simulations?

The analysis and simulation confirm that under-damped oscillation is not periodic due to amplitude decay. Over-damped systems have a slower return to equilibrium due to stronger resistance compared to critically damped systems.