Getaran Bebas Teredam - Persamaan Gerak
Summary
TLDRThis lecture explores the concepts of free damped vibrations in a spring-mass system with a focus on deriving the governing equations of motion. The instructor introduces undamped vibrations, where the amplitude remains constant, and damped vibrations, where the amplitude gradually decreases over time. Key concepts include the spring constant, damping coefficient, and how they influence system behavior. The lecture covers critically damped and lightly damped systems, followed by the derivation of the governing equations using Newton's second law. The discussion also includes solving these equations to determine the type of damping in the system, providing a solid foundation for vibration analysis in engineering.
Takeaways
- 😀 Free vibration without damping leads to constant amplitude oscillations, as shown in the system with mass and spring.
- 😀 Damped free vibrations occur when a system has a spring and a damper, causing the amplitude to gradually decrease until it stops.
- 😀 There are three types of damping: critical damping, light damping (underdamping), and heavy damping (overdamping).
- 😀 Critical damping results in the quickest return to equilibrium without oscillations, which is ideal for applications like shock absorbers.
- 😀 Light damping (underdamping) allows for oscillations with decreasing amplitude over time, which is commonly observed in real systems.
- 😀 Heavy damping (overdamping) resists movement too much, causing the system to return to equilibrium without oscillations but more slowly.
- 😀 The governing equation for damped free vibrations is: m * x'' + c * x' + k * x = 0, where m is mass, c is damping coefficient, k is spring constant, and x is displacement.
- 😀 The system's response to damping is determined by solving the characteristic equation of the governing differential equation.
- 😀 The discriminant of the quadratic equation from the governing equation determines the type of damping: positive for overdamping, zero for critical damping, and negative for underdamping.
- 😀 Practical examples include calculating spring forces using Hooke’s Law (F = kx) and damping forces using the equation F = c * v, where v is velocity.
- 😀 These damped vibration systems are used in engineering to design stable structures, such as vibration isolators and suspension systems.
Please replace the link and try again.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Getaran Mekanik : penyelesaian soal Getaran Bebas sistem 1 derajat kebebasan dengan peredam

Undamped Free Vibration (Seri Getaran Mekanis part1)

Dinamika Struktur #3: SDOF Getaran Bebas Dengan Redaman
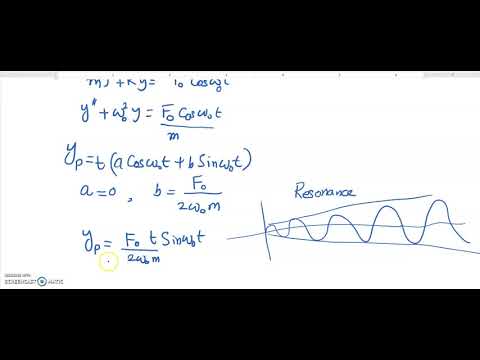
Modeling Forced Oscillations of Mass Spring System clip 3

M H S aula 03

Simple Harmonic Motion(SHM) - Force, Acceleration, & Velocity at 3 Positions
5.0 / 5 (0 votes)