Fluida Dinamis (Fisika SMA/MA Sagufindo kls XI smt 1)

Summary

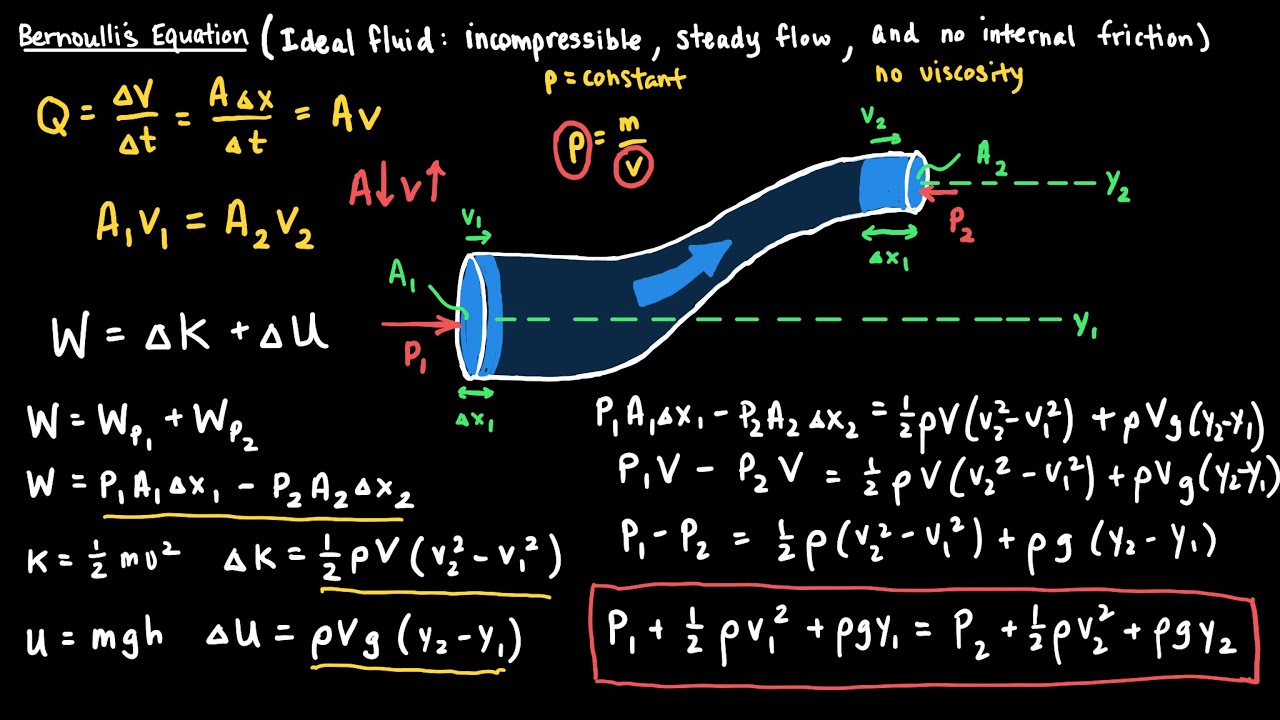
In this educational video, the concept of dynamic fluids or *fluida dinamis* is explored, with a focus on ideal fluid properties such as incompressibility, no friction, and steady flow. The principle of continuity is introduced, demonstrating how fluid velocity changes in pipes with different cross-sectional areas while maintaining a constant flow rate. The video uses clear examples and a mathematical formula to explain how fluid velocity relates to pipe area. This concept is reinforced with practical applications, like the acceleration of water when pressing a hose nozzle, and ends with an example problem for further learning.

Takeaways

• 😀 Fluids in motion are studied under the topic of fluid dynamics, which explores how fluid behavior changes under different conditions.
• 😀 Ideal fluids are assumed to be incompressible, meaning their volume and density remain constant even under pressure.
• 😀 An ideal fluid experiences no friction, allowing for smoother flow without resistance against surfaces.
• 😀 In ideal fluid flow, the movement is steady, with particles following consistent paths and maintaining the same velocity at all times.
• 😀 The Continuity Equation states that the flow rate (debit) remains constant in a closed system, even if the pipe's cross-sectional area changes.
• 😀 The formula for the Continuity Equation is: A1 * V1 = A2 * V2, where A is the cross-sectional area and V is the velocity of the fluid at different points in the pipe.
• 😀 If the cross-sectional area of a pipe decreases, the fluid velocity must increase to maintain a constant flow rate.
• 😀 The reverse is also true: if the cross-sectional area increases, the fluid velocity will decrease.
• 😀 An example is given where fluid flow in pipe A has a velocity of 10 m/s and a cross-sectional area of 10 cm². For pipe B with a smaller area of 4 cm², the velocity increases to 25 m/s.
• 😀 This relationship between fluid velocity and pipe area is fundamental in many applications, including designing fluid transport systems like pipes and hoses.

Q & A

What is the main topic discussed in the video?

The video discusses fluid dynamics, focusing on the principles of fluid flow, the concept of ideal fluid, and the continuity equation.

What is an ideal fluid, and what are its key characteristics?

An ideal fluid is one that is incompressible (its volume and density do not change) and non-viscous (it does not experience internal friction). Its flow is steady and predictable.

What is the formula for calculating the flow rate of a fluid?

The flow rate (Q) is calculated using the formula Q = A × V, where A is the cross-sectional area of the pipe and V is the velocity of the fluid.

What does the principle of continuity state about fluid flow?

The principle of continuity states that in a steady flow, the mass of fluid entering any section of a pipe must equal the mass exiting it. This implies that if the cross-sectional area decreases, the velocity of the fluid must increase.

What is the continuity equation, and how is it written?

The continuity equation is A1 × V1 = A2 × V2, where A1 and A2 are the areas at two different points in the pipe, and V1 and V2 are the fluid velocities at those points.

How does the cross-sectional area of a pipe affect the velocity of fluid flowing through it?

If the cross-sectional area of a pipe decreases, the velocity of the fluid increases. Conversely, a larger area leads to a slower fluid velocity.

What is the relationship between fluid flow rate, area, and velocity?

The fluid flow rate is directly proportional to both the cross-sectional area and the velocity. As the area increases, the velocity decreases to maintain a constant flow rate, and vice versa.

Can you give an example that demonstrates the continuity equation?

Yes, in the video, when the cross-sectional area of a pipe is smaller at one point (like the nozzle of a hose), the velocity of the fluid increases, which is consistent with the continuity equation.

What practical applications are based on the principles of fluid dynamics discussed in the video?

Practical applications include water distribution systems, blood flow in the body, design of pipes and channels, and even tools like garden hoses, where fluid velocity and flow rate are manipulated.

How does the concept of ideal fluid help in simplifying real-world fluid flow problems?

The concept of an ideal fluid helps simplify calculations by assuming no friction and constant density, making it easier to apply equations like the continuity equation to real-world fluid dynamics problems.