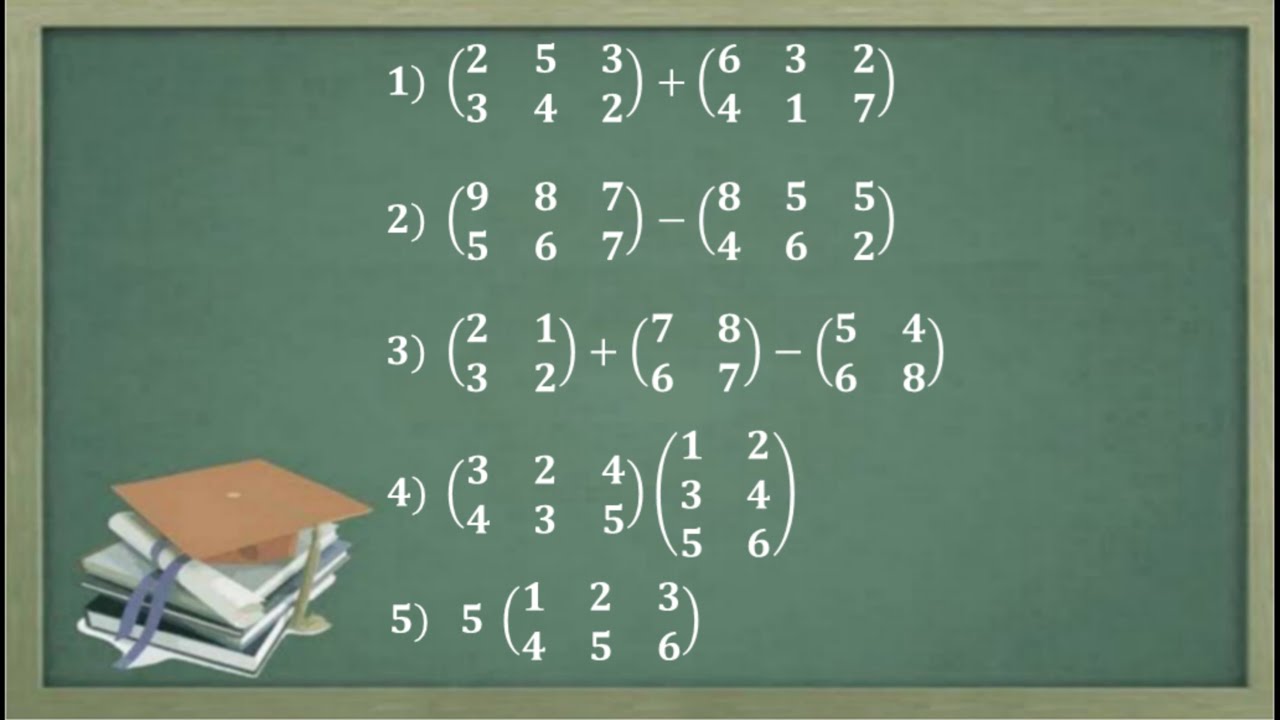Matrices and Matrix Operations shorter
Summary
TLDRThis video tutorial covers fundamental matrix operations, including equality, addition, subtraction, scalar multiplication, and matrix multiplication. It explains how to determine when two matrices are equal, how to perform element-wise addition and subtraction, and how to multiply matrices by a scalar. The tutorial also demonstrates matrix multiplication with step-by-step examples. Viewers will learn how to handle matrices of different sizes, how to compute matrix products, and how these operations can be applied to solve systems of linear equations.
Takeaways
- 😀 Matrices are equal if they have the same size and corresponding entries are equal.
- 😀 Matrix addition and subtraction can only be performed if matrices are of the same size, and it involves adding or subtracting corresponding entries.
- 😀 Scalar multiplication of a matrix involves multiplying every element of the matrix by a scalar.
- 😀 Matrix multiplication is defined when the number of columns in the first matrix equals the number of rows in the second matrix.
- 😀 The product of two matrices results in a new matrix where each element is the sum of the products of corresponding row and column elements.
- 😀 Matrices of different sizes cannot be added or subtracted.
- 😀 A column matrix (vector) has only one column, while a row matrix (vector) has only one row.
- 😀 The size of the product of two matrices is determined by the number of rows of the first matrix and the number of columns of the second matrix.
- 😀 Matrix multiplication follows the rule where each element of the product matrix is the sum of the products of corresponding row and column elements from the original matrices.
- 😀 Matrix operations such as addition, subtraction, scalar multiplication, and multiplication can be used to solve systems of linear equations and analyze linear combinations of vectors.
Q & A
What is the condition for two matrices to be equal?
-Two matrices, A and B, are equal if they have the same size (i.e., the same number of rows and columns) and their corresponding entries are equal.
Can two matrices of different sizes be equal?
-No, two matrices cannot be equal if they are of different sizes. Matrices must have the same dimensions for equality.
What are the operations allowed for two matrices to be added or subtracted?
-Two matrices can be added or subtracted only if they have the same size. The operation is performed element-wise, meaning corresponding entries are added or subtracted.
What happens when two matrices of different sizes are added or subtracted?
-If two matrices have different sizes, the operation is undefined. The addition or subtraction can only occur between matrices of the same size.
How do you perform scalar multiplication on a matrix?
-Scalar multiplication involves multiplying each entry of the matrix by a scalar. For example, if matrix A is multiplied by a scalar c, every element of matrix A is multiplied by c.
What is the result of multiplying a matrix by a negative scalar?
-When a matrix is multiplied by a negative scalar, every element of the matrix is multiplied by the negative scalar, effectively changing the sign of each element.
What are the conditions for matrix multiplication to be defined?
-Matrix multiplication is defined when the number of columns in the first matrix equals the number of rows in the second matrix. The resulting product matrix will have the number of rows of the first matrix and the number of columns of the second matrix.
How do you compute an element of the resulting matrix when multiplying two matrices?
-To compute an element in the resulting matrix, take the dot product of the corresponding row of the first matrix and the corresponding column of the second matrix. This involves multiplying the entries and summing the results.
What happens if the number of columns in the first matrix does not equal the number of rows in the second matrix?
-If the number of columns in the first matrix is not equal to the number of rows in the second matrix, matrix multiplication is undefined. The matrices cannot be multiplied.
How do matrix operations like addition, subtraction, and multiplication apply in solving systems of linear equations?
-Matrix operations like addition, subtraction, and multiplication are used to express and solve systems of linear equations. A system of equations can be written as a matrix equation, and various matrix methods like Gaussian elimination or matrix inversion are used to find the solution.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
5.0 / 5 (0 votes)