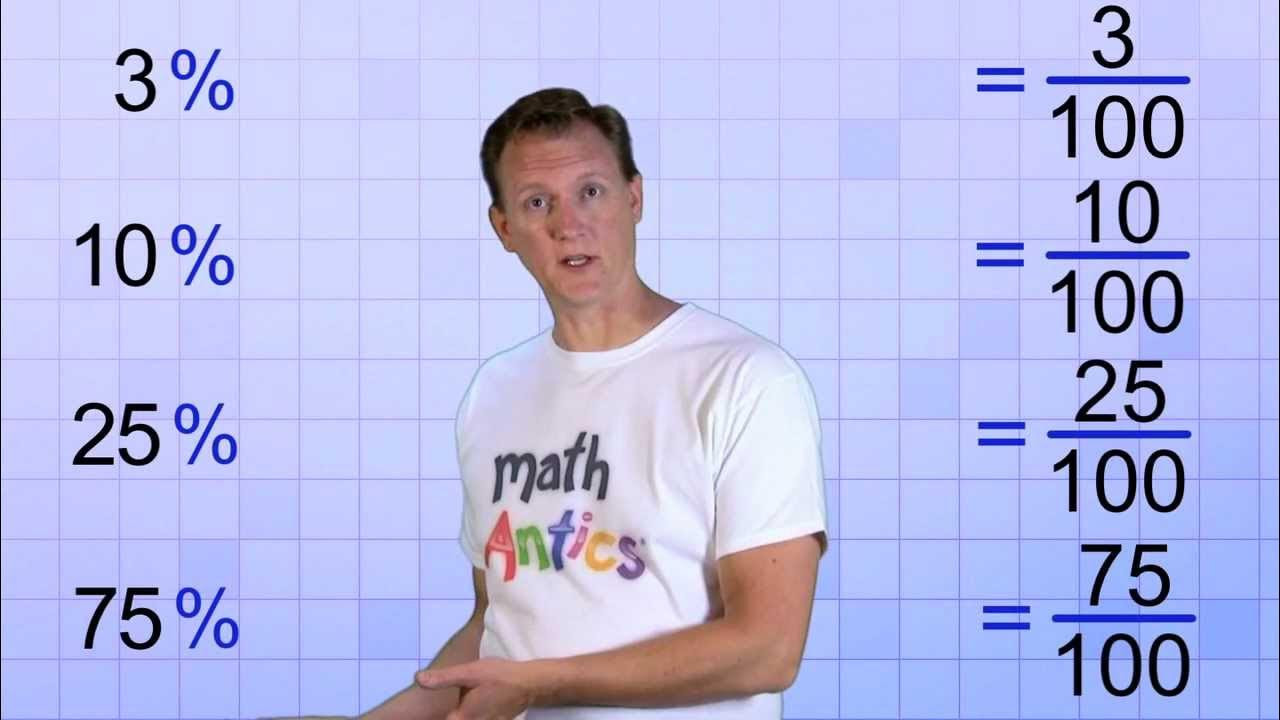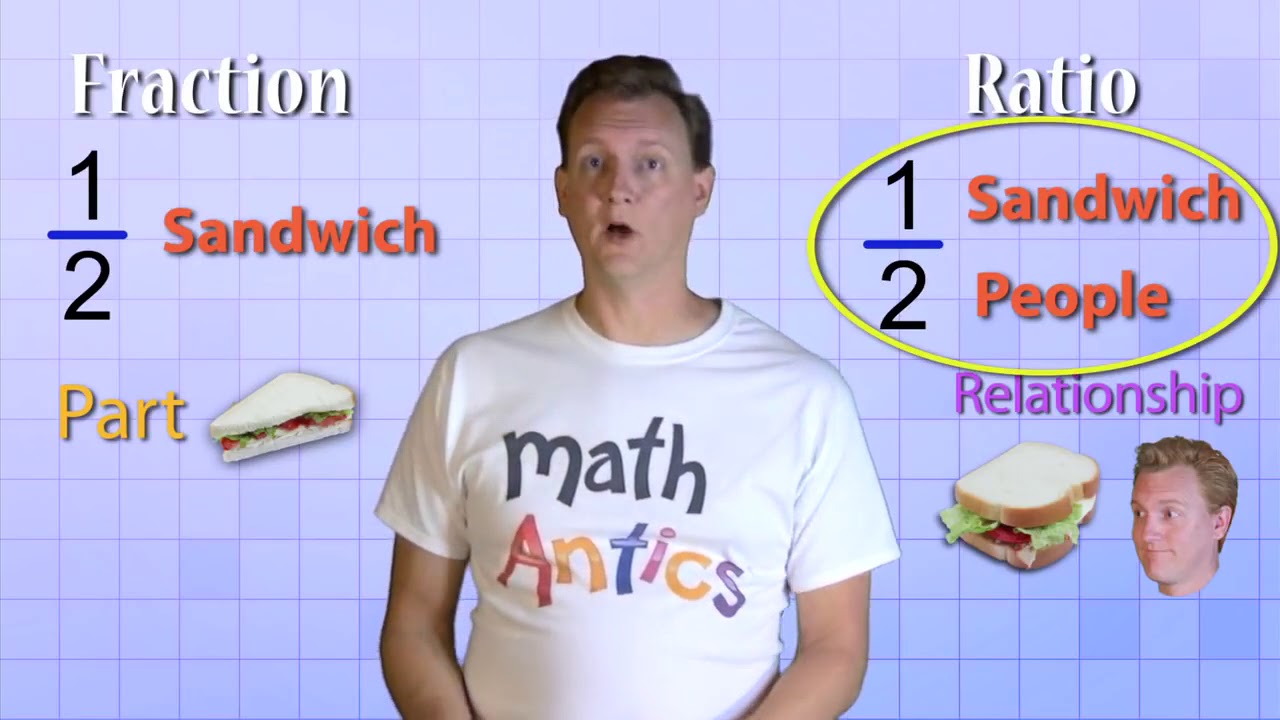MATH 5 || QUARTER 3 WEEK 1 | PERCENT AND ITS RELATIONSHIP TO FRACTIONS, RATIOS, AND DECIMAL NUMBERS
Summary
TLDRThis math lesson introduces students to the concept of percent and its relationship with fractions, ratios, and decimal numbers. Using models and real-life examples, the script explains how percent represents a ratio out of 100, and how it can be expressed as fractions, ratios, and decimals. The lesson includes interactive activities and word problems to help students visualize and identify the base, rate, and percentage in various scenarios, such as shopping discounts, bank interest, and class surveys. The goal is to help students understand percent in practical applications and enhance their problem-solving skills.
Takeaways
- 😀 Percent represents 'per hundred' and can be expressed as a fraction with a denominator of 100, as a ratio, or as a decimal.
- 😀 Percent is symbolized by '%' and is used to compare a certain number to a total of 100, making it easier to express parts of a whole.
- 😀 A visual model, such as a grid of 100 squares, can help illustrate the concept of percent by shading in a certain number of squares.
- 😀 A percentage can be written as a fraction (e.g., 7/100), a ratio (e.g., 7:100), a decimal (e.g., 0.07), or a percent (e.g., 7%).
- 😀 Percentages, fractions, ratios, and decimals are interconnected, and each can be converted into the others for easy comparison and calculation.
- 😀 When solving word problems involving percentages, it's important to identify the rate (percentage), base (total amount), and percentage (part of the total).
- 😀 A real-life example shows that if Veronica and Ron earned 100 pesos and gave 80 pesos to their mother, they gave 80% of their earnings.
- 😀 The rate, base, and percentage formula is: rate × base = percentage, or percentage ÷ base = rate.
- 😀 Learning to identify the base, rate, and percentage in various problems will help apply mathematical concepts to real-life situations.
- 😀 Real-life situations such as shopping discounts, commissions, and earnings can be modeled using percentages, making the concept practical and applicable.
- 😀 In a given problem, such as a discount on a book or percentage of families in fishing, it's important to know which number represents the base, rate, and percentage.
Q & A
What is the relationship between percent, fractions, ratios, and decimals?
-Percent is a special ratio that compares a number to 100. It can be expressed as a fraction (e.g., 7/100), a ratio (e.g., 7:100), and a decimal (e.g., 0.07). Essentially, percent provides an easy way to compare parts of a whole using the base of 100.
How do we express 7% in different forms (fraction, ratio, and decimal)?
-7% can be expressed in the following ways: as a fraction (7/100), as a ratio (7:100), and as a decimal (0.07). In each case, 7% represents 7 parts of 100.
What is the significance of the symbol '%' in a percentage?
-The symbol '%' represents 'per 100'. It is used to replace the denominator of 100 in a fraction, meaning it compares the part to the whole in a way that is easy to understand by simplifying the ratio to 100.
Can you explain how the concept of percent applies to real-life situations?
-Percent is commonly used in real-life situations such as sales discounts, calculating commissions, determining the proportion of a group (e.g., the percentage of students who passed a test), and even understanding nutritional labels on food items.
How do we calculate the percentage of a part in a total?
-To calculate the percentage of a part in a total, divide the part by the whole and multiply by 100. For example, if 7 out of 100 squares are shaded, the percentage is (7/100) * 100 = 7%.
In the example of Veronica and Ron, what percent of their earnings did they give to their mother?
-Veronica and Ron gave 80 pesos out of 100 pesos to their mother. Therefore, the percentage given to their mother is 80% (80/100 * 100 = 80%).
What are the key elements of a percentage problem, and how are they identified?
-A percentage problem involves three key elements: the **base**, the **rate**, and the **percentage**. The base represents the whole (total), the rate is the percentage itself, and the percentage represents the part or amount taken from the whole.
What does it mean to identify the base, rate, and percentage in a given problem?
-Identifying the base means finding the total or whole number in the problem, the rate refers to the percentage value, and the percentage is the part or the actual amount that corresponds to the given rate.
In the word problem about Mrs. Santiago’s class, how do we identify the base, rate, and percentage?
-In the problem, the base is 40 (the total number of pupils), the rate is 75% (the percentage of students who like mathematics), and the percentage is 30 (the number of pupils who are mathematics lovers).
How do you convert a fraction into a decimal and then into a percent?
-To convert a fraction into a decimal, divide the numerator by the denominator. For example, 7/100 = 0.07. To convert this decimal into a percent, multiply by 100, resulting in 7%.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
5.0 / 5 (0 votes)