Cuartiles, Deciles y Percentiles - Datos Agrupados
Summary
TLDREste video ofrece una explicación detallada sobre cómo calcular medidas de tendencia no central, como los cuartiles, deciles y percentiles, utilizando un conjunto de datos de 50 personas. A través de ejemplos prácticos, se enseña cómo dividir los datos en diferentes segmentos (cuartiles en 4 partes, deciles en 10 y percentiles en 100), con el objetivo de comprender mejor la distribución de los valores. Además, se aclara cómo interpretar los resultados y la importancia de estas medidas estadísticas para analizar grandes volúmenes de datos, brindando a los espectadores herramientas clave para entender y aplicar estos conceptos en contextos reales.
Takeaways
- 😀 La mediana divide el conjunto de datos en dos partes iguales, con el 50% de los valores por debajo y el 50% por encima de ella.
- 😀 Los cuartiles dividen un conjunto de datos en cuatro partes iguales, utilizando tres cortes: Q1, Q2 (la mediana) y Q3.
- 😀 Q2 (cuartil 2) es igual a la mediana, y divide los datos en dos mitades con el 50% a la izquierda y el 50% a la derecha.
- 😀 El cuartil 3 (Q3) divide el 75% de los datos por debajo de él, y el 25% restante por encima.
- 😀 Para calcular el cuartil 3, se identifica el intervalo en el que se encuentra el acumulado necesario para llegar al 75% de los datos.
- 😀 Los cuartiles no se dividen en 4 partes iguales, sino que son tres cortes que permiten dividir los datos en cuatro partes.
- 😀 Los deciles dividen los datos en 10 partes iguales usando 9 cortes, lo que permite calcular percentiles en incrementos del 10%.
- 😀 Los deciles funcionan de manera similar a los cuartiles, pero dividen el conjunto de datos en 10 partes iguales, en lugar de 4.
- 😀 El cálculo de los percentiles sigue una fórmula similar a la de los deciles, pero divide los datos en 100 partes iguales, con 99 cortes.
- 😀 Un percentil específico indica el valor por debajo del cual se encuentra un porcentaje dado de la población, como el percentil 70 que indica el 70% de los datos debajo de un valor específico.
Q & A
¿Qué es la mediana y cómo se calcula?
-La mediana es el valor que divide a un conjunto de datos en dos partes iguales. Se calcula ordenando los datos y seleccionando el valor central. Si el número de datos es impar, es el valor medio; si es par, se promedia los dos valores centrales.
¿Cuántos cuartiles existen y qué representan?
-Existen tres cuartiles que dividen un conjunto de datos en cuatro partes iguales. El primer cuartil (Q1) es el valor que divide el 25% inferior, el segundo cuartil (Q2) es la mediana (50%), y el tercer cuartil (Q3) divide el 75% inferior.
¿Cuál es la diferencia entre cuartiles y mediana?
-La mediana divide un conjunto de datos en dos partes iguales, mientras que los cuartiles dividen los datos en cuatro partes iguales. El cuartil 2 es, de hecho, la mediana.
¿Por qué se dicen que los cuartiles son tres y no cuatro?
-Aunque los cuartiles dividen los datos en cuatro partes, solo existen tres cuartiles (Q1, Q2 y Q3), ya que estos tres puntos son los cortes que dividen el conjunto de datos en cuatro segmentos.
¿Cómo se calcula el tercer cuartil (Q3)?
-El tercer cuartil (Q3) se calcula encontrando el valor que divide el 75% inferior de los datos del 25% superior. Se utiliza una fórmula específica que involucra la frecuencia acumulada y los límites de los intervalos.
¿Qué son los deciles y cómo se calculan?
-Los deciles dividen un conjunto de datos en diez partes iguales, utilizando nueve cortes. Se calculan aplicando una fórmula similar a la de los cuartiles, pero dividiendo el total de datos entre 10. Por ejemplo, el cuarto decil (D4) marca el punto donde el 40% de los datos se encuentran por debajo de este valor.
¿Cuál es la fórmula para calcular los deciles?
-La fórmula para calcular los deciles es similar a la de los cuartiles, pero en lugar de dividir el total de datos entre 4, se divide entre 10. Se usa la frecuencia acumulada de los intervalos y la posición de los datos dentro del conjunto.
¿Cómo se determina el percentil 70?
-Para calcular el percentil 70, se utiliza una fórmula similar a la de los deciles. Se multiplica el total de datos (n) por el percentil deseado (en este caso, 70) y luego se divide entre 100. El valor obtenido se localiza en la tabla de frecuencias acumuladas para determinar el intervalo correspondiente.
¿Qué significa un percentil 70 de 52.75 años?
-Un percentil 70 de 52.75 años significa que el 70% de las personas en el conjunto de datos tienen una edad menor a 52.75 años, y el 30% restante tiene una edad superior a este valor.
¿Cómo se calculan los percentiles y qué diferencia tienen con los deciles?
-Los percentiles dividen el conjunto de datos en 100 partes iguales utilizando 99 cortes. La fórmula es similar a la de los deciles, pero en este caso se divide el total de datos entre 100, lo que permite una segmentación más precisa. La principal diferencia con los deciles es que los percentiles dividen los datos en más partes (100) en lugar de 10.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

MEDIDAS DE POSICIÓN (CUARTIL, DECIL, PERCENTIL) - DATOS AGRUPADOS

CUARTILES, DECILES Y PERCENTILES PARA DATOS NO AGRUPADOS

Cuartiles, deciles y percentiles, datos agrupados, no agrupados, medidas de posición

Conceptos estadísticos básicos
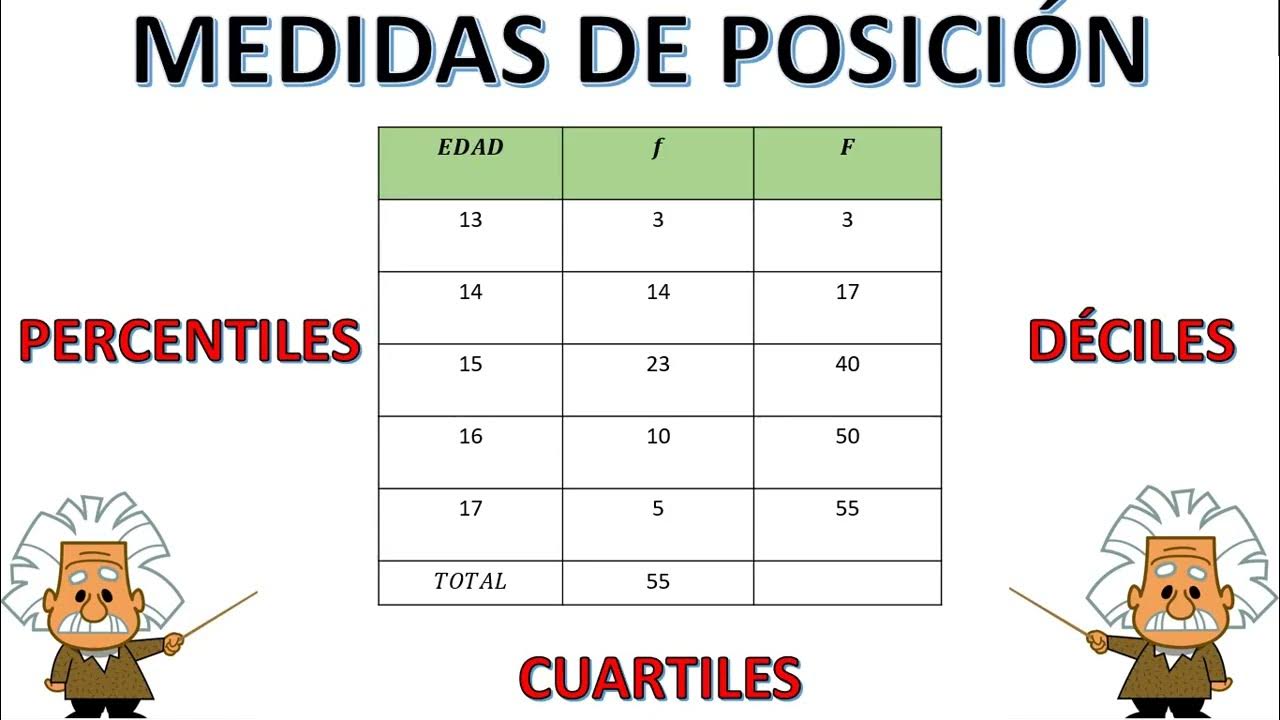
MEDIDAS DE POSICIÓN: PERCENTILES, DECILES Y CUARTILES #estadistica #deciles #percentiles
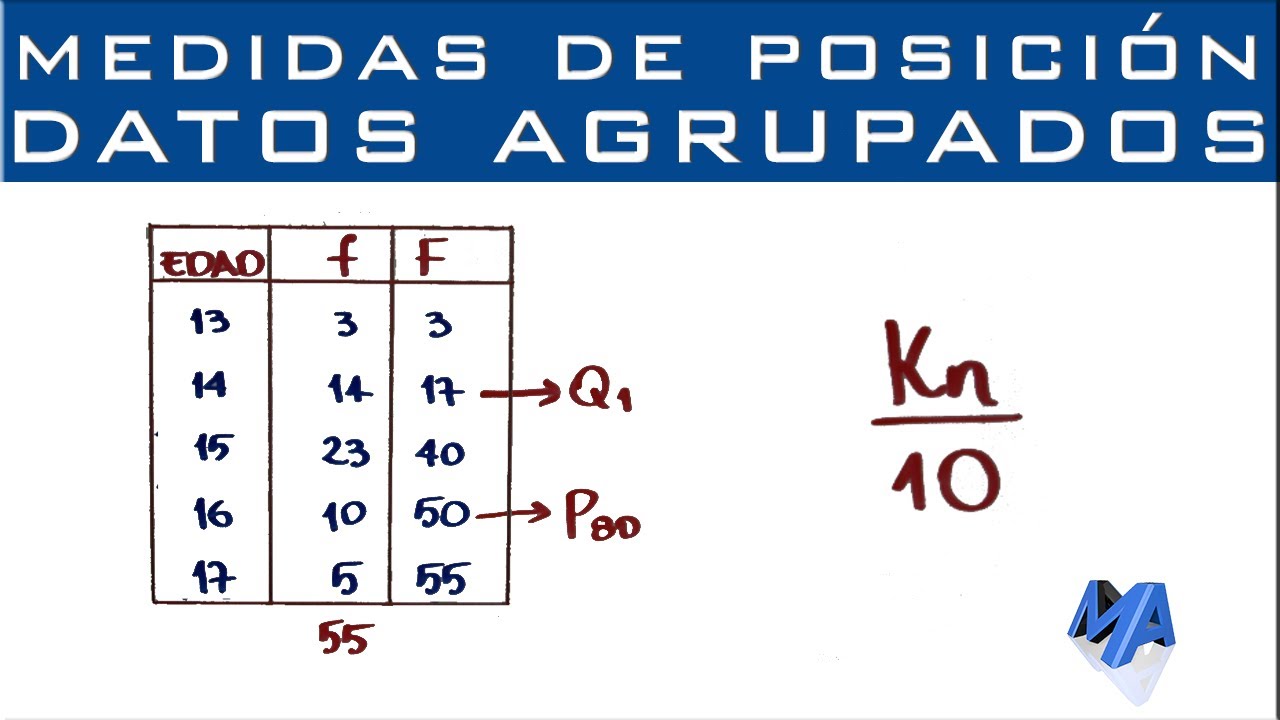
Cuartiles, Deciles y Percentiles | Datos agrupados puntualmente
5.0 / 5 (0 votes)
