9. Vorticity (1 of 2)
Summary
TLDRThis video explores the concept of vorticity in fluid dynamics, explaining how it measures the angular momentum of fluid particles. Through practical demonstrations, the video illustrates the relationship between vorticity, velocity, and fluid flow in various scenarios, such as boundary layers and vortex tanks. It discusses important theorems like Kelvin's and Helmholtz's, and explains how vorticity is influenced by forces like viscosity and body forces. The video also touches on circulation and its role in fluid motion, using real-world analogies like the behavior of fluids in tanks and the Coriolis effect.
Takeaways
- 😀 Vorticity is a measure of the angular momentum of a fluid particle, indicating the rotation of the fluid around its center of mass.
- 😀 The vorticity of a fluid can be visualized through vortex lines, which represent the local axes of spin for the fluid particles.
- 😀 Vorticity is defined as the curl of the velocity vector, and each fluid particle has its own vorticity vector.
- 😀 Vorticity can exist even in straight flows where the fluid does not curve, such as in boundary layers near walls.
- 😀 Viscosity plays a crucial role in creating and modifying vorticity by inducing shear forces that affect the flow, particularly near walls.
- 😀 The vorticity meter can be used to measure local vorticity in a fluid by detecting the angular velocity of fluid elements.
- 😀 In a spiral vortex tank, the net vorticity is zero, even though the flow is curving, because of the opposing rotations in different regions of the vortex.
- 😀 Kuroko's theorem relates vorticity and stagnation pressure, showing that in an incompressible and steady flow, the gradient of stagnation pressure is normal to both the velocity and vorticity vectors.
- 😀 Circulation, defined as the line integral of velocity around a closed curve, is directly related to the vorticity passing through the area bounded by that curve.
- 😀 Coriolis forces, a body force arising from Earth's rotation, influence the circulation in fluids, causing it to increase in the Northern Hemisphere in a counterclockwise direction.
Q & A
What is vorticity in the context of fluid dynamics?
-Vorticity is a measure of the moment of momentum of a small spherical fluid particle about its own center of mass. It quantifies the local rotation of the fluid, which can be understood as the tendency of the fluid particles to spin around an axis.
How is the angular velocity of a solid sphere related to vorticity?
-When a fluid freezes into a solid, the angular velocity of the solid sphere at the moment of freezing is exactly half of the vorticity of the fluid before freezing. This relationship arises due to the conservation of momentum.
What is the role of vortex lines in vorticity?
-Vortex lines are imaginary lines that represent the local axis of spin for fluid particles. These lines are everywhere tangent to the vorticity vector in the fluid, helping to visualize the flow's rotation at different points.
Can vorticity exist in a flow without rotation?
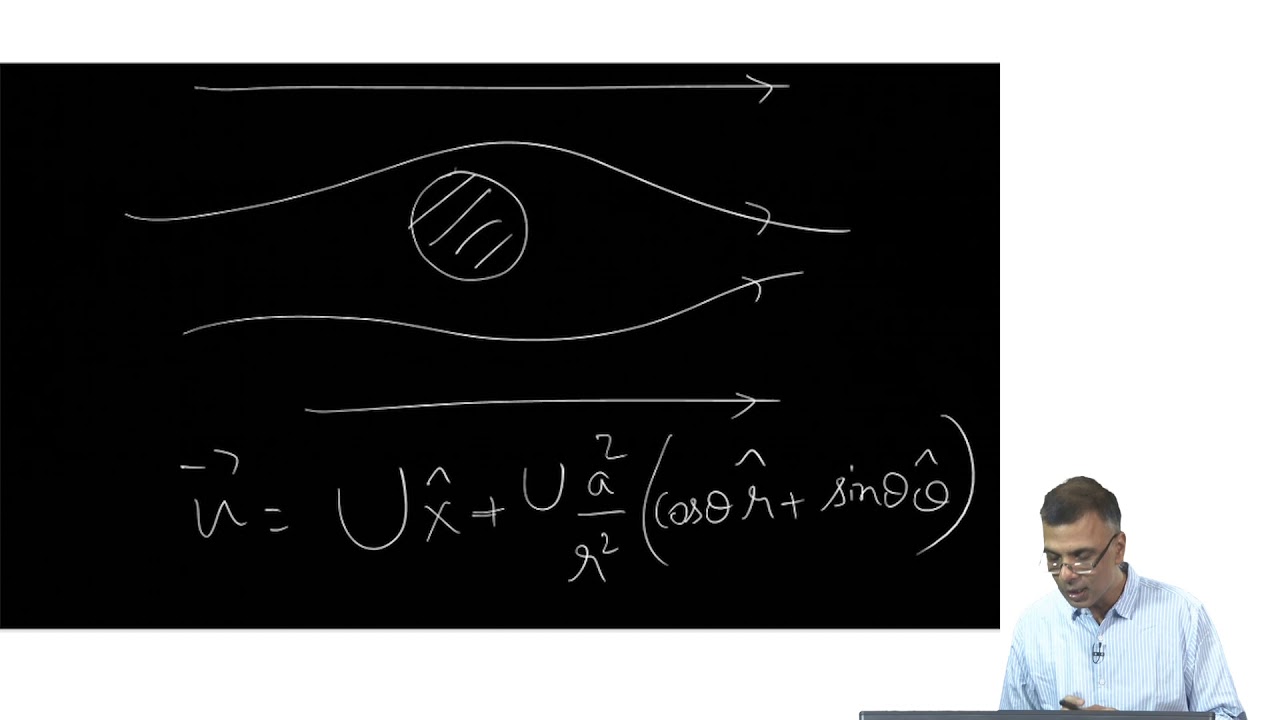
-Yes, vorticity can be present even if the flow is not visibly rotating. For example, in a straight channel flow, the fluid near the walls may experience a rotation due to viscosity, even though the overall flow appears straight.
What is the significance of Kuroko's theorem in fluid dynamics?
-Kuroko's theorem links the circulation of a fluid around a closed curve to the vorticity passing through the area enclosed by the curve. It shows how vorticity is distributed and conserved in a steady, incompressible flow with no viscous forces.
How does vorticity affect fluid flow near walls?
-In boundary layers near walls, vorticity tends to be stronger. The velocity distribution is non-uniform, causing the fluid to rotate. This effect is most pronounced near the wall and decreases as you move away from it.
What does a vorticity meter measure?
-A vorticity meter measures the angular velocity of fluid particles. It consists of two perpendicular veins that rotate based on the local vorticity of the fluid. The speed of rotation of the meter gives an indication of the vorticity present in the fluid.
What is the circulation theorem, and how does it relate to vorticity?
-The circulation theorem states that the circulation (line integral of velocity) around any closed curve in a fluid is equal to the flux of the vorticity vector through the area enclosed by the curve. This relationship helps quantify the vorticity in different regions of a flow.
How does the Coriolis force influence fluid circulation?
-The Coriolis force, due to the Earth's rotation, causes a torque on fluid particles, which affects the circulation in large-scale flows. In the Northern Hemisphere, this results in a counterclockwise rotation of fluids moving radially inward, increasing the circulation over time.
What is the connection between vorticity and lift generated by an airplane wing?
-The lift generated by an airplane wing is often explained by the concept of circulation. The higher velocity on the upper surface and lower velocity on the lower surface of the wing leads to a net circulation around the wing. This circulation generates a pressure difference, creating lift.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
5.0 / 5 (0 votes)