Modelado de Sistema Masa-Resorte-Amortiguador utilizando Laplace + Matlab Simulink
Summary
TLDREn este vídeo, el presentador explora el modelado de un sistema masa-resorte-amortiguador y cómo resolver sus ecuaciones diferenciales de segundo orden utilizando la transformada de Laplace. Se aplica una fuerza externa y se analizan las fuerzas resultantes en los componentes del sistema. El presentador deriva las ecuaciones que describen el comportamiento del sistema y destaca la importancia de esta comprensión para posibles aplicaciones de control. La simulación en Simulink ilustra cómo variaciones en los parámetros, como el coeficiente de amortiguamiento, afectan la respuesta del sistema, en particular las oscilaciones.
Takeaways
- 😀 Se continúa con el modelado de un sistema masa-resorte-amortiguador, aplicando una fuerza externa.
- 😀 La resolución de la ecuación diferencial se realizará utilizando la transformada de Laplace, un método común para ecuaciones de segundo orden.
- 😀 Al aplicar una fuerza externa, se generan fuerzas en el amortiguador, el resorte y la masa del sistema.
- 😀 Las fuerzas del sistema incluyen la fuerza del resorte, que es proporcional al desplazamiento, y la fuerza del amortiguador, que es proporcional a la velocidad.
- 😀 La relación entre la fuerza externa y las fuerzas internas se expresa en la ecuación: fuerza externa = fuerza en la masa + fuerza en el resorte + fuerza en el amortiguador.
- 😀 La transformada de Laplace se aplica a cada término de la ecuación para facilitar la resolución algebraica.
- 😀 En este análisis, se asume que el sistema parte del reposo, lo que implica que los valores iniciales son cero.
- 😀 Al aplicar la transformada de Laplace, se obtiene una función de transferencia que describe el comportamiento del sistema.
- 😀 El objetivo del modelado es entender el sistema para luego poder aplicar un control si es necesario.
- 😀 En Simulink, se simula el sistema para observar su respuesta ante la fuerza externa aplicada.
Q & A
¿Cuál es el objetivo principal del video?
-El objetivo principal del video es modelar un sistema masa-resorte-amortiguador y analizar su respuesta a una fuerza externa mediante la transformada de Laplace.
¿Qué método se utilizó anteriormente para resolver las ecuaciones del sistema?
-En un video anterior, se resolvieron las ecuaciones diferenciales utilizando Simulink.
¿Por qué se utiliza la transformada de Laplace en este contexto?
-La transformada de Laplace se utiliza porque facilita la resolución de ecuaciones diferenciales de segundo orden y superiores, que pueden ser complicadas de manejar directamente.
¿Qué fuerzas se generan al aplicar una fuerza externa al sistema?
-Al aplicar una fuerza externa, se generan fuerzas en el resorte, el amortiguador y la masa del sistema.
¿Cómo se relacionan las fuerzas en el sistema según la ecuación presentada?
-La fuerza externa es igual a la suma de las fuerzas en la masa, el resorte y el amortiguador, expresada como F_external = F_mass + F_spring + F_damper.
¿Qué significa que el sistema esté en reposo al inicio del análisis?
-Significa que los valores iniciales de las condiciones del sistema son cero, facilitando el análisis de la respuesta del sistema a partir de un estado de equilibrio.
¿Cuál es la forma final de la función de transferencia derivada en el video?
-La forma final de la función de transferencia es H(s) = F_external(s) / (m*s^2 + b*s + k), donde m es la masa, b es el coeficiente de fricción y k es la constante del resorte.
¿Cómo afecta el coeficiente de fricción al comportamiento del sistema?
-Un mayor coeficiente de fricción reduce las oscilaciones del sistema, ya que el amortiguador disipa energía en forma de calor.
¿Cuál es la importancia de modelar sistemas como el presentado?
-Modelar sistemas permite entender su comportamiento ante fuerzas externas y aplicar controles necesarios para optimizar su rendimiento.
¿Qué se espera observar al simular el sistema en Simulink?
-Se espera observar la respuesta del sistema ante una entrada de tipo escalón y cómo las variaciones en los parámetros afectan el comportamiento del sistema.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
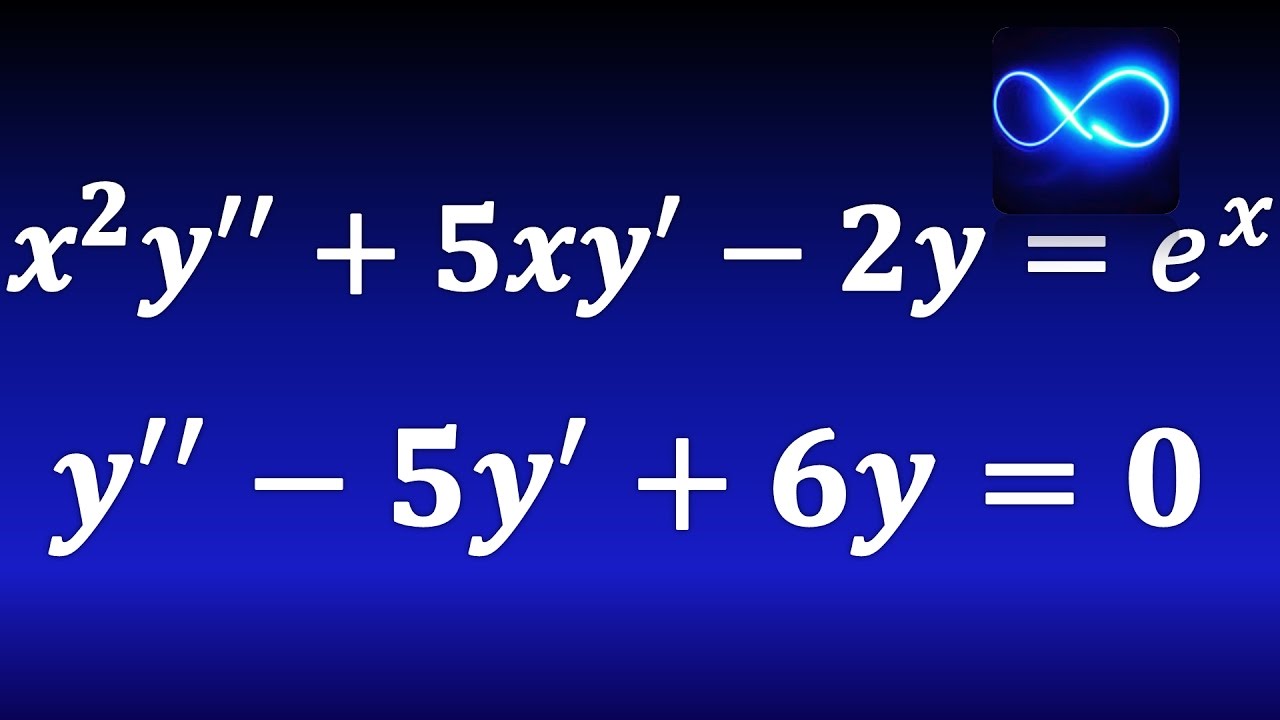
78. Qué son las ecuaciones de segundo orden, ecuaciones homogéneas y de coeficientes constantes
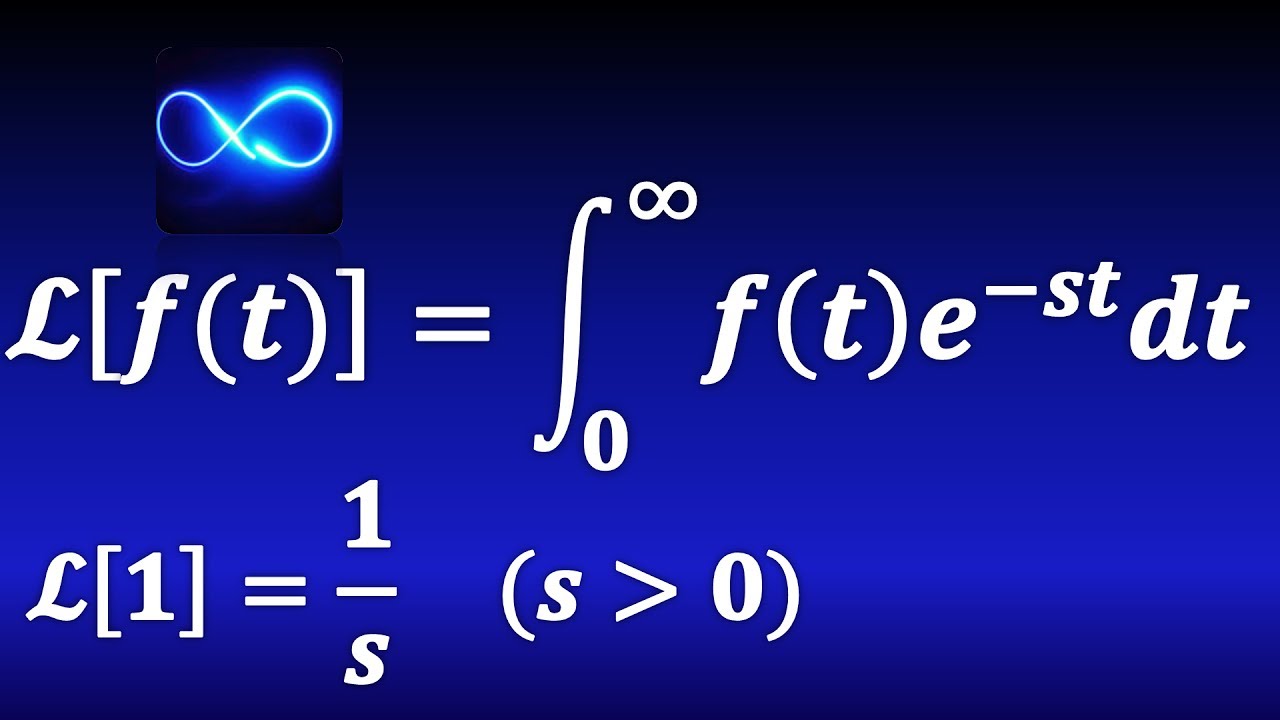
168. Transformada de Laplace: ¿qué es?. Definición, explicación y primer ejemplo.
Sistema de Suspensión Doble
Ecuaciones diferenciales con Mathematica: Apliaciones de los sistemas de ecuaciones diferen | | UPV

Laplace con matlab. Vídeo 5

Variables Separables, video 1
5.0 / 5 (0 votes)
