AMD T01 - Definición de Cuerpo y Ejemplos
Summary
TLDREn este video se explican las propiedades aritméticas básicas que se utilizan al resolver ecuaciones algebraicas. A través de la resolución de una ecuación simple, se destacan propiedades como la asociativa, conmutativa, el elemento neutro, el inverso aditivo y multiplicativo, entre otras. También se introducen los cuerpos algebraicos, conjuntos con dos operaciones que cumplen con estas propiedades. Además de los números reales, se presentan otros cuerpos como los números racionales, complejos y cuerpos finitos como Z2 y Z5, que son fundamentales en áreas como la informática y las matemáticas avanzadas.
Takeaways
- 📚 Se presentan las propiedades aritméticas básicas que se utilizan al resolver ecuaciones algebraicas.
- ➕ Al sumar 2x y 4x se obtiene 6x, un paso inicial en la resolución de la ecuación.
- 🔄 La propiedad conmutativa permite cambiar el orden de los términos al sumar.
- ➖ Para mover un término al otro lado de la ecuación, se utiliza la propiedad de existencia del opuesto (sumar el negativo de un número).
- 0️⃣ La propiedad de la existencia del cero indica que sumar cero a cualquier número no cambia su valor.
- ✖️ Se puede agrupar y factorizar términos comunes, como x en 2x + 4x.
- ➗ Para despejar x, se multiplica por el inverso de 6, que es 1/6, utilizando la propiedad de existencia del inverso.
- 🔁 La propiedad asociativa permite reordenar términos tanto en sumas como en multiplicaciones.
- 1️⃣ La propiedad del uno establece que cualquier número multiplicado por uno permanece igual.
- 🧮 Los cuerpos algebraicos, como los números reales, racionales y complejos, cumplen estas propiedades y son fundamentales para resolver ecuaciones.
Q & A
¿Cuáles son las propiedades aritméticas básicas mencionadas en el vídeo?
-Las propiedades aritméticas básicas mencionadas son: la asociatividad de la suma (propiedad 1), el cambio de orden en la suma (propiedad 2), la existencia de un elemento neutro para la suma (propiedad 3), la existencia de un opuesto para cada elemento (propiedad 4), la asociatividad de la multiplicación (propiedad 5), la distributividad de la multiplicación sobre la suma (propiedad 9), la existencia de un elemento neutro para la multiplicación (propiedad 7) y la existencia de un inverso multiplicativo para cada elemento no nulo (propiedad 8).
¿Qué es un cuerpo en matemáticas según el vídeo?
-Un cuerpo en matemáticas es un conjunto con dos operaciones, suma y producto, que cumplen con un conjunto de propiedades, como la asociatividad, la distributividad, la existencia de elementos neutros y la existencia de inversos multiplicativos para cada elemento no nulo.
¿Cuál es la ecuación que se resuelve en el vídeo?
-La ecuación que se resuelve es 2x + 4x = 10, y al despejar a x se obtiene que x = 2.
¿Cómo se demuestra la propiedad de la asociatividad de la suma en el vídeo?
-Se demuestra agrupando los términos 2x y 4x de dos maneras diferentes y mostrando que el resultado es el mismo, lo cual es consistente con la propiedad de la asociatividad de la suma.
¿Cómo se utiliza la propiedad de la distributividad de la multiplicación sobre la suma en el vídeo?
-Se utiliza al agrupar el término x en 2x y 4x, lo cual permite factorizar el x común y simplificar la ecuación.
¿Qué es el cuerpo de los números reales y cómo se denota?
-El cuerpo de los números reales es el conjunto de todos los números reales y se denota con la letra 'R'.
¿Qué es el cuerpo de los números racionales y cómo se denota?
-El cuerpo de los números racionales es el conjunto de todas las fracciones y se denota con la letra 'Q'.
¿Qué es el cuerpo de los números complejos y cómo se denota?
-El cuerpo de los números complejos es el conjunto de todos los números que pueden escribirse en la forma a + bi, donde 'a' y 'b' son números reales y 'i' es la unidad imaginaria, y se denota con la letra 'C'.
¿Qué es el cuerpo de los números enteros módulo 5 y cómo se describe en el vídeo?
-El cuerpo de los números enteros módulo 5, denotado como Z5, es el conjunto {0, 1, 2, 3, 4} con las operaciones de suma y multiplicación definidas por tablas específicas. En el vídeo se muestra cómo se resuelve una ecuación en este cuerpo usando estas tablas.
¿Cómo se determina el inverso multiplicativo de un elemento en un cuerpo no trivial como Z5?
-Se determina buscando un número que, al multiplicarse por el elemento en cuestión, dé como resultado el elemento neutro de la multiplicación en ese cuerpo. En el caso de Z5, se utiliza una tabla de multiplicación para encontrar estos inversos.
¿Cuál es la importancia de los cuerpos en la informática según el vídeo?
-Los cuerpos son fundamentales en la informática, ya que permiten realizar operaciones aritméticas en diferentes conjuntos de números, como los enteros módulo 2, que son esenciales para el funcionamiento de los sistemas binarios.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

2.3 Ecuación de primer grado con la forma (ax+b)/c=(dx+e)/f (Parte 2).

Ecuaciones de la cinemática - movimiento rectilíneo uniforme y uniformemente acelerado

Despeje de ecuaciones | Despejar una variable | Parte 2

✅PROPIEDADES de los NÚMEROS REALES | 𝙀𝙭𝙥𝙡𝙞𝙘𝙖𝙙𝙤 𝙚𝙣 10 𝙢𝙞𝙣𝙪𝙩𝙤𝙨 😎🫵💯| ARITMÉTICA

¿Qué aprenderás en el curso de ecuaciones polinómicas?
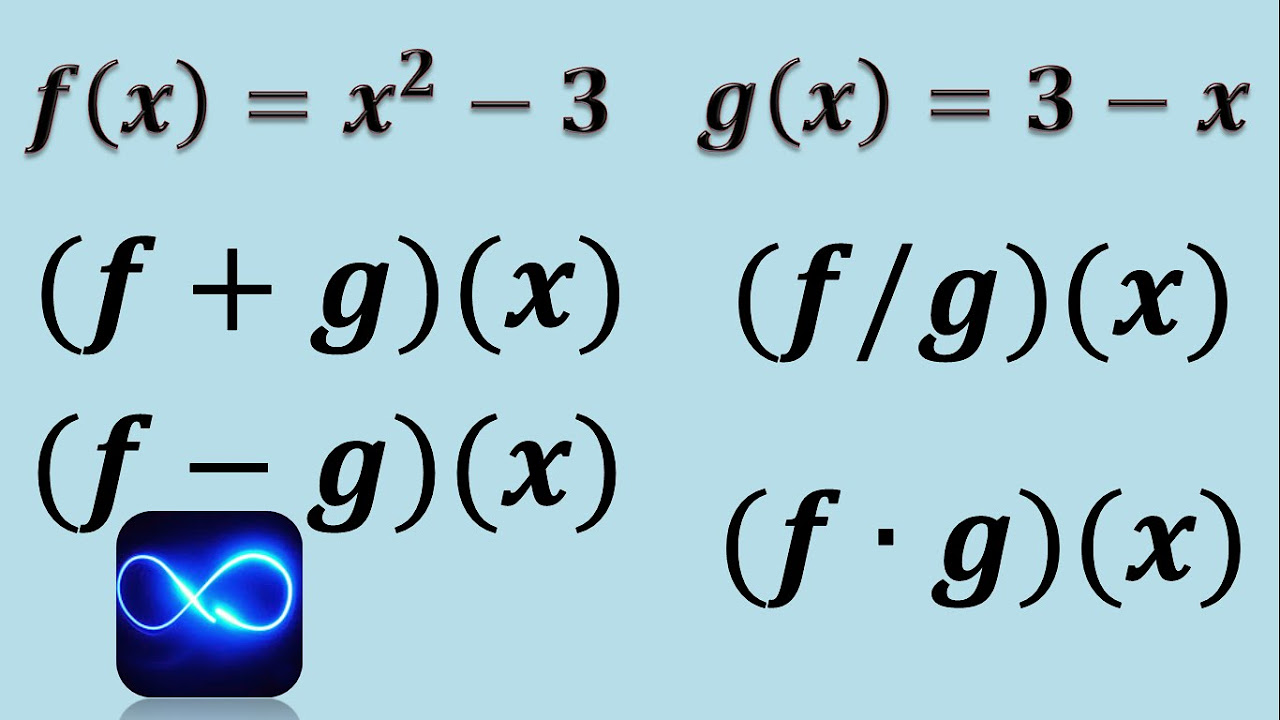
Operaciones con funciones (Suma, resta, multiplicación y división) (Ejemplo 2)
5.0 / 5 (0 votes)
