Tips Mudah Menyederhanakan Bentuk Akar || Bab Bilangan Berpangkat (Part 2)

Summary

This video tutorial focuses on simplifying square roots, a fundamental concept in mathematics. The presenter explains the basics of square roots, their relationship with exponents, and key properties. They cover the difference between rational and irrational numbers, providing examples like √2 and √9. The video also teaches how to simplify square roots using familiar square numbers and explains the process step-by-step. It concludes by offering practice problems for viewers and promises a future video on operations involving square roots, such as addition, subtraction, multiplication, division, and rationalizing denominators.

Takeaways

• 🔢 Simplifying square roots is a fundamental concept, and many students find it confusing.
• 📚 The lesson is part of a broader topic covering exponents and square roots, starting with understanding square roots.
• 🌳 In mathematics, square roots are not related to trees but represent the root of a rational number, often resulting in an irrational number.
• ✖️ A square root produces a rational number when it is a perfect square (e.g., √4 = 2, √9 = 3), but non-perfect squares (e.g., √2) result in irrational numbers.
• 🔢 Irrational numbers cannot be expressed as simple fractions, and their decimal expansions are non-terminating and non-repeating.
• ⚖️ There is a connection between square roots and fractional exponents, where a root can be rewritten as a fractional exponent (e.g., √8 = 8^(1/2)).
• 💡 Square root properties: The square of a square root returns the original number (e.g., (√3)^2 = 3).
• ✖️ Multiplying and dividing square roots follows specific rules (e.g., √4 * √9 = √36 = 6).
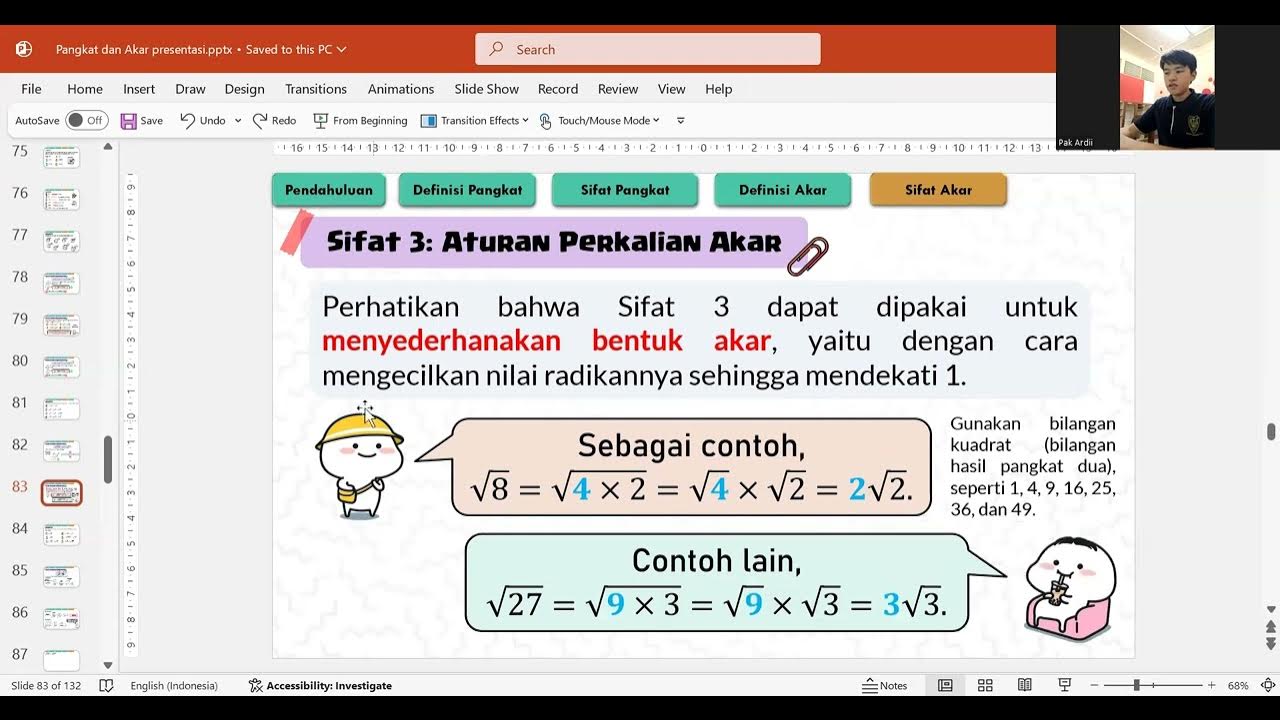
• 🧮 Simplifying square roots involves breaking numbers into factors that include perfect squares (e.g., √8 = √4 * √2 = 2√2).
• 🔄 It is easier to simplify square roots using the largest possible perfect square factor.

Q & A

What is the primary focus of the video?

The video focuses on simplifying square roots, a fundamental topic in mathematics, particularly in relation to exponentiation and square roots. It aims to clarify basic concepts that some students may find confusing.

How is a square root defined in mathematics, according to the video?

In mathematics, a square root is the inverse operation of squaring a number. It refers to finding a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because 3² equals 9.

What is the difference between rational and irrational numbers, as discussed in the video?

Rational numbers can be expressed as fractions of two integers (a/b), while irrational numbers cannot. Irrational numbers, like √2, have decimal expansions that go on infinitely without a repeating pattern.

Can you give examples of numbers that are not considered square roots?

Numbers like √4, √9, and √16 are not considered in the context of square roots discussed in the video because they result in rational numbers (2, 3, and 4 respectively). The focus is on irrational roots like √2, √3, and √5.

What is the relationship between exponents and square roots?

Square roots can be expressed as fractional exponents. For instance, the square root of a number can be written as that number raised to the power of 1/2. This is a different way of representing the same operation.

What is an important property of square roots mentioned in the video?

One important property is that the square root of a number squared results in the original number. For example, √(3²) equals 3.

How can square roots be simplified using their properties?

Square roots can be simplified by factoring the number under the root into its prime factors and separating out the perfect squares. For instance, √8 can be simplified to 2√2 because 8 = 4 * 2, and √4 equals 2.

Why is understanding perfect squares important for simplifying square roots?

Knowing perfect squares helps in simplifying square roots by identifying factors that can be easily extracted from under the square root. For example, √50 simplifies to 5√2 because 50 = 25 * 2, and √25 equals 5.

What is a key tip provided in the video for simplifying square roots more efficiently?

A key tip is to always look for the largest perfect square factor when simplifying square roots. This reduces the number of steps needed and avoids unnecessary complexity.

What will be discussed in the next video, according to the script?

The next video will cover operations involving square roots, including addition, subtraction, multiplication, division, and rationalizing square roots.