Introducción a la robótica: Posición, orientación y tramas
Summary
TLDRThis video script delves into the fundamentals of robotics, focusing on the description of a point's position and orientation in space with respect to a coordinate system. The master explains the use of position vectors and rotation matrices to define a robot's arm orientation, emphasizing the importance of accurately representing both position and orientation. The concept of a 'transform', a set of four vectors encompassing position and orientation data, is introduced. The script also touches on the application of these principles in robotic arms, highlighting the kinematic chain's representation through coordinate systems and the practicality of using transforms for various robotic systems.
Takeaways
- 📍 The script introduces the concept of describing a point's position in space with reference to a coordinate system, specifically the A and Y coordinate system.
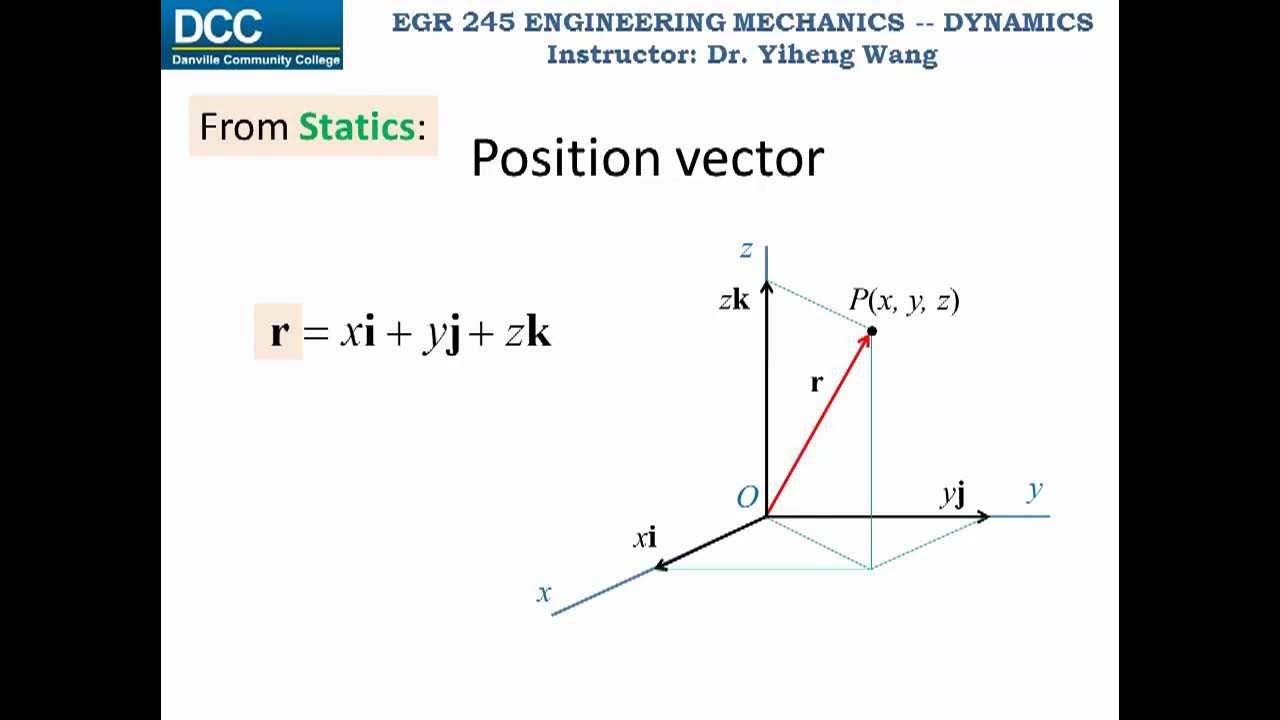
- 🔄 The point P can be represented by coordinates (x, y, z) in a right-handed coordinated system, with the superscript 'a' indicating reference to the A coordinate system.
- 🚦 The description of orientation is more complex than position and requires not one but three vectors to fully describe the orientation of a robotic arm or end effector.
- 📊 A 3x3 matrix, represented by 'R', is used to describe the orientation, which is essentially a rotation matrix from system A to system B.
- 🔢 The elements of the rotation matrix R are the projections of the principal vectors of system B onto the elements of system A, calculated using dot product and trigonometric functions.
- ⏬ The script explains that the rotation matrix R can also be represented as the transpose of matrix R, when analyzed by rows instead of columns.
- 🔍 By analyzing the rotation matrix by columns and rows, insights into the projections of the system B's vectors onto system A's vectors are gained.
- 💠 The term 'transform' (trama in Spanish) is introduced as a set of four vectors providing information about position and orientation, consisting of a 3x3 rotation matrix and a position vector.
- 🔄 The transform allows representing any coordinate system relative to a previous or 'base' coordinate system, which is crucial in robotics for representing the kinematic chains of an articulated robotic arm.
- 📈 The script concludes by emphasizing the practical application of transforms in robotics, particularly in understanding the relationship between different coordinate systems in the context of a robotic arm.
Q & A
What is the main topic of the video?
-The main topic of the video is the description of the position and orientation of a point in space with reference to a coordinate system, specifically focusing on robotics.
How is a point represented in a coordinate system?
-A point is represented by its coordinates with respect to a given coordinate system. In the video, the point P is represented by its coordinates (x, y, z) in the A coordinate system.
What are the three axes of a right-handed coordinate system mentioned in the video?
-The three axes of a right-handed coordinate system mentioned are the x, y, and z axes.
Why is it necessary to describe the orientation in robotics?
-Describing the orientation is necessary in robotics because a robotic arm or end effector can be rotated in any direction while keeping a point stationary, and this rotation needs to be accounted for in addition to the position.
How many vectors are required to fully describe the orientation of a system?
-Three vectors are required to fully describe the orientation of a system, which together form a 3x3 matrix.
What does the 3x3 matrix represent in the context of the video?
-The 3x3 matrix represents a rotation matrix, which describes the orientation of one coordinate system (B) with respect to another (A). It is a mathematical representation of how the basis vectors of one system are projected onto the other system.
How is the rotation matrix (R) related to the transpose of the matrix?
-The rotation matrix (R) is the transpose of the matrix because when analyzed by rows instead of columns, it represents the projection of the basis vectors of one system onto the other, thus giving the orientation of one system with respect to the other.
What is a transformation matrix (or 'trama' in Spanish) in robotics?
-A transformation matrix, or 'trama', is a set of four vectors that provide information about both the position and orientation of a coordinate system. It consists of a 3x3 rotation matrix and a position vector.
How many coordinate systems can be represented in relation to the initial system?
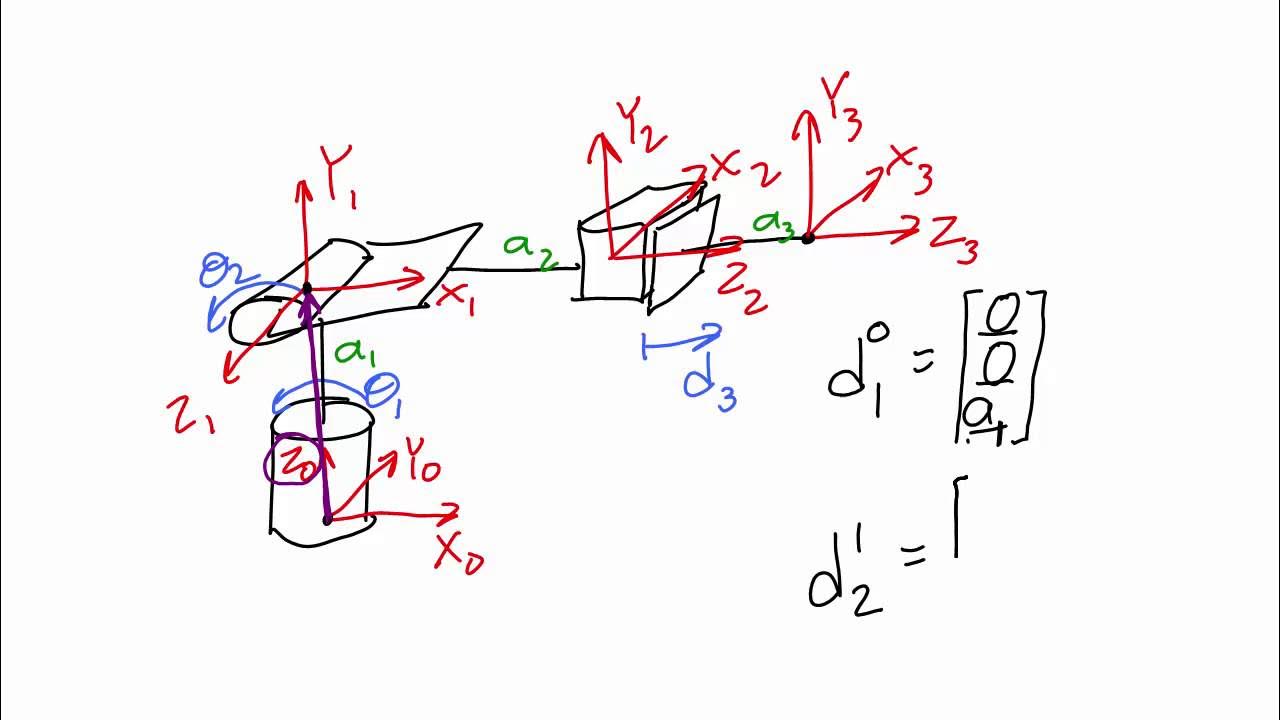
-Multiple coordinate systems can be represented in relation to the initial system. Each subsequent system can be described with respect to the previous one, forming a chain of transformations.
What does the base system (system U) represent in the context of a robotic arm?
-In the context of a robotic arm, the base system (system U) represents the fixed part of the arm where the coordinate system origin is placed, and it is the reference point for the rest of the moving segments in the robotic chain.
How are the transformation matrices used in the kinematic chain of a robotic arm?
-Transformation matrices are used to represent the position and orientation of each link in the kinematic chain of a robotic arm with respect to the previous link. They help in calculating the overall position and orientation of the end effector.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

Lecture 15: Robot Kinematics (Contd.)
Dynamics Lecture 02: Particle kinematics, Rectilinear continuous motion part 1
What is the Cartesian Coordinate System? | Don't Memorise

Lec 12 - Rectangular Coordinate System
The ROS Transform System (TF) | Getting Ready to Build Robots with ROS #6
1 1 4 Lecture Video 1 of 2 Displacement Vectors
5.0 / 5 (0 votes)
