Lec 12 - Rectangular Coordinate System
Summary
TLDRThis video introduces the fundamentals of coordinate geometry, focusing on the rectangular coordinate system and its key elements: axes, points, and lines. The system uses the x-axis and y-axis to define the location of points on a plane, expressed as coordinates (x, y). The plane is divided into four quadrants based on the signs of these coordinates, which helps in categorizing points. The lesson emphasizes understanding how to plot points, analyze their positions, and work within these quadrants to graph functions and geometric shapes effectively.
Takeaways
- 😀 **Rectangular Coordinate System**: The coordinate system consists of two perpendicular axes – the **X-axis** (horizontal) and **Y-axis** (vertical) – which intersect at the **origin** (0,0).
- 😀 **Coordinates**: Any point on the coordinate plane is represented by a pair of values (x, y), where x is the distance along the X-axis and y is the distance along the Y-axis.
- 😀 **Positive and Negative Axes**: The X-axis has both positive and negative parts, and similarly, the Y-axis has positive and negative parts. Positive X is to the right, and positive Y is upwards.
- 😀 **Plotting Points**: To plot a point, move along the X-axis for the x-coordinate and along the Y-axis for the y-coordinate. For example, (3, 4) means 3 units right and 4 units up.
- 😀 **Quadrants**: The coordinate plane is divided into four quadrants: Quadrant I (positive x, positive y), Quadrant II (negative x, positive y), Quadrant III (negative x, negative y), and Quadrant IV (positive x, negative y).
- 😀 **Origin**: The point where the X-axis and Y-axis meet is called the **origin**, and its coordinates are (0, 0).
- 😀 **Special Points on Axes**: Points that lie on the X-axis have a y-coordinate of 0, and points on the Y-axis have an x-coordinate of 0. For example, (5, 0) is on the X-axis and (0, 5) is on the Y-axis.
- 😀 **Axes Dividing the Plane**: The X-axis and Y-axis divide the plane into four quadrants and two axes, helping us identify the location of points quickly.
- 😀 **Understanding Parity in Quadrants**: In **odd quadrants** (I and III), the x and y coordinates share the same sign, while in **even quadrants** (II and IV), the x and y coordinates have opposite signs.
- 😀 **Application of Quadrants**: Knowing the quadrants helps in graphing and understanding the relative positions of points, enabling a more efficient approach to graphing and analyzing functions.
- 😀 **Precision of Coordinates**: Coordinates provide a precise way to describe the location of a point on a plane, such as specifying how far to move horizontally (x) and vertically (y) from the origin.
Q & A
What is the main purpose of the Rectangular Coordinate System?
-The main purpose of the Rectangular Coordinate System is to provide a way to precisely describe the location of points in a plane using numerical coordinates based on two perpendicular axes: the X-axis and Y-axis.
How do you describe the position of a point on a coordinate plane without the coordinate system?
-Without a coordinate system, the position of a point can only be described vaguely, such as 'slightly to the right and up.' This is not precise, and a numerical system is needed to give the exact location of the point.
What are the X-axis and Y-axis, and how do they relate to the coordinate plane?
-The X-axis is the horizontal axis, and the Y-axis is the vertical axis in the coordinate plane. The two axes intersect at the origin, dividing the plane into four quadrants and providing a reference for specifying the position of points using coordinates (x, y).
What is the origin, and what are its coordinates?
-The origin is the point where the X-axis and Y-axis intersect. Its coordinates are (0, 0), which means it is at zero units along both the horizontal and vertical axes.
How do you plot a point using coordinates?
-To plot a point with coordinates (x, y), you move 'x' units horizontally (right for positive, left for negative) and 'y' units vertically (up for positive, down for negative) from the origin. For example, the point (3, 4) is plotted by moving 3 units to the right and 4 units up.
What are the four quadrants of the coordinate plane?
-The coordinate plane is divided into four quadrants: Quadrant I (positive x and y values), Quadrant II (negative x and positive y values), Quadrant III (negative x and y values), and Quadrant IV (positive x and negative y values).
What is the significance of the quadrants in graphing points?
-The quadrants help classify the points based on their x and y values, making it easier to analyze and graph data. Points in each quadrant have distinct sign combinations for their coordinates, which can be useful when plotting functions or analyzing geometric relationships.
What happens if a point lies on one of the axes?
-If a point lies on one of the axes, it does not belong to any quadrant. For example, the point (5, 0) lies on the X-axis, and the point (0, 5) lies on the Y-axis.
How can understanding the quadrants improve graphing functions?
-Understanding the quadrants allows you to focus on specific areas of the coordinate plane when graphing functions. For example, if most of your points lie in Quadrant I, you can scale and adjust your graphing range to zoom in on that quadrant for more accurate representation.
Why are odd quadrants (I and III) said to have the same parity for coordinates?
-Odd quadrants (I and III) have the same parity because both x and y coordinates either have the same sign (both positive in Quadrant I, both negative in Quadrant III), while even quadrants (II and IV) have opposite signs for the coordinates.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

SSLC Maths | Coordinates സൂചകസംഖ്യകൾ | Full Chapter in 19 Minutes | Must Watch | Exam Winner
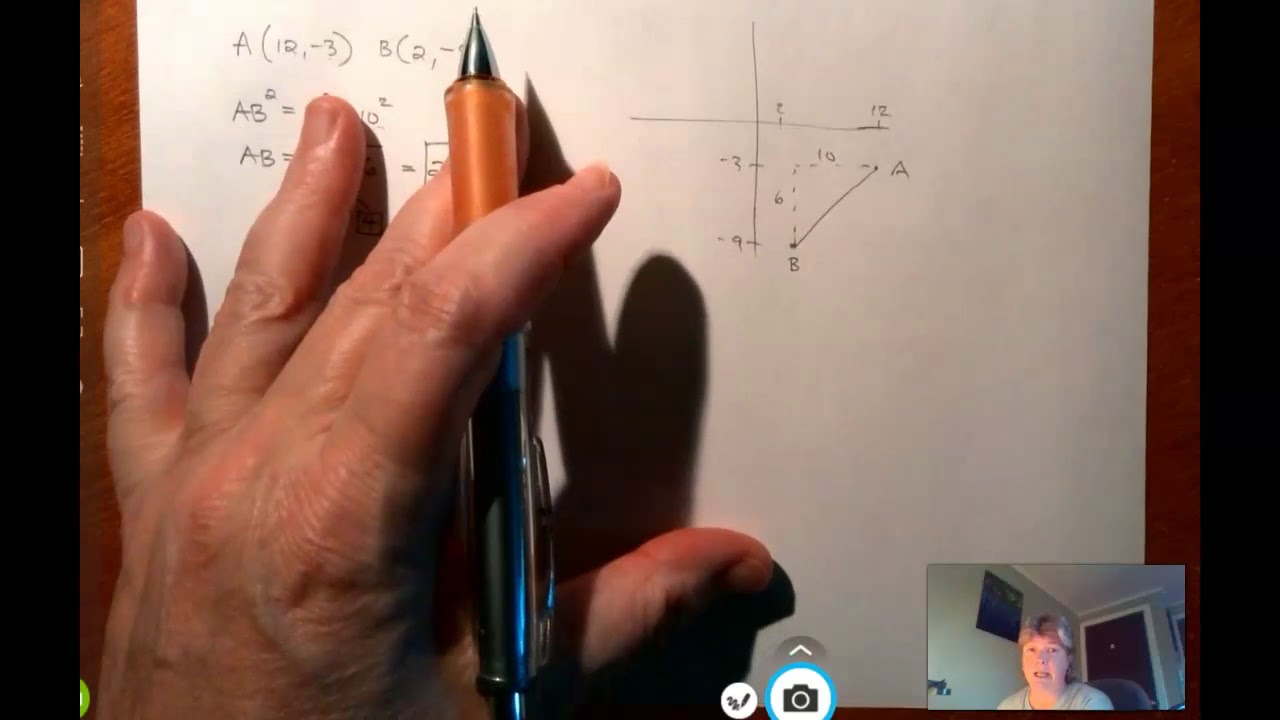
Distance and Midpoint

The Rectangular Coordinate System / Cartesian Plane

Coordinate Geometry Class 10 ICSE | Section Formula | Mid Point Formula | Sir Tarun Rupani

Grade 8 Math Q1 Ep9: Rectangular Coordinate System

Coordinate Geometry Class 9 in 12 Minutes 🔥 | Class 9 Maths Chapter 3 Complete Lecture
5.0 / 5 (0 votes)