Límites por racionalización 1

BRO Clases profe Bryan

8 May 202410:52

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.

Посмотреть больше похожих видео

Solución de límites por racionalización | Ejemplo 2

Limites algebraicos | expresiones con raíces | Cálculo diferencial

Solución de límites por factorización | Introducción

⛔️ Cómo calcular LIMITES LATERALES FUNCIÓN POR PARTES - FUNCIÓN A TROZOS| Juliana la profe

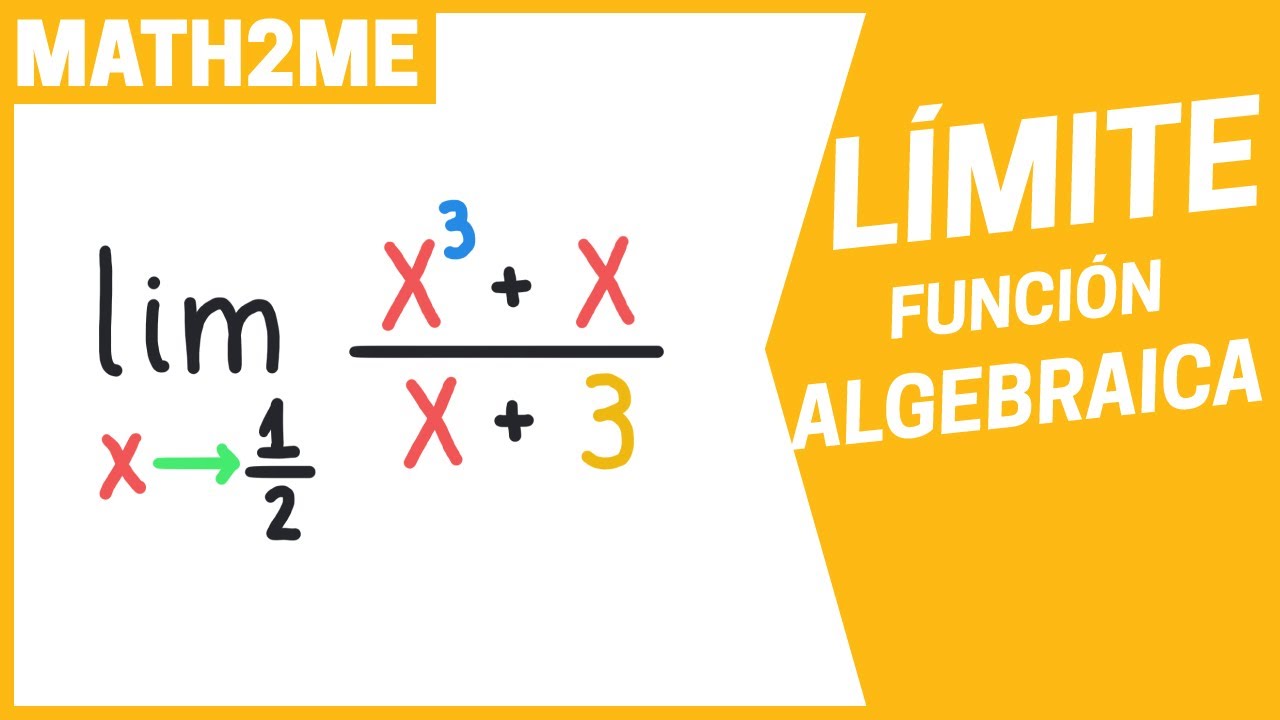
LÍMITE de una función algebraica - ejercicio

Qué es un Límite

Rate This

★

5.0 / 5 (0 votes)