3.4 Signal Conditioning for Resistive Sensors - Wheatstone Bridge
Summary
TLDRThe video script discusses the Wheatstone bridge, a circuit with two voltage dividers, to convert strain gage resistance changes into a measurable voltage. It explains how the bridge can amplify small signals and reduce the impact of source impedance. The script also covers using strain gauges in the bridge to account for temperature effects and increase measurement sensitivity, ensuring accurate and linear outputs.
Takeaways
- 🔌 A Wheatstone bridge is a circuit with two voltage dividers that can convert changes in resistance into a voltage signal.
- 📉 The Wheatstone bridge outputs the difference between the voltages of its two voltage dividers, which can amplify small signals.
- ⚖️ A balanced Wheatstone bridge, where the resistor ratios are equal, has an output voltage of zero.
- 🔍 The bridge can be used to measure changes in resistance from a strain gauge by substituting one of the resistors with the gauge.
- 📊 The output voltage of the bridge is proportional to the change in resistance (X) divided by the ratio of the resistors (K) plus one.
- 🌡️ Strain gauges can have a temperature-dependent resistance change, which can be accounted for by including another strain gauge in the bridge.
- 🔄 Placing strain gauges on opposite surfaces of a material can help cancel out temperature effects, as their resistance changes will have opposite signs.
- 🔬 Using four strain gauges in the Wheatstone bridge increases sensitivity and can potentially cancel out temperature effects without assumptions.
- 🔄 The output of the Wheatstone bridge is linear when using strain gauges on opposite surfaces, eliminating the need for linearity assumptions.
- 🔬 The script suggests that it would be an exercise to explore if temperature dependence cancels out when all resistors in the bridge are strain gauges.
Q & A
What is a Wheatstone bridge?
-A Wheatstone bridge is an electrical circuit that consists of two voltage dividers connected to a common node. It is used to measure an unknown resistance by balancing the bridge, which results in a null output voltage. The bridge consists of four resistors, typically labeled R1, R2, R3, and R4.
How does a Wheatstone bridge solve the problem of a small signal riding on a large fixed signal?
-A Wheatstone bridge solves this problem by taking the difference between the voltages of the two voltage dividers. When the bridge is balanced, the output voltage is zero, effectively eliminating the large fixed signal and amplifying the small signal of interest.
What is the formula for the output voltage of a Wheatstone bridge?
-The output voltage (V_out) of a Wheatstone bridge is given by the formula V_out = (R4/(R3 + R4) * V) - (R2/(R1 + R2) * V), where V is the supply voltage and R1, R2, R3, and R4 are the resistances in the bridge.
How does a Wheatstone bridge convert the change in resistance of a strain gauge into a voltage?
-By substituting a strain gauge for one of the resistors in the bridge, such as R4, the change in resistance due to strain can be converted into a voltage change at the output of the bridge. The output voltage is then proportional to the change in resistance of the strain gauge.
What is the effect of temperature on a strain gauge?
-Temperature can cause an additional change in the resistance of a strain gauge, represented as (1 + y), where y is the fractional change in resistance due to temperature.
How can the Wheatstone bridge be used to cancel out the temperature effect on a strain gauge?
-By placing strain gauges in two opposite positions of the bridge, one experiencing strain and the other not, the temperature-induced resistance changes will be of the same magnitude but opposite in sign, thus canceling each other out in the bridge's output.
What is the advantage of using four strain gauges in a Wheatstone bridge?
-Using four strain gauges increases the sensitivity of the measurement. Each gauge can measure changes in resistance due to strain, and if they are all in the same environment, they can also cancel out temperature effects.
What is the significance of the assumption that X is much smaller than 1 + K in the context of the Wheatstone bridge?
-This assumption simplifies the output equation of the Wheatstone bridge, allowing the fixed voltage term to cancel out, resulting in an output voltage that is solely dependent on the change in resistance (X), which is the desired measurement.
How does connecting a strain gauge to the opposite surface of the first strain gauge help in obtaining a linear output?
-When strain gauges are connected to opposite surfaces, the resistance changes due to strain have opposite signs. This configuration results in a linear output from the Wheatstone bridge without needing any assumptions, as the strain-induced changes are directly proportional to the output voltage.
What is the purpose of connecting strain gauges to both the top and bottom surfaces of a material?
-Connecting strain gauges to both surfaces allows for the measurement of strain in both directions, which can be useful in applications where bidirectional strain measurement is required, such as in materials testing or structural health monitoring.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
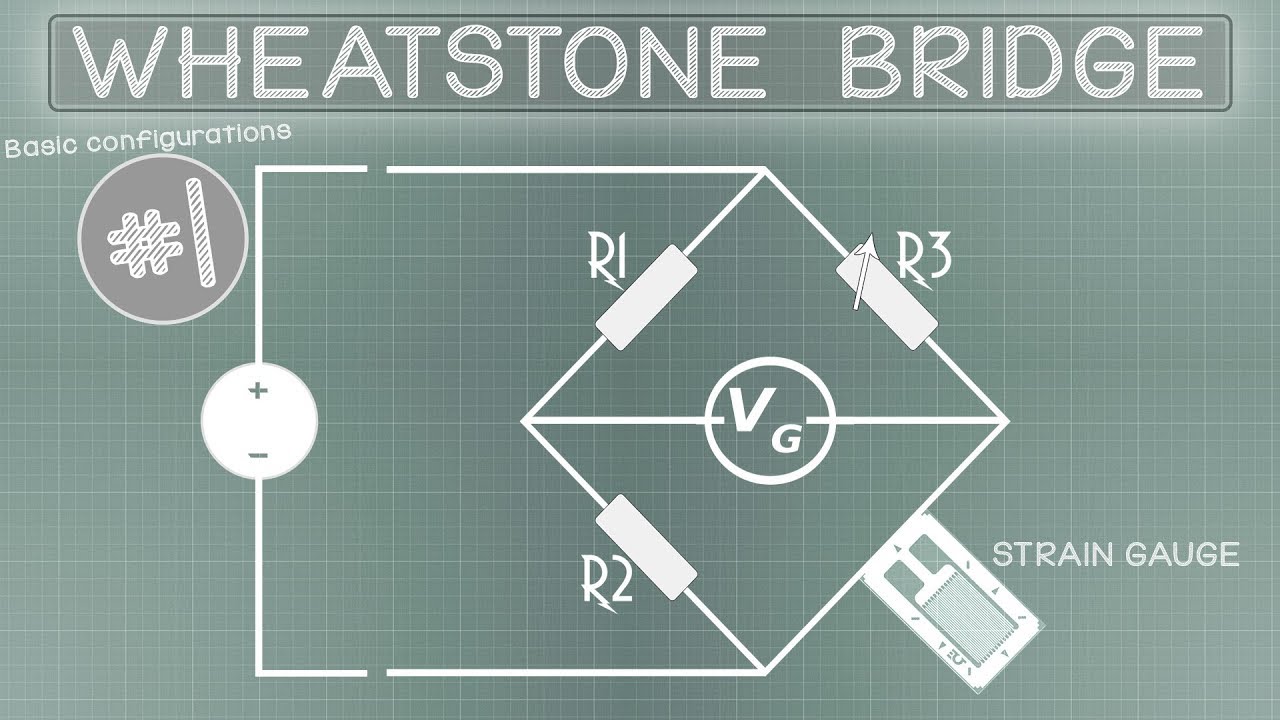
Basic configurations #1 - Wheatstone bridge
Practice circuit: making a Wheatstone bridge in TinkerCAD
How to test a load cell

How To Solve The Wheatstone Bridge Circuit
Electrical Engineering: Basic Laws (13 of 31) Series Resistors and Voltage Division
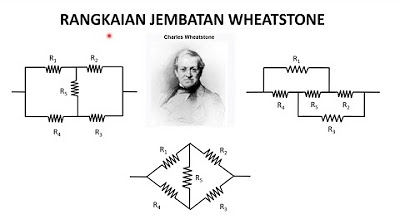
Rangkaian Jembatan Wheatstone dan Rangkaian Delta Star
5.0 / 5 (0 votes)
