U Statistics
Summary
Please replace the link and try again.
Please replace the link and try again.
Q & A
Что такое симметричное ядро, описанное в тексте?
-Симметричное ядро — это функция, которая определяется как разница между двумя значениями, возведенная в квадрат и деленная на 2: H(X1, X2) = (X1 - X2)^2 / 2. Оно симметрично, так как порядок значений X1 и X2 не влияет на результат.
Почему в расчете симметричного ядра не важен порядок значений X1 и X2?
-Порядок значений X1 и X2 не имеет значения, потому что ядро определяется как разница между ними в квадрате, и это всегда одинаково независимо от порядка значений.
Как симметричное ядро используется для оценки дисперсии?
-Для оценки дисперсии используется симметричное ядро, которое применяется к парам значений из выборки. Все такие пары обрабатываются для вычисления среднего значения ядра, которое служит оценкой дисперсии выборки.
Что такое несмещенная оценка дисперсии и как она связана с симметричным ядром?
-Несмещенная оценка дисперсии — это такая оценка, которая в среднем совпадает с истинным значением дисперсии. В данном случае, используя симметричное ядро, получается несмещенная оценка, которая равна выборочной дисперсии s^2.
Как вычисляется среднее значение для симметричного ядра по всем парам значений из выборки?
-Для всех возможных пар значений из выборки (всего nC2 пар) вычисляется значение ядра, затем эти значения усредняются, чтобы получить статистику, которая будет оценкой дисперсии.
Что такое выборочная дисперсия и как она используется в статистике?
-Выборочная дисперсия s^2 — это мера разброса значений в выборке. Она используется для оценки истинной дисперсии в генеральной совокупности, и она является несмещенной оценкой для σ^2.
Каковы основные шаги для вычисления статистики на основе симметричного ядра?
-1. Выбираются все возможные пары значений из выборки. 2. Для каждой пары вычисляется значение симметричного ядра. 3. Усредняются все эти значения, чтобы получить статистику, которая будет оценкой дисперсии.
Что означает термин 'несмещенная оценка' в контексте статистики?
-Несмещенная оценка — это такая оценка, которая, в среднем, не завышает и не занижает истинное значение параметра. В данном случае, выборочная дисперсия является несмещенной оценкой для дисперсии генеральной совокупности.
Почему важно использовать симметричное ядро для оценки дисперсии?
-Использование симметричного ядра позволяет учитывать только разницу между значениями, что делает оценку дисперсии более точной и независимой от порядка значений в паре.
Какая роль статистики в вычислении оценок параметров, таких как дисперсия?
-Статистика используется для оценки параметров генеральной совокупности, таких как дисперсия. С помощью статистических методов, таких как использование симметричного ядра, можно получить точные и несмещенные оценки параметров, что важно для анализа данных.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

2023A Kelompok 5 Statistik Non Parametrik

Statistika Parametrik atau Nonparametrik? || Memilih jenis uji dan syarat uji parametrik

Apresiasi Usai Timnas Juara Piala AFF U-19 2024 - iNews Pagi 01/08
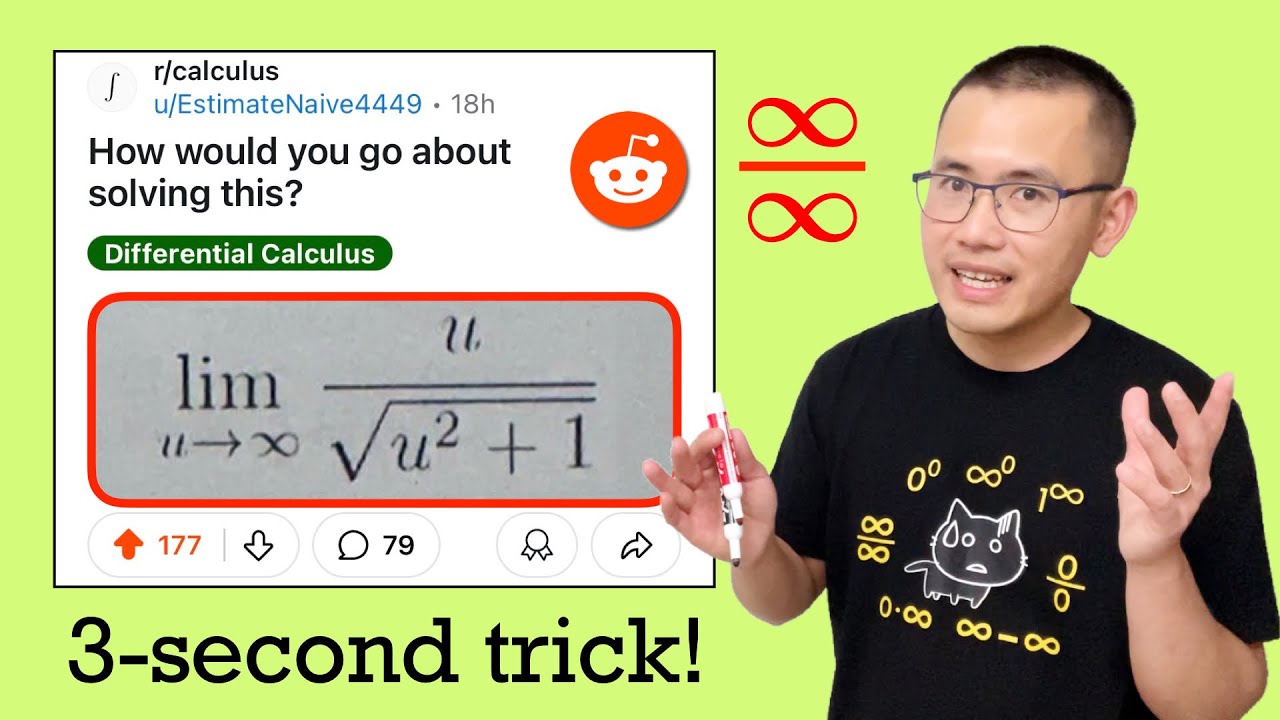
How would you go about solving this? Limit of x/sqrt(x^2+1) as x goes to infinity. Reddit inf/inf

Embedded Linux | Introduction To U-Boot | Beginners

How to Diagnose and Replace Universal Joints (ULTIMATE Guide)
5.0 / 5 (0 votes)