Suma de Riemann, paso a paso, MUY FÁCIL
Summary
TLDREn este video, se enseña a calcular una integral definida utilizando sumas de Riemann. El ejemplo se centra en la integral de una función cuadrática, resolviendo paso a paso con explicaciones detalladas sobre cómo identificar los límites, calcular Delta X, y aplicar la fórmula de suma de Riemann. El proceso incluye el desarrollo algebraico y la utilización de propiedades de sumas y límites. Al final, se simplifica la expresión obtenida y se muestra el cálculo del valor de la integral. El video concluye invitando a los espectadores a practicar con un nuevo ejercicio y a suscribirse al canal.
Takeaways
- 📚 En este video, se explica cómo calcular una integral mediante una suma de Riemann.
- ✏️ La integral que se calcula es de -1 a 3 de la función x² + 6x + 3x.
- 🔢 El proceso comienza identificando los límites de integración, con 'a' como -1 y 'b' como 3.
- 🧮 Se utiliza la fórmula de suma de Riemann y se explica cómo calcular el valor de Δx.
- 🔄 Para calcular la función evaluada, se sustituyen los valores de 'a' y 'b' en la función dada.
- 📐 Se detallan los pasos algebraicos para elevar al cuadrado términos y simplificar expresiones.
- 📝 Se utilizan fórmulas de sumas como la suma de k² y la suma gaussiana para resolver las sumas parciales.
- 🔍 Se aplican propiedades de límites al final para calcular el valor exacto de la integral.
- ✅ El resultado final de la integral es 136/3, calculado paso a paso con una suma de Riemann.
- 📹 El video concluye invitando a los espectadores a practicar con una integral diferente y a dejar comentarios o preguntas.
Q & A
¿Qué método se utiliza en el vídeo para calcular la integral?
-Se utiliza el método de la suma de Riemann para calcular la integral.
¿Cuál es la función f(x) que se integra en el vídeo?
-La función f(x) que se integra es x^2 + 6x + 3.
¿Cuál es el intervalo de integración mencionado en el vídeo?
-El intervalo de integración es de -1 a 3.
¿Cómo se calcula Δx en el método de la suma de Riemann?
-Δx se calcula como (b - a) / n, donde a es el límite inferior, b es el límite superior y n es el número de subintervalos.
¿Cómo se evalúa f(x) en el punto medio de cada subintervalo?
-Se evalúa f(x) en el punto medio de cada subintervalo sustituyendo x por (a + (kΔx)), donde k es el índice del subintervalo.
¿Cuál es la fórmula para el cuadrado de un binomio (a + b)^2?
-La fórmula para el cuadrado de un binomio es a^2 + 2ab + b^2.
¿Cómo se calculan las sumas de los términos independientes en la suma de Riemann?
-Se suman directamente los términos que no dependen de la variable de suma, como los coeficientes constantes.
¿Qué propiedades de las sumas se aplican para simplificar la expresión antes de calcular el límite?
-Se aplican propiedades de las sumas para separar y simplificar términos, extraer factores comunes y aplicar fórmulas de suma de series conocidas.
¿Cómo se calcula el límite cuando n tiende a infinito en la suma de Riemann?
-Se calcula el límite de cada término de la suma por separado y se aplican propiedades de límites, como extraer constantes y dividir por la máxima potencia de n.
¿Cuál es el resultado final de la integral calculada mediante la suma de Riemann en el vídeo?
-El resultado final de la integral es 136/3, que se obtiene al calcular el límite de la suma de Riemann cuando n tiende a infinito.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

Resolver una Suma de Riemann paso a paso. #MateYisus

MÉTODO DE ARQUÍMEDES PARA CALCULAR EL ÁREA DE UNA CIRCUNFERENCIA
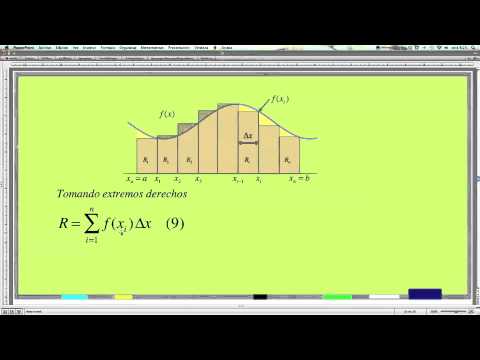
Calculo Integral 04: La integral definida. The definite integral.

Reescribir una integral definida como el límite de una suma de Riemann | Khan Academy en Español
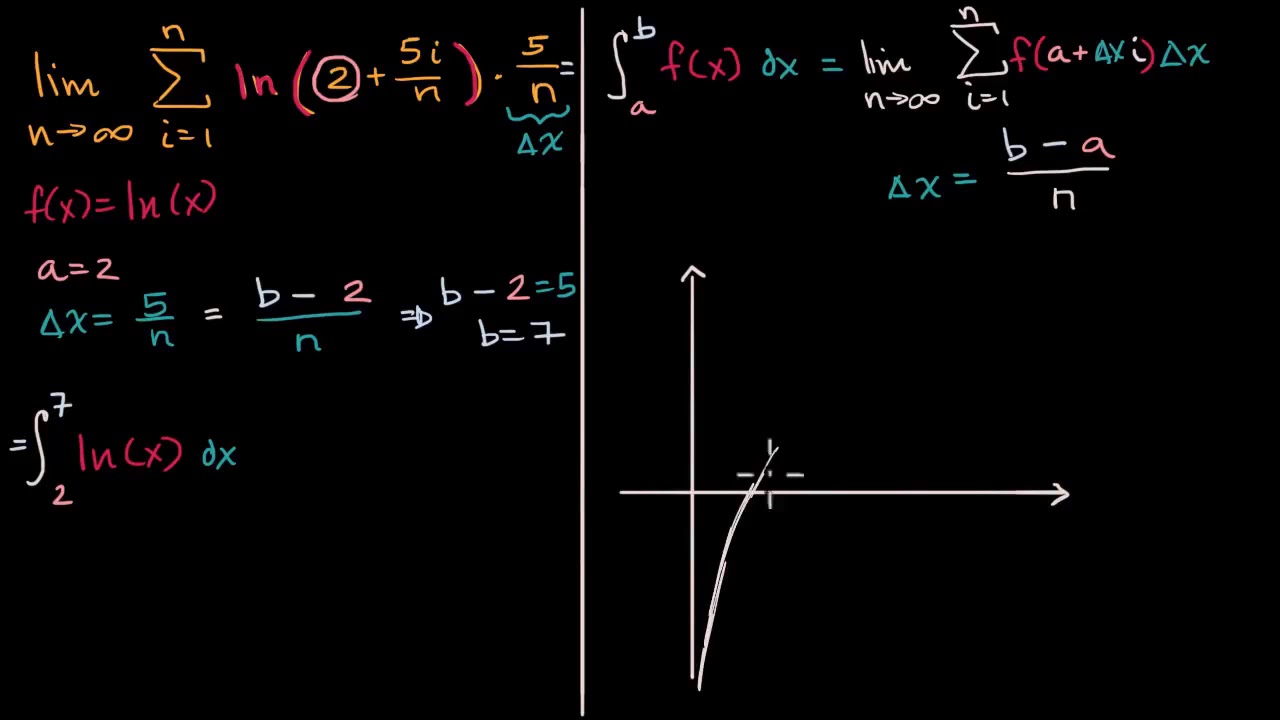
Escribir el límite de una suma de Riemann como una integral definida | Khan Academy en Español

Sumas de Riemann - Ej.1 (Paso a paso | Cuadrática)
5.0 / 5 (0 votes)
