09. ¿Qué es un sistema de ecuaciones lineales con dos incógnitas?
Summary
TLDREn este video, se explora el método gráfico para resolver sistemas de ecuaciones lineales de 2x2, que involucran dos incógnitas. Se presentan dos situaciones: una sobre la relación de edad entre una madre y su hijo, y otra sobre la compra de aguacates y jitomates a diferentes precios. El video explica las características de un sistema de ecuaciones lineales, como tener al menos dos ecuaciones relacionadas y la misma cantidad de ecuaciones que incógnitas, y cómo estas ecuaciones son lineales. Además, se mencionan otros métodos de resolución como igualación, reducción y sustitución, prometiendo más detalles en futuras entregas.
Takeaways
- 📚 El vídeo trata sobre el sistema de ecuaciones lineales 2x2, que son sistemas de ecuaciones con dos incógnitas y dos ecuaciones relacionadas.
- 👩🏫 Se explica que para resolver problemas con dos incógnitas, como la edad de Esperanza y Rodrigo, se necesitan dos ecuaciones que representen ambas condiciones del problema.
- 🔢 Se menciona que las ecuaciones deben ser lineales, lo que significa que las incógnitas deben tener un exponente igual a 1 y su gráfica será una recta.
- 📈 Se destaca que un sistema de ecuaciones lineales debe tener el mismo número de ecuaciones que de incógnitas para poder resolverlo.
- 🎓 Se da un ejemplo práctico con la compra de aguacates y jitomates para ilustrar cómo se establecen las ecuaciones a partir de una situación real.
- 🛒 Se describe una situación donde Juanita compra aguacates y jitomates en dos semanas a diferentes precios, lo que lleva a un sistema de ecuaciones para determinar la cantidad comprada.
- 📉 Se menciona el método gráfico como una de las técnicas para resolver sistemas de ecuaciones lineales, aunque se indica que hay otros métodos como la igualación, reducción y sustitución.
- 👀 Se enfatiza la importancia de verificar que un sistema de ecuaciones cumpla con las características necesarias para ser considerado lineal antes de intentar resolverlo.
- 📚 El vídeo es didáctico y está dirigido a un público que ya tiene conocimientos básicos de álgebra y resolución de ecuaciones.
- 🎬 El contenido del vídeo se presenta de manera amena y se utiliza música para mejorar la experiencia de aprendizaje.
Q & A
¿Qué es un sistema de ecuaciones lineales con dos incógnitas?
-Un sistema de ecuaciones lineales con dos incógnitas es una colección de dos ecuaciones que representan relaciones entre dos variables, donde cada variable tiene un exponente igual a 1.
¿Cuáles son las características principales que debe cumplir un sistema de ecuaciones lineales para ser válido?
-Un sistema de ecuaciones lineales debe tener al menos dos ecuaciones relacionadas, cada ecuación debe representar una condición del problema, todas las incógnitas deben ser lineales (exponete 1), y debe haber el mismo número de ecuaciones que de incógnitas.
¿Cómo se determina si una ecuación es lineal?
-Una ecuación es lineal si todas las incógnitas en ella tienen un exponente igual a 1, lo que significa que su gráfica será una recta.
¿Qué métodos se pueden usar para resolver un sistema de ecuaciones lineales con dos incógnitas?
-Los métodos para resolver un sistema de ecuaciones lineales con dos incógnitas incluyen el método gráfico, el de igualación, el de reducción y el de sustitución.
¿Qué es el método gráfico para resolver un sistema de ecuaciones lineales?
-El método gráfico implica representar gráficamente cada ecuación como una recta en un plano cartesiano y encontrar el punto de intersección, si existe, que representa la solución del sistema.
¿Cuál es la relación entre la edad de Esperanza y la de su hijo Rodrigo según el ejemplo del video?
-La edad de Esperanza es el cuádruple de la edad de Rodrigo, y dentro de 12 años, la edad de Esperanza será el doble que la de Rodrigo.
¿Cómo se puede representar matemáticamente la relación de edad entre Esperanza y Rodrigo?
-Se pueden escribir dos ecuaciones: E = 4R (donde E es la edad de Esperanza y R la de Rodrigo) y E+12 = 2(R+12) para representar la relación de edad en 12 años.
¿Cuál fue el precio del kilogramo de aguacate y de jitomate la semana pasada según el ejemplo del video?
-La semana pasada, el kilogramo de aguacate estaba a 90 pesos y el kilogramo de jitomate a 10 pesos.
¿Cuánto pagó Juanita por el aguacate y el jitomate la semana pasada y esta semana según el ejemplo?
-La semana pasada, Juanita pagó 320 pesos por la misma cantidad de aguacate y jitomate que esta semana, donde pagó 240 pesos.
¿Cómo se representa matemáticamente el sistema de ecuaciones para el problema de los precios de aguacate y jitomate?
-Se pueden escribir dos ecuaciones: 90a + 10j = 320 (precios la semana pasada) y 60a + 12j = 240 (precios esta semana), donde 'a' representa los kilogramos de aguacate y 'j' los de jitomate.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

Sistemas de ecuaciones lineales 2x2 INTRODUCCIÓN
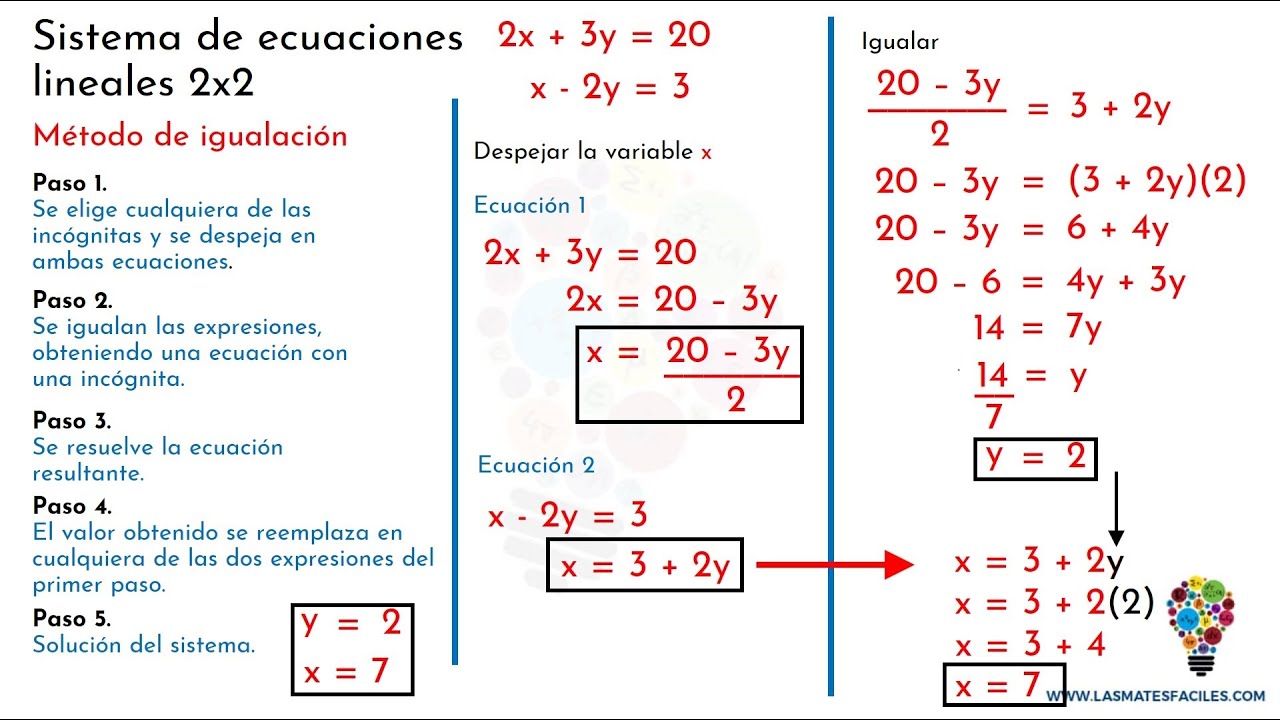
Sistemas de Ecuaciones 2x2 - Método de Igualación

✅ Sistema de Ecuaciones Lineales [ Método de Eliminación ] - Ejemplos Resueltos #1

Matemáticas Video 2 8

Sistema de ecuaciones 2x2. Método de suma y resta.Álgebra

Sistema de Ecuaciones 2x2 - Método de Eliminación o Reducción
5.0 / 5 (0 votes)
