2415 Prueba de la razón entre los lados de un triángulo 30 60 90
Summary
TLDREl video explica el triángulo 30-60-90, una figura geométrica especial. Se demuestra que si la hipotenusa tiene longitud 'x', el lado opuesto al ángulo de 30° mide 'x/2' y el lado opuesto al ángulo de 60° es '√3 * x/2'. Para ello, se utiliza un triángulo equilátero, de lado 'x', y se divide en dos triángulos 30-60-90 mediante una altitud. Se aplica el teorema de Pitágoras para encontrar la longitud del lado opuesto al ángulo de 60°, concluyendo que es '√3 * x/2'.
Takeaways
- 📐 El triángulo 30-60-90 es un tipo especial de triángulo donde los ángulos miden 30°, 60° y 90°.
- 🔍 Se utiliza el resultado de las proporciones de los lados en geometría y trigonometría.
- 📏 Si la hipotenusa tiene longitud x, el lado opuesto al ángulo de 30° mide x/2.
- 📏 El lado opuesto al ángulo de 60° mide \( \sqrt{3} \times \frac{x}{2} \).
- 🎨 Se usa un triángulo equilátero con lados de longitud x para demostrar las proporciones.
- ✂️ Al bajar una altitud desde un vértice del triángulo equilátero, se crea un ángulo recto y se divide la base en dos partes iguales.
- 🔄 Los triángulos ABD y BDC son congruentes, ya que comparten un lado (BD) y tienen dos ángulos rectos y un ángulo de 60° cada uno.
- 📉 El lado AD es igual al lado CD, y ambos miden x/2, ya que son lados de un triángulo equilátero dividido.
- 📐 Al aplicar el teorema de Pitágoras, se demuestra que el lado opuesto al ángulo de 60° es \( \sqrt{3} \times \frac{x}{2} \).
- 📘 Se concluye que en un triángulo 30-60-90, la relación de los lados es 1:√3:2, donde la hipotenusa es el lado de mayor longitud.
Q & A
¿Qué es un triángulo 30-60-90?
-Un triángulo 30-60-90 es un tipo especial de triángulo donde los ángulos miden 30 grados, 60 grados y 90 grados.
¿Cuál es la hipotenusa en un triángulo 30-60-90 si el lado opuesto al ángulo de 90 grados tiene longitud x?
-La hipotenusa en un triángulo 30-60-90 es el lado opuesto al ángulo de 90 grados, por lo tanto, si este lado tiene longitud x, la hipotenusa es x.
¿Cuál es la relación de longitud entre el lado opuesto al ángulo de 30 grados y la hipotenusa en un triángulo 30-60-90?
-El lado opuesto al ángulo de 30 grados en un triángulo 30-60-90 tiene una longitud de x/2, donde x es la longitud de la hipotenusa.
¿Cómo se calcula la longitud del lado opuesto al ángulo de 60 grados en un triángulo 30-60-90?
-La longitud del lado opuesto al ángulo de 60 grados en un triángulo 30-60-90 se calcula como √3/2 veces la longitud de la hipotenusa, es decir, √3 * (x/2).
¿Qué métodos se pueden usar para demostrar que dos triángulos son congruentes en el contexto del triángulo equilátero?
-Se pueden usar los criterios de congruencia de ángulo-lado-ángulo o lado-ángulo-lado para demostrar que dos triángulos son congruentes.
¿Cómo se demuestra que dos triángulos son congruentes en el vídeo utilizando un triángulo equilátero?
-Se demuestra que dos triángulos son congruentes al mostrar que tienen un lado común, dos ángulos rectos iguales y que los ángulos superiores también son iguales, lo que permite aplicar los criterios de congruencia.
¿Qué es la altitud en un triángulo y cómo se relaciona con el triángulo equilátero en el vídeo?
-La altitud en un triángulo es una perpendicular desde un vértice al lado opuesto. En el vídeo, al dejar caer una altitud desde un vértice del triángulo equilátero, se forma un ángulo recto y se divide la base en dos partes iguales.
¿Qué se demuestra al dividir un triángulo equilátero en dos triángulos 30-60-90?
-Al dividir un triángulo equilátero en dos triángulos 30-60-90, se demuestra que el lado opuesto al ángulo de 30 grados en un triángulo 30-60-90 es x/2, donde x es la longitud de la hipotenusa.
¿Cómo se utiliza el teorema de Pitágoras para encontrar la longitud del lado opuesto al ángulo de 60 grados en un triángulo 30-60-90?
-Se utiliza el teorema de Pitágoras (a² + b² = c²) donde a y b son los lados opuestos a los ángulos de 30 y 60 grados respectivamente, y c es la hipotenusa. Al reemplazar y simplificar, se encuentra que el lado opuesto al ángulo de 60 grados es √3 * (x/2).
¿Qué conclusiones se pueden extraer del análisis de los lados de un triángulo 30-60-90 en relación con su aplicación en geometría y trigonometría?
-Las conclusiones son que la relación de los lados en un triángulo 30-60-90 es fundamental para entender propiedades y resolver problemas en geometría y trigonometría, como se demuestra en el vídeo al analizar la relación entre la hipotenusa y los lados opuestos a los ángulos de 30 y 60 grados.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
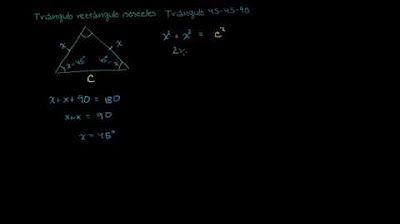
2416 Razón entre los lados de un triángulo 45 45 90
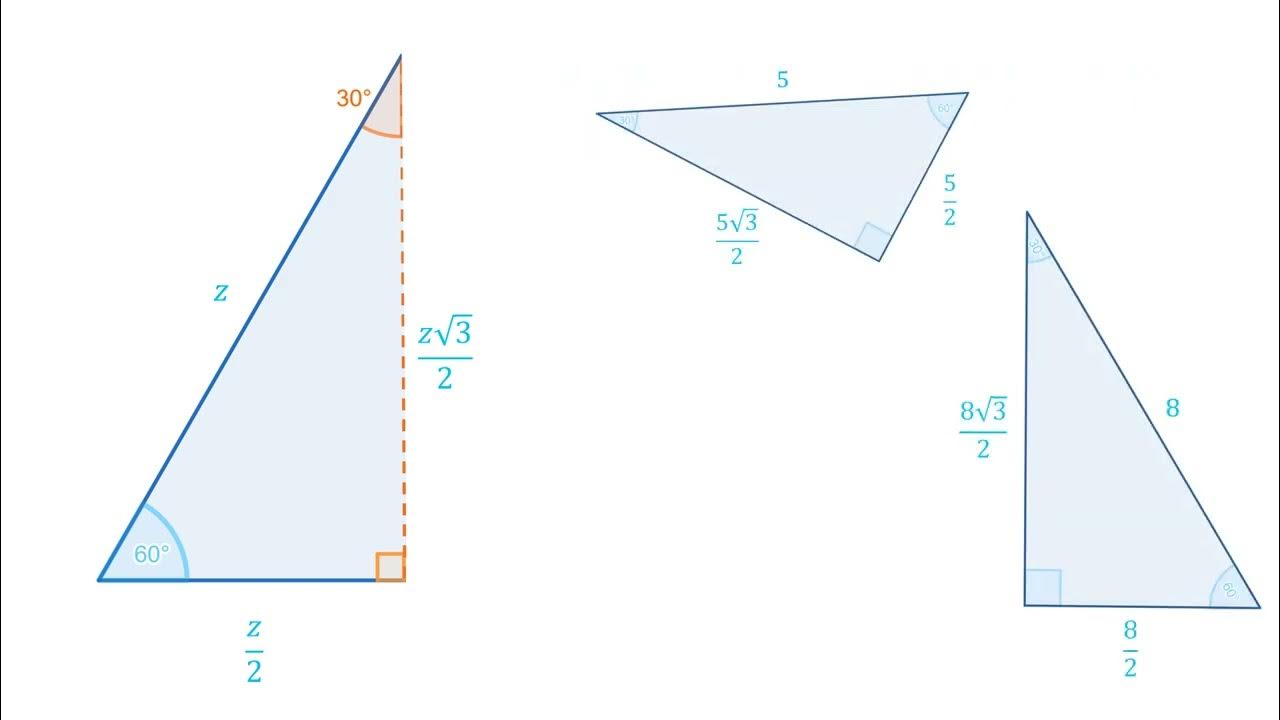
Razones Trigonométricas en Triángulos Especiales

CUERPOS DE REVOLUCION Super facil

Cómo trazar Ángulos con Escuadra y Cartabón: 15º, 75º, 45º, 60º, 30º, 90º, 165º, 105º, 135º y más.

⭐ Determinar el Valor de los Ángulos Complementarios | Video 11

Datos situación VII - Construcción de estudiantes
5.0 / 5 (0 votes)
