2416 Razón entre los lados de un triángulo 45 45 90

KhanAcademyEspañol

17 Jun 201305:44

Summary

TLDREste video educativo explica los tipos de triángulos más comunes: el triángulo de 30-60-90 y el triángulo de 45-45-90. Se describe cómo, en un triángulo de 30-60-90, los lados tienen una relación de 1:√3:2, donde la hipotenusa es el doble del lado opuesto al ángulo de 30 grados. En el triángulo de 45-45-90, los dos lados base son iguales y la hipotenusa es √2 veces la longitud de cualquier lado base. El video es una excelente herramienta para comprender las proporciones en estos triángulos y cómo aplicarlas en problemas prácticos.

Takeaways

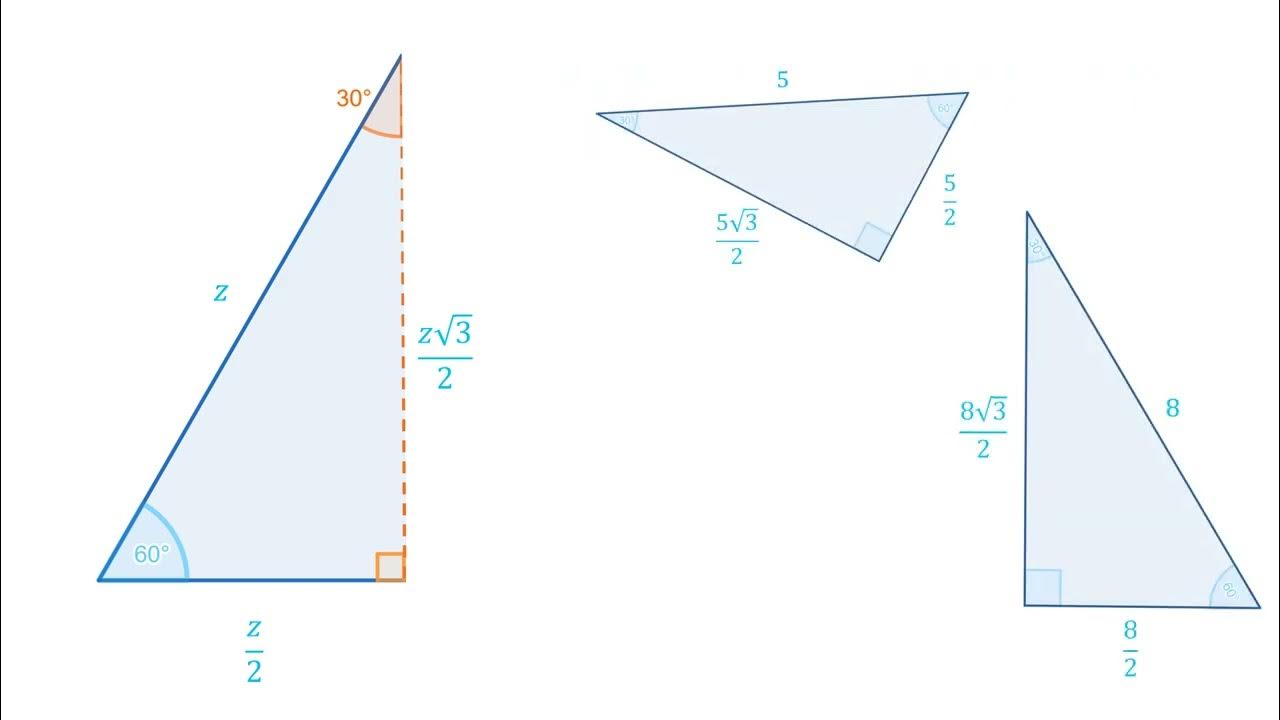
📐 En un triángulo de 30°-60°-90°, si la hipotenusa es \( x \), el lado opuesto al ángulo de 30° es \( \frac{x}{2} \) y el lado opuesto al ángulo de 60° es \( \frac{\sqrt{3}x}{2} \).
🔢 Si el lado más corto de un triángulo de 30°-60°-90° vale 1, el lado opuesto al ángulo de 60° vale \( \sqrt{3} \) y la hipotenusa es 2.
👀 Un triángulo de 30°-60°-90° puede ser reconocido por sus proporciones de 1: \( \sqrt{3} \) : 2.
📏 El triángulo de 45°-45°-90° también se conoce como triángulo rectángulo isósceles, donde dos lados son iguales y los ángulos de la base miden 45° cada uno.
🧩 En un triángulo de 45°-45°-90°, si un lado es \( x \), el otro lado también es \( x \) y la hipotenusa es \( x\sqrt{2} \).
🔄 La relación de los lados en un triángulo de 45°-45°-90° es 1:1: \( \sqrt{2} \), donde la hipotenusa es \( \sqrt{2} \) veces el largo de cualquiera de los lados iguales.
📐 El teorema de Pitágoras se aplica directamente en ambos tipos de triángulos para encontrar la hipotenusa.
📘 La identificación de un triángulo de 30°-60°-90° o 45°-45°-90° se basa en sus proporciones específicas y no en la medida exacta de los lados.
🔎 Al observar un triángulo con proporciones conocidas, se puede determinar rápidamente si es de 30°-60°-90° o 45°-45°-90° y calcular sus lados correspondientes.
📚 Los triángulos de 30°-60°-90° y 45°-45°-90° son fundamentales en matemáticas y geometría, ya que sus proporciones fijas facilitan el cálculo y la identificación.

Q & A

¿Cuál es la relación de longitudes entre los lados de un triángulo de 30-60-90?
-En un triángulo de 30-60-90, si la hipotenusa vale x, el lado opuesto al ángulo de 30 grados tiene una longitud de x/2 y el lado opuesto al ángulo de 60 grados tiene una longitud de √3 * x/2.
Si el lado más corto de un triángulo de 30-60-90 vale 1, ¿cuál es la longitud de la hipotenusa?
-Si el lado más corto vale 1, la hipotenusa, que es el doble del lado más corto, valdrá 2.
¿Qué es un triángulo de 45-45-90 y cómo se relaciona con un triángulo rectángulo isósceles?
-Un triángulo de 45-45-90 es un triángulo rectángulo que también es isósceles, lo que significa que dos de sus lados miden lo mismo y los dos ángulos de la base miden 45 grados cada uno.
¿Cómo se calcula la longitud de la hipotenusa en un triángulo de 45-45-90?
-Si los dos lados iguales de un triángulo de 45-45-90 miden x, la hipotenusa (c) se calcula como √2 * x, usando el teorema de Pitágoras.
Si un triángulo de 45-45-90 tiene un lado de 3 unidades, ¿cuál es la longitud de la hipotenusa?
-Si un lado del triángulo de 45-45-90 mide 3 unidades, la hipotenusa será 3 * √2.
¿Cuál es la relación de las longitudes de los lados en un triángulo de 45-45-90?
-En un triángulo de 45-45-90, la relación de las longitudes de los lados es 1:1:√2, donde los dos lados iguales miden 1 unidad y la hipotenusa mide √2 unidades.
¿Cómo se identifica un triángulo de 30-60-90 si se conocen las longitudes de sus lados?
-Si en un triángulo se observan longitudes de los lados que siguen la relación 1:√3:2, entonces se puede identificar como un triángulo de 30-60-90.
¿Qué método se utiliza para determinar si un triángulo es de 45-45-90 basado en sus lados?
-Para determinar si un triángulo es de 45-45-90, se verifica si los dos lados cortos miden lo mismo y si la longitud de la hipotenusa es √2 veces la longitud de cualquier lado corto.
Si se te muestra un triángulo con lados de 2, 2√3 y 4, ¿es un triángulo de 30-60-90?
-Sí, si los lados de un triángulo miden 2, 2√3 y 4, entonces se trata de un triángulo de 30-60-90, ya que las longitudes de los lados siguen la relación correcta para este tipo de triángulo.
¿Cuál es la importancia de conocer las relaciones de los lados en los triángulos de 30-60-90 y 45-45-90?
-Las relaciones de los lados en los triángulos de 30-60-90 y 45-45-90 son importantes porque permiten identificar rápidamente el tipo de triángulo y calcular la longitud de cualquier lado si se conocen las medidas de los otros.

Outlines

00:00

📐 Triángulos de 30-60-90 y 45-45-90

En el primer párrafo se explica cómo se relacionan los lados de un triángulo de 30-60-90. Se asume que la hipotenusa vale x, y se deduce que el lado opuesto al ángulo de 30 grados tiene una longitud de x/2, mientras que el lado opuesto al ángulo de 60 grados mide \( \sqrt{3} \times \frac{x}{2} \). Se ilustra con ejemplos cómo se pueden encontrar las longitudes de los lados si se conoce una de ellas. Además, se introduce el concepto de triángulo de 45-45-90, que es un triángulo rectángulo isósceles, y se explica que los dos lados iguales miden lo mismo y los ángulos de la base también son iguales, resultando en un ángulo de 45 grados para cada uno. Se utiliza el teorema de Pitágoras para encontrar la relación entre los lados y la hipotenusa, obteniendo que la hipotenusa es \( \sqrt{2} \) veces el largo del lado isósceles.

05:02

🔍 Razones de los lados en triángulos especiales

El segundo párrafo se centra en las relaciones de los lados en triángulos de 45-45-90 y 30-60-90. Se resume que para un triángulo de 45-45-90, si un lado vale 1, el otro lado también vale 1 y la hipotenusa será \( \sqrt{2} \) veces el largo de cualquiera de los lados, resultando en una relación de 1:1:\( \sqrt{2} \). Se menciona que esta relación es útil para identificar rápidamente un triángulo de 45-45-90. También se repasa que para un triángulo de 30-60-90, las relaciones son 1:√3:2. Se sugiere que estos conceptos se aplicarán en futuros videos para resolver problemas relacionados con triángulos.

Mindmap

Keywords

💡Triángulo de 30-60-90

Un triángulo de 30-60-90 es un tipo especial de triángulo rectángulo donde los ángulos son de 30 grados, 60 grados y 90 grados. En este triángulo, la relación entre los lados es fija: el lado opuesto al ángulo de 30 grados es la mitad de la hipotenusa, y el lado opuesto al ángulo de 60 grados es la mitad de la hipotenusa multiplicado por la raíz cuadrada de 3. En el guion, se usa este concepto para explicar cómo se relacionan los lados cuando se conoce la longitud de uno de ellos.

💡Hipotenusa

La hipotenusa es el lado más largo de un triángulo rectángulo, y es la línea opuesta al ángulo recto (90 grados). En el contexto del video, se menciona que en un triángulo de 30-60-90, la hipotenusa es dos veces más larga que el lado opuesto al ángulo de 30 grados, y se usa para demostrar cómo se calcula su longitud en función de los otros lados.

💡Teorema de Pitágoras

El teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados. En el guion, se aplica este teorema para encontrar la longitud de la hipotenusa en un triángulo de 45-45-90, donde los lados opuestos a los ángulos de 45 grados son iguales.

💡Triángulo de 45-45-90

Un triángulo de 45-45-90 es un triángulo isósceles con un ángulo recto, donde los dos lados opuestos a los ángulos de 45 grados son iguales. El video explica que la relación de los lados en este triángulo es 1:1:√2, donde la hipotenusa es √2 veces más larga que uno de los lados iguales.

💡Isósceles

Un triángulo isósceles es aquel en el que al menos dos lados son iguales en longitud. En el video, se usa este término para describir un triángulo de 45-45-90, donde los dos lados opuestos a los ángulos de 45 grados son iguales, y se relaciona con la forma en que se calcula la hipotenusa.

💡Razón de los lados

La razón de los lados en un triángulo se refiere a la relación de las longitudes de sus lados. En el video, se discuten las razones específicas de los lados en triángulos de 30-60-90 y 45-45-90, que son 1:√3:2 y 1:1:√2 respectivamente, y se explica cómo se pueden usar para determinar la longitud de un lado dado los otros.

💡Ángulo recto

Un ángulo recto es un ángulo de 90 grados, que se encuentra en triángulos rectángulos. El video utiliza el concepto de ángulo recto para definir triángulos de 30-60-90 y 45-45-90, y para explicar cómo se relacionan los lados en estos triángulos.

💡Raíz cuadrada

La raíz cuadrada de un número es otro número que, al multiplicarse por sí mismo, da el primer número. En el guion, se usa la raíz cuadrada para describir la relación entre los lados en triángulos de 30-60-90 y 45-45-90, especialmente en la longitud de los lados opuestos a los ángulos de 60 grados y 45 grados respectivamente.

💡Triángulo rectángulo

Un triángulo rectángulo es un triángulo que tiene un ángulo de 90 grados. El video se centra en dos tipos específicos de triángulos rectángulos: los de 30-60-90 y los de 45-45-90, explicando cómo se relacionan sus lados y cómo se pueden identificar y medir.

💡Relación fija de lados

En ciertos tipos de triángulos, como los de 30-60-90 y 45-45-90, hay una relación fija entre las longitudes de sus lados. El video explica estas relaciones y cómo se pueden usar para determinar la longitud de los lados cuando se conoce la longitud de uno de ellos, lo que es útil en problemas de trigonometría y geometría.

Highlights

En el video pasado se explicó cómo las razones de los lados de un triángulo de 30-60-90 son 1:√3:2.

Se describe cómo el lado opuesto al ángulo de 60 grados es √3 veces el lado más corto.

Se sugiere una alternativa de pensar en las proporciones de los lados si el lado más corto vale 1.

Se explica que si el lado opuesto al ángulo de 60 grados vale 1, entonces el lado opuesto al ángulo de 30 grados vale √3.

Se menciona que la hipotenusa es el doble del lado más corto en un triángulo de 30-60-90.

Se da un ejemplo práctico de cómo identificar un triángulo de 30-60-90 y sus proporciones.

Se introduce el concepto de triángulo de 45-45-90, también conocido como triángulo rectángulo isósceles.

Se explica que en un triángulo de 45-45-90, los dos lados de la base miden lo mismo y los ángulos de la base miden 45 grados cada uno.

Se demuestra matemáticamente que la suma de los ángulos en un triángulo siempre es de 180 grados.

Se aplica el teorema de Pitágoras para encontrar la relación entre los lados de un triángulo de 45-45-90.

Se concluye que la hipotenusa en un triángulo de 45-45-90 es √2 veces la longitud del lado de la base.

Se da un ejemplo de cómo calcular la hipotenusa en un triángulo de 45-45-90 cuando se conoce la longitud de un lado de la base.

Se resume que en un triángulo de 45-45-90, la proporción de los lados es 1:1:√2.

Se hace una comparación entre las proporciones de los lados en un triángulo de 30-60-90 y uno de 45-45-90.

Se sugiere aplicar estos conocimientos en futuras aplicaciones prácticas.