Math Antics - Common Denominator LCD
Summary
TLDRThis video script teaches the method of finding the 'least common denominator' (LCD) for adding unlike fractions. It explains that the LCD is the smallest common multiple of the denominators, and demonstrates how to create multiples of each denominator to find this common multiple. The script provides step-by-step examples, such as adding 3/8 and 5/24, showing how to adjust fractions to a common denominator using 'whole fractions' derived from the multiples chart. It emphasizes the importance of practice to master the technique, inviting viewers to engage with the material on www.mathantics.com.
Takeaways
- 📚 The 'easiest common denominator' is a preferred method for simplifying fractions, but there are cases where a different method is better.
- 🔢 When one fraction's denominator is a multiple of another, it's more efficient to use a different method to find a common denominator.
- 👨🏫 The 'least common denominator' (LCD) method is sometimes required by teachers, and it involves finding the smallest common multiple of the denominators.
- 📈 To find the LCD, list multiples of each denominator until a common multiple is found, which is the least common multiple (LCM).
- 📋 Organizing multiples in a table helps in identifying the LCM and keeping track of the process.
- 🔑 The LCM becomes the new common denominator for converting unlike fractions into equivalent fractions with the same denominator.
- 📝 Determine the 'whole fractions' needed to convert the original fractions to those with the common denominator by using the multipliers that resulted in the LCM.
- 🌰 For example, if multiplying the first fraction's denominator by 4 gives the LCM, then use 4/4 as the 'whole fraction' for conversion.
- 📉 If the second fraction's denominator is already the LCM, multiplying by 1 (or not multiplying at all) is sufficient.
- ➕ Once the fractions are converted to have the same denominator, they can be added using the standard addition procedure for fractions.
- 📚 The script provides step-by-step examples to illustrate the process of finding the LCD and converting fractions, emphasizing practice for mastery.
Q & A
What is the 'easiest common denominator' mentioned in the script?
-The 'easiest common denominator' refers to the product of the denominators of the unlike fractions, which is a quick and easy method to find a common denominator for adding or comparing fractions.
Why might someone prefer the 'easiest common denominator' method?
-The 'easiest common denominator' method is preferred because it is quick, easy to remember, and straightforward to apply when adding or comparing fractions.
Under what circumstances should the 'least common denominator' method be used instead of the 'easiest common denominator'?
-The 'least common denominator' method should be used when one of the fraction's denominators is a multiple of the other, or when instructed to do so by a teacher.
What is the difference between the 'easiest common denominator' and the 'least common denominator'?
-The 'easiest common denominator' is the product of the two denominators, while the 'least common denominator' is the smallest common multiple of the two denominators.
What is a 'multiple' of a number as described in the script?
-A 'multiple' of a number is the result of multiplying that number by another whole number, such as 1, 2, 3, etc.
How do you find the 'least common multiple' of two numbers?
-To find the 'least common multiple', you list multiples of each number and identify the smallest multiple that appears in both lists.
What is the purpose of arranging multiples in a table when finding the 'least common denominator'?
-Arranging multiples in a table helps to keep the multiples organized and makes it easier to identify the least common multiple.
How do you determine the 'whole fractions' needed to convert unlike fractions to equivalent fractions with the 'least common denominator'?
-The 'whole fractions' are determined by the multiples used to reach the least common multiple for each original fraction.
In the example with fractions 3/8 and 5/24, what is the least common multiple of 8 and 24?
-The least common multiple of 8 and 24 is 24, as it is the smallest number that appears in both multiples lists.
What is the least common denominator for the fractions 2/9 and 7/12 as given in the script?
-The least common denominator for the fractions 2/9 and 7/12 is 36, as it is the smallest common multiple of 9 and 12.
How can practicing exercises help in understanding the 'least common denominator' method?
-Practicing exercises allows learners to apply the method in various scenarios, reinforcing their understanding and making the process second nature.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

Subtracting Fractions with Unlike Denominators | Math with Mr. J

Le quattro operazioni fondamentali con le frazioni

MATEMATIKA 6 SD VIDEO 008 PENJUMLAHAN DAN PENGURANGAN PECAHAN

Addition and Subtraction of Rational Numbers - Operation on Rational Numbers

Addition and Subtraction of Rational Algebraic Expressions I Señor Pablo TV
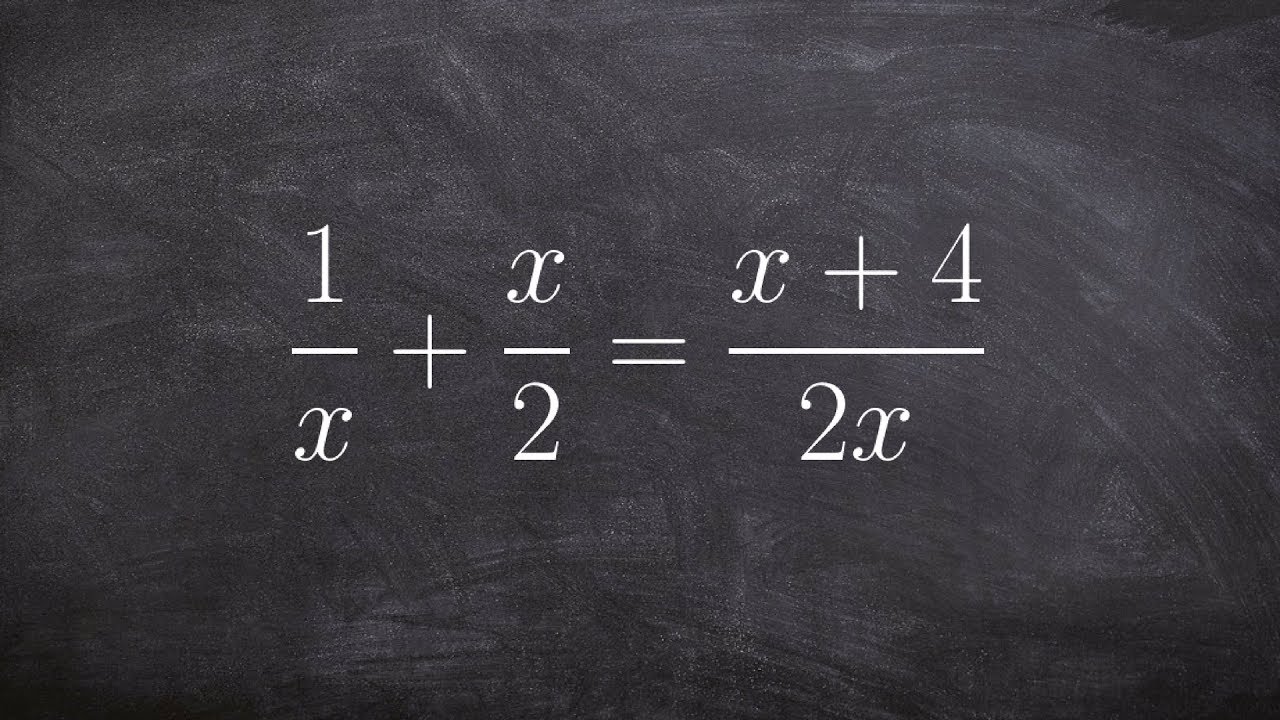
Solving a rational Equation
5.0 / 5 (0 votes)
