CIRCLES || PRE-CALCULUS
Summary
TLDRThis video lesson offers an in-depth exploration of circles, beginning with an overview of conic sections and their formation. It defines a circle as the set of points equidistant from a central point, known as the center, and introduces the concept of the radius. The lesson then delves into the standard form of a circle's equation, providing several examples to illustrate how to derive the equation from a given center and radius. The examples cover a range of scenarios, including circles centered at the origin and those with non-integer radii, concluding with a reminder to like, subscribe, and stay tuned for more educational content.
Takeaways
- 📚 The lesson is about the concept of circles within the broader topic of conic sections.
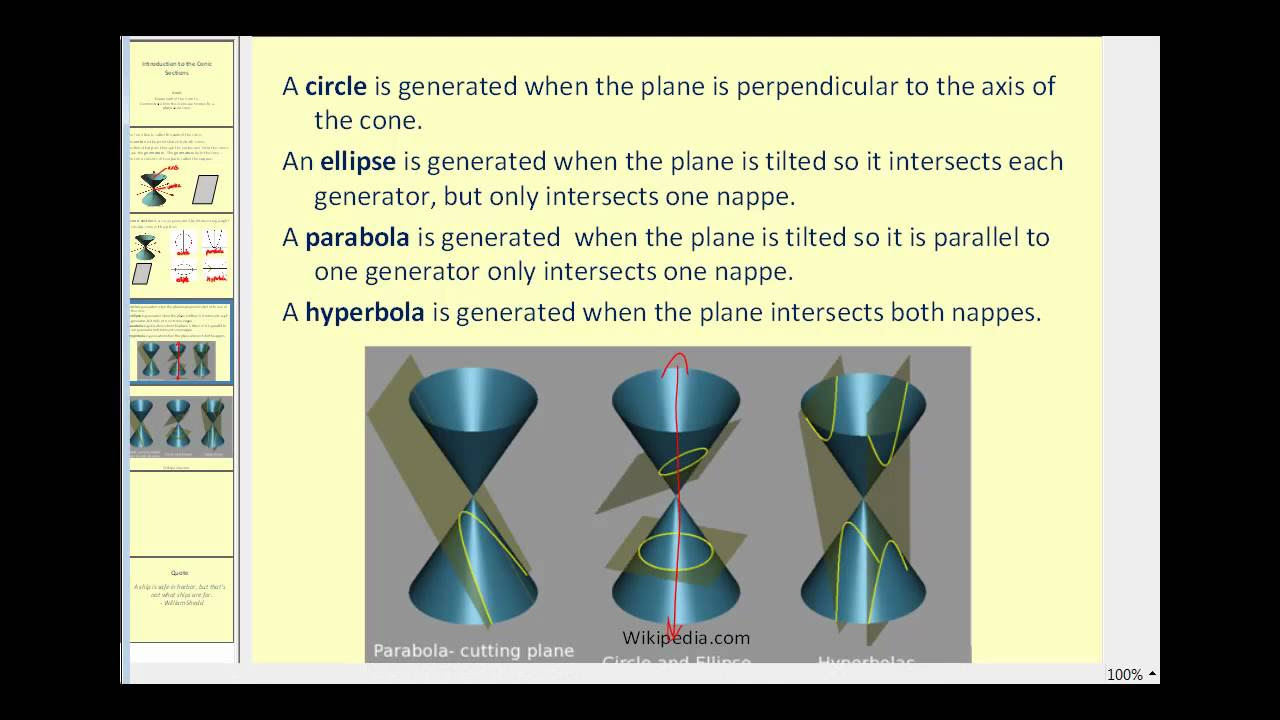
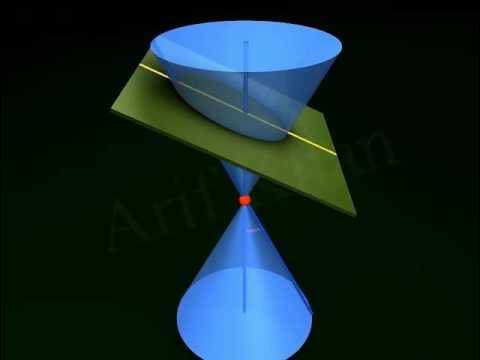
- 📐 Conic sections are formed by the intersection of a plane and a cone at different angles, resulting in four types of conic sections.
- ⭕ A circle is defined as a set of points equidistant from a fixed point, known as the center.
- 📏 The constant distance from the center to any point on the circle is the radius.
- 🔢 The standard form of a circle's equation is \( (x-h)^2 + (y-k)^2 = r^2 \), where \( (h, k) \) is the center and \( r \) is the radius.
- 📈 The video demonstrates how to find the equation of a circle given the center and radius, using the standard form.
- 📝 Examples are provided to illustrate the process of writing the equation of a circle with various centers and radii.
- 🔍 The script includes examples with centers at the origin, as well as with non-zero coordinates, and varying radii.
- 🧩 The importance of understanding the relationship between the center coordinates, radius, and the equation of a circle is emphasized.
- 📉 The video covers cases where the radius is given as a whole number, as well as when it is expressed as a square root.
- 💡 The lesson concludes with a reminder to like, subscribe, and hit the bell for more educational content.
Q & A
What is a conic section?
-A conic section is the intersection of a plane and a cone, which can produce four different types of conic sections depending on the angle at which the plane slices the cone.
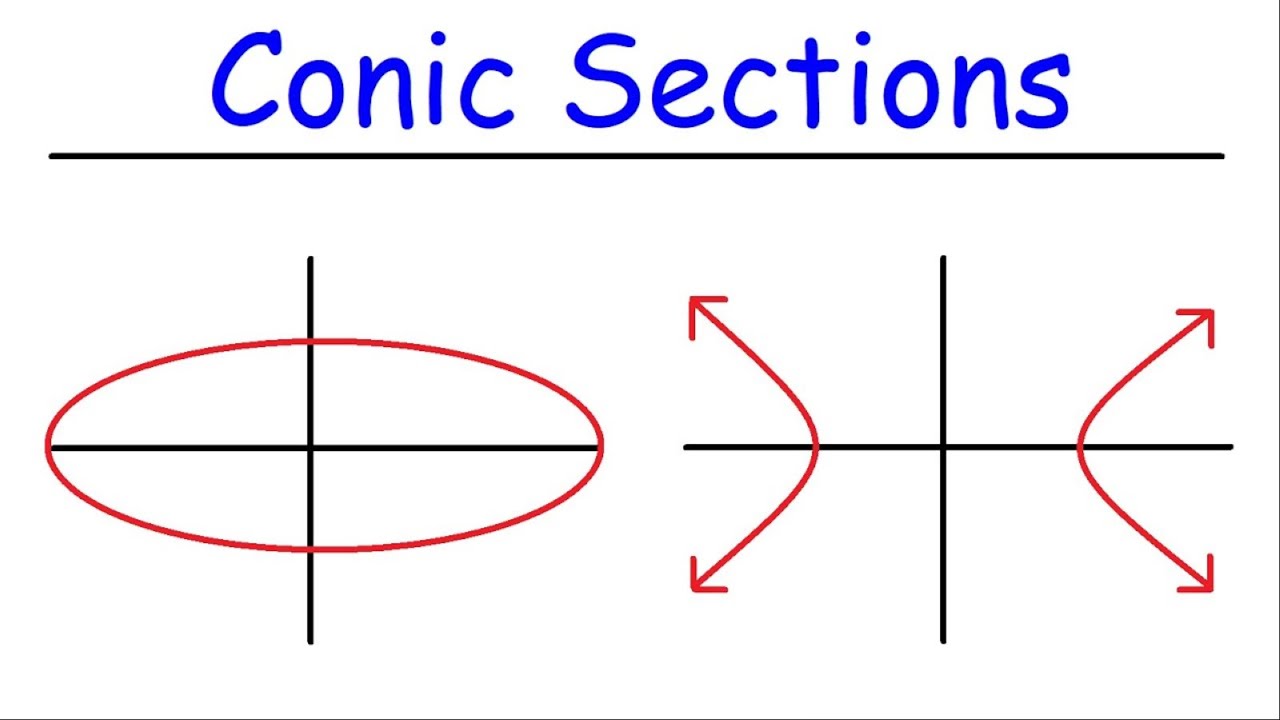
What are the four types of conic sections?
-The script does not specify the four types of conic sections, but they are typically a circle, ellipse, parabola, and hyperbola.
What is the definition of a circle in the context of this script?
-A circle is defined as the set of all points on a plane equidistant from a fixed point, known as the center.
What is the standard form of the equation of a circle?
-The standard form of the equation of a circle is (x - h)² + (y - k)² = r², where (h, k) is the center of the circle and r is the radius.
How do you find the equation of a circle with a center at the origin and a radius of 5 units?
-The equation of a circle with a center at the origin (0, 0) and a radius of 5 units is x² + y² = 25.
What is the equation of a circle centered at (0, 3) with a radius of 6 units?
-The equation of a circle centered at (0, 3) with a radius of 6 units is x² + (y - 3)² = 36.
If the center of a circle is at (2, -5) and the radius is 10, what is the equation of the circle?
-The equation of a circle with a center at (2, -5) and a radius of 10 is (x - 2)² + (y + 5)² = 100.
What is the equation of a circle with a center at (1, 5) and a radius of √17 units?
-The equation of a circle with a center at (1, 5) and a radius of √17 units is (x - 1)² + (y - 5)² = 17.
How do you find the equation of a circle with a center at (0, 0) and a radius of 8 units?
-The equation of a circle with a center at the origin and a radius of 8 units is x² + y² = 64.
What is the equation of a circle with a center at (-7, 5) and a radius of 2√14 units?
-The equation of a circle with a center at (-7, 5) and a radius of 2√14 units is (x + 7)² + (y - 5)² = (2√14)².
What is the process to write the equation of a circle given its center and radius?
-To write the equation of a circle given its center (h, k) and radius r, you use the formula (x - h)² + (y - k)² = r², substituting the actual values of h, k, and r.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード5.0 / 5 (0 votes)