Componentes Rectangulares de un vector | Ejemplo 2
Summary
TLDREn este curso de vectores, se enseña cómo encontrar las componentes rectangulares de un vector. Se compara el plano de coordenadas geográficas con el plano cartesiano y se utiliza un gráfico para verificar los resultados. Se explican las fórmulas para calcular las componentes x e y, y se ejemplifican con ángulos de 20 y 45 grados. Al final, se invita a los estudiantes a practicar con ejercicios adicionales.
Takeaways
- 😀 El curso trata sobre vectores y cómo encontrar sus componentes rectangulares.
- 🏫 En este segundo vídeo se avanza más rápido, asumiendo conocimientos previos del primer vídeo.
- 📚 Se recomienda ver el primer vídeo para entender las bases antes de seguir con este.
- 📐 Al comparar el plano de coordenadas geográficas con el plano cartesiano, el este es positivo en el plano cartesiano y el oeste es negativo.
- 🧭 Al norte se asocia el positivo del eje Y y al sur el negativo, lo que ayuda a determinar las componentes de un vector.
- 📈 Se sugiere graficar el vector para verificar la precisión de las componentes rectangulares encontradas.
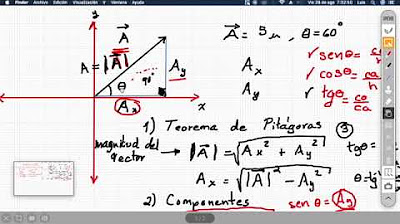
- 🔢 Las componentes rectangulares se calculan usando la magnitud del vector y los trigonómetros del ángulo correspondiente: componente X = magnitud * coseno(ángulo), componente Y = magnitud * seno(ángulo).
- 📉 La componente X es negativa cuando el vector apunta hacia el oeste y la componente Y es positiva cuando apunta hacia el norte.
- 📚 Se enfatiza la importancia de realizar ejercicios para practicar la determinación de componentes rectangulares de vectores.
- 📚 Se proporciona un ejemplo de cómo calcular las componentes rectangulares de un vector dado su dirección y magnitud.
- 👋 El instructor invita a los estudiantes a suscribirse, comentar, compartir y dar like al video para continuar aprendiendo sobre vectores.
Q & A
¿Qué es lo primero que se debe observar para encontrar las componentes rectangulares de un vector?
-Lo primero que se debe observar es la dirección del vector en relación con los puntos cardinales y cómo se compara con el plano cartesiano. Este análisis ayuda a determinar si las componentes x e y son positivas o negativas.
¿Cómo se relacionan los puntos cardinales con el plano cartesiano en términos de direcciones?
-El este es positivo en el plano cartesiano, similar al eje x, mientras que el oeste es negativo. Norte es positivo en el eje y y sur es negativo, lo que corresponde a direcciones hacia arriba y hacia abajo respectivamente.
¿Qué es lo que se debe hacer para graficar un vector y verificar sus componentes rectangulares?
-Se debe graficar el vector en un plano de coordenadas, marcando la dirección y el ángulo con respecto al eje x y y, y luego trazar la línea que representa el vector. Esto ayuda a verificar si las componentes x e y están correctamente calculadas.
¿Cómo se calcula la componente x de un vector?
-La componente x se calcula multiplicando la magnitud del vector por el coseno del ángulo correspondiente, teniendo en cuenta que si el ángulo comienza desde el oeste, la componente x será negativa.
¿Cómo se calcula la componente y de un vector?
-La componente y se calcula multiplicando la magnitud del vector por el seno del ángulo correspondiente. Si el ángulo comienza desde el norte, la componente y será positiva.
¿Qué unidades se deben usar para las operaciones de multiplicación en la calculadora?
-Se deben usar las mismas unidades que se indican para la magnitud del vector. Por ejemplo, si el vector se mide en metros, las operaciones se realizan en metros.
¿Qué es importante tener en cuenta al graficar un vector para verificar sus componentes rectangulares?
-Es importante verificar que la componente x sea más larga que la componente y si la dirección del vector es correcta, lo cual indica que las componentes están calculadas correctamente.
¿Cómo se relaciona el ángulo de 20 grados con las componentes rectangulares del vector?
-El ángulo de 20 grados indica la dirección en la que se debe graficar el vector. La componente x se calcula con el coseno de este ángulo y la componente y con el seno, considerando las convenciones de signo para las direcciones.
¿Qué ocurre si el ángulo comienza con 'sur' en lugar de 'norte'?
-Si el ángulo comienza con 'sur', se debe considerar el ángulo opuesto, que sería 180 grados menos el ángulo original, para calcular las componentes rectangulares correctamente.
¿Cómo se pueden verificar las componentes rectangulares de un vector utilizando un gráfico?
-Se puede verificar graficando el vector y observando la relación entre la magnitud del vector y las direcciones de las componentes x e y. Esto ayuda a confirmar si las componentes están calculadas correctamente.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード5.0 / 5 (0 votes)